Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Không gian mẫu là tập hợp số chấm xuất hiện khi gieo con xúc xắc hai lần liên tiếp khi đó \(n\left( \Omega \right) = 6.6 = 36\)
A = {(1; 1); (1; 2); (1; 3); (1; 4); (1; 5); (1; 6)} \( \Rightarrow P\left( A \right) = \frac{6}{{36}} = \frac{1}{6}\)
B = {(1; 2); (2; 2); (3; 2); (4; 2); (5; 2); (6; 2)} \( \Rightarrow P\left( B \right) = \frac{6}{{36}} = \frac{1}{6}\)
C = {(2; 6); (3; 5); (4; 4); (5; 3); (6; 2)} \( \Rightarrow P\left( C \right) = \frac{5}{{36}}\)
D = {(1; 6); (2; 5); (3; 4); (4; 3); (5; 2); (6; 1)} \( \Rightarrow P\left( D \right) = \frac{6}{{36}} = \frac{1}{6}\)
Do đó
\(P\left( A \right).P\left( C \right) = \frac{1}{6}.\frac{5}{{36}} = \frac{5}{{216}};P\left( B \right).P\left( C \right) = \frac{1}{6}.\frac{5}{{36}} = \frac{5}{{216}};P\left( C \right).P\left( D \right) = \frac{5}{{36}}.\frac{1}{6} = \frac{5}{{216}}\)
Mặt khác
AC = \(\emptyset \Rightarrow P\left( {AC} \right) = 0\)
BC = {(6; 2)} \( \Rightarrow P\left( {BC} \right) = \frac{1}{{36}}\)
CD = \(\emptyset \Rightarrow P\left( {CD} \right) = 0\)
Khi đó \(P\left( {AC} \right) \ne P\left( A \right).P\left( C \right);P\left( {BC} \right) \ne P\left( B \right).P\left( C \right);P\left( {CD} \right) \ne P\left( C \right).P\left( D \right)\)
Vậy các cặp biến cố A và C; B và C, C và D không độc lập.

Đáp án B
Phương pháp:
Phương trình a x 2 + b x + c = 0 ( a ≠ 0 ) có nghiệm
⇔ ∆ ≥ 0

![]()
![]()
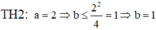
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Gọi A là biến cố:
"Phương trình a x 2 + b x + c = 0 có nghiệm"
![]()
![]()

Xác suất:
a. \(\dfrac{3}{6}.\dfrac{3}{6}=\dfrac{1}{4}\)
b. \(\dfrac{6}{36}=\dfrac{1}{6}\)
c. Xác suất mặt 6 chấm ko xuất hiện lần nào: \(\dfrac{5}{6}.\dfrac{5}{6}=\dfrac{25}{36}\)
Xác suất mặt 6 xuất hiện ít nhất 1 lần: \(1-\dfrac{25}{36}=\dfrac{11}{36}\)
d. Các trường hợp tổng 2 mặt lớn hơn hoặc bằng 10: (6;4), (4;6); (5;5); (5;6);(6;5);(6;6) có 6 khả năng
\(\Rightarrow36-6=30\) khả năng tổng số chấm bé hơn 10
Xác suất: \(\dfrac{30}{36}=\dfrac{5}{6}\)

Chọn B
Gọi Ai : “lần gieo thứ i xuất hiện mặt 6 chấm.”, với ![]()
⇒ ![]()
⇒ ![]()
A : “mặt có 6 chấm chỉ xuất hiện trong lần gieo thứ 3”
![]()
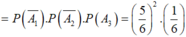


Không gian mẫu: \(6.6=36\)
a.
Lần thứ nhất có 1 khả năng thỏa mãn (3 chấm)
Lần thứ 2 bất kì => có 6 khả năng
\(\Rightarrow1.6=6\) khả năng để lần thứ nhất xuất hiện mặt 3 chấm
Xác suất: \(P=\dfrac{6}{36}=\dfrac{1}{6}\)
b.
Xác suất để cả 2 lần đều ko xuất hiện mặt 2 chấm là: \(\dfrac{5}{6}.\dfrac{5}{6}=\dfrac{25}{36}\)
Xác suất để ít nhất 1 lần xuất hiện mặt 2 chấm: \(1-\dfrac{25}{36}=\dfrac{11}{36}\)
c.
Các trường hợp có số chấm thuận lợi: (1;1);(1;2);(1;3);(1;4);(2;1);(2;2);(2;3);(3;1);(3;2);(4;1) có 10 trường hợp
Xác suất: \(P=\dfrac{10}{36}=\dfrac{5}{18}\)
Thầy có thể giải thích hơn về câu a và câu b của bài này được không ạ?

Không gian mẫu: 36
Có 2 trường hợp mặt thứ 2 xuất hiện số chấm lớn hơn 4 (5 và 6)
Do đó xác suất: \(P=\dfrac{2.6}{36}=\dfrac{1}{3}\)

Đáp án A.
Xác suất một lần gieo được mặt một chấm là ![]() Xác suất để cả ba lần không gieo được mặt một chấm là
Xác suất để cả ba lần không gieo được mặt một chấm là 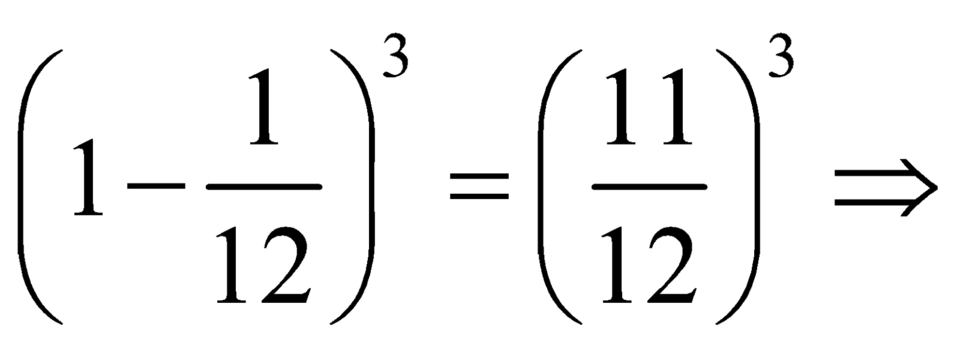 Xác suất để có ít nhất một lần gieo được mặt một chấm trong ba lượt gieo là:
Xác suất để có ít nhất một lần gieo được mặt một chấm trong ba lượt gieo là: 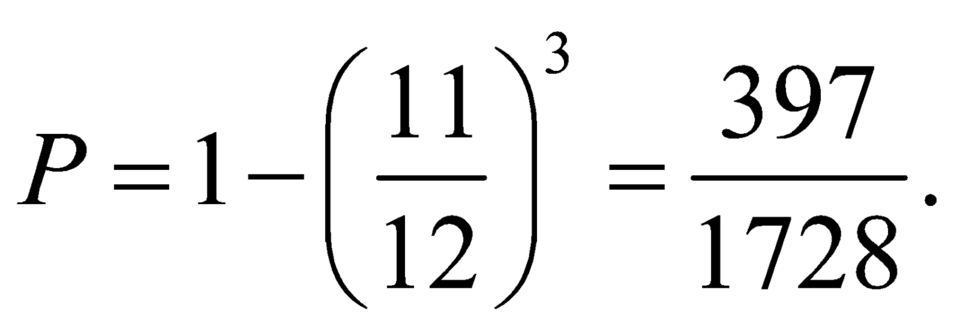

Đáp án A
Số phần tử của không gian mẫu: ![]()
Gọi A là biến cố mặt 6 chấm không xuất hiện.
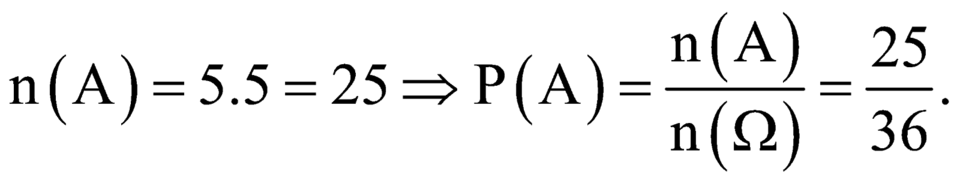
Để tính xác suất có đúng một lần xuất hiện mặt 6 chấm khi gieo con xúc xắc 2 lần liên tiếp, chúng ta cần phân tích từng khả năng có mặt 6 chấm trong 2 lần gieo.
Mỗi lần gieo con xúc xắc có 6 mặt, trong đó chỉ có một mặt có 6 chấm. Do đó, xác suất xuất hiện mặt 6 chấm trong mỗi lần gieo là \(\frac{1}{6}\), và xác suất không xuất hiện mặt 6 chấm là \(\frac{5}{6}\).
Bây giờ, chúng ta cần tính xác suất để trong 2 lần gieo có đúng một lần xuất hiện mặt 6 chấm. Điều này có thể xảy ra theo hai cách:
Xác suất cho trường hợp 1:
Do đó, xác suất cho trường hợp này là:
\(\frac{1}{6} \times \frac{5}{6} = \frac{5}{36}\)
Xác suất cho trường hợp 2:
Do đó, xác suất cho trường hợp này là:
\(\frac{5}{6} \times \frac{1}{6} = \frac{5}{36}\)
Tổng xác suất: Tổng xác suất có đúng một lần xuất hiện mặt 6 chấm trong 2 lần gieo là tổng của xác suất cho hai trường hợp trên:
\(\frac{5}{36} + \frac{5}{36} = \frac{10}{36} = \frac{5}{18}\)
Vậy xác suất để trong 2 lần gieo có đúng 1 lần xuất hiện mặt 6 chấm là \(\frac{5}{18}\).