Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

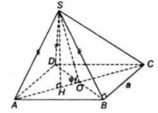
a) Tam giác ABD có AB = AD ( do ABCD là hình thoi)
=> Tam giác ABD cân tại A. Lại có góc A= 60o
=> Tam giác ABD đều.
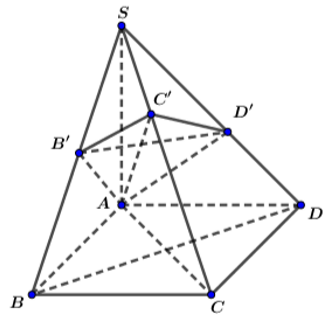
Lại có; SA = SB = SD nên hình chóp S.ABD là hình chóp đều.
* Gọi H là tâm của tam giác ABD
=>SH ⊥ (ABD)
*Gọi O là giao điểm của AC và BD.
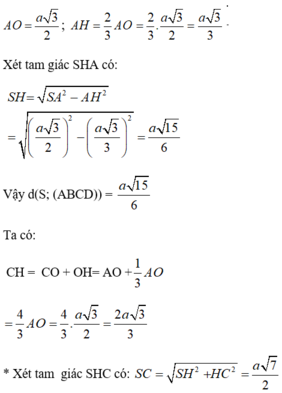


Chọn A.

Xác định được
![]()
Vì M là trung điểm SA nên
![]()
Kẻ AK ⊥ DM và chứng minh được AK ⊥ (CDM) nên
![]()
Trong tam giác vuông MAD tính được
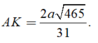

Đáp án C
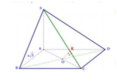
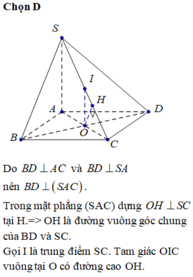
Gọi O = AC ∩ BD Kẻ OK ⊥ SC Do BD ⊥ (SAC) =>BD ⊥ OK
Do đó d(BC;SC) =OK= a 3 2
∆ S A C đ ồ n g d ạ n g ∆ O K C ( g - g )
⇒ S A O K = S C O C ⇔ x a 3 2 = x 2 + 12 a 2 a 3
⇒ x 2 = 6 a 2 ⇒ x = a 6 ⇔ S A = a 6
Khi đó: Kẻ AH ⊥ SD => AH ⊥ (SDC) => AH =d(A;(SCD))
Lại có AB//CD => AB //(SCD) => d(B;(SCD))= d(A;(SCD)=AH
∆ S A D vuông tại A có 1 A H 2 = 1 A S 2 + 1 A D 2 ⇒ A H = a 2

S A B C D H O M N P Q K E I
a/
Ta có
\(CB\perp AB\) (ABCD là hình vuông)
\(SA\perp\left(ABCD\right)\Rightarrow SA\perp CB\)
\(\Rightarrow CB\perp\left(SAB\right)\) => CB=a là khoảng cách từ C đến mp (SAB)
b/
Trong mp (SAD) dựng đường thẳng vuông góc với SD cắt SD tại H
Ta có
\(CD\perp AD\) (ABCD là hình vuông)
\(SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\)
\(\Rightarrow CD\perp\left(SAD\right)\Rightarrow CD\perp AH\)
Mà \(AH\perp SD\)
\(\Rightarrow AH\perp\left(SCD\right)\) => AH là khoảng cách từ A đến mp (SCD)
Xét tg vuông SAD có
\(SD=\sqrt{SA^2+AD^2}=\sqrt{2a^2+a^2}=a\sqrt{3}\) (Pitago)
Ta có
\(AD^2=DH.SD\) (trong tg vuông bình phương 1 cạnh góc vuông bằng tích giữa hình chiếu cạnh góc vuông đó trên cạnh huyền với cạnh huyền)
\(\Rightarrow DH=\dfrac{AD^2}{SD}=\dfrac{a^2}{a\sqrt{3}}=\dfrac{a\sqrt{3}}{3}\)
Xét tg vuông ADH có
\(AH=\sqrt{AD^2-DH^2}\) (Pitago)
\(\Rightarrow AH=\sqrt{a^2-\dfrac{a^2}{3}}=\dfrac{a\sqrt{6}}{3}\)
c/ Trong mp (ABCD) Qua O dựng đường thẳng //CD cắt AD tại M và BC tại N => MN//CD (1)
Trong mp (SAD) dựng đường thẳng // AH cắt SD tại Q => MQ // AH
TRong mp (SCD) qua Q dựng đường thẳng //CD cắt SC tại P => QP // CD (2)
Từ (1) và (2) => MN // PQ => M; N; P; Q cùng thuộc 1 mặt phẳng
=> PQ là giao tuyến của mp (MNQP) với mp (SCD)
Trong mp (MNQP) qua O dựng đường thẳng // với MQ cắt QP tại K
Ta có
MQ//AH; OH// MQ => OK//AH
Mà \(AH\perp\left(SCD\right)\)
\(\Rightarrow OK\perp\left(SCD\right)\) => OK là khoảng cách từ O đến mp (SCD)
Xét tứ giác MQKO có
MQ//OK; QP//MN => MQKO là hình bình hành => OK = MQ
Xét tg ACD có
OA=OC (t/c đường chéo hình vuông)
MO//CD
=> MA=MD (trong tg đường thẳng đi qua trung điểm của 1 cạnh // với cạnh thứ 2 thì đi qua trung điểm cạnh còn lai)
Xét tg ADH có
MA=MD (cmt); MQ//AH => QD = QH (trong tg đường thẳng đi qua trung điểm của 1 cạnh // với cạnh thứ 2 thì đi qua trung điểm cạnh còn lai)
=> MQ là đường trung bình của tg ADH
\(\Rightarrow OK=MQ=\dfrac{AH}{2}=\dfrac{1}{2}.\dfrac{a\sqrt{6}}{3}=\dfrac{a\sqrt{6}}{6}\)
d/
Trong mp (SCD) qua H dựng đường thẳng //CD cắt SC tại E => HE//CD
Ta có
AB // CD (Hai cạnh đối hình vuông)
HE // CD
=> AB//HE => A; B; H; E cùng thuộc một mặt phẳng
Trong mp (AHEB) qua e Dựng đường thẳng // AH cắt AB tại I
Ta có
AH//IE; AB//HE => AHEB là hình bình hành => IE=AH
Ta có
\(SA\perp\left(ABCD\right)\Rightarrow SA\perp AB\)
\(AB\perp AD\) (ABCD là hình vuông)
=> \(AB\perp\left(SAD\right)\Rightarrow AB\perp AH\)
Mà AH//IE
\(\Rightarrow AB\perp IE\) (1)
Ta có
\(AH\perp\left(SCD\right)\) (cmt); mà AH//IE \(\Rightarrow IE\perp\left(SCD\right)\Rightarrow IE\perp SC\) (2)
Từ (1) và (2) => IE là khoảng cách giữa AB và SC
\(\Rightarrow IE=AH=\dfrac{a\sqrt{6}}{3}\)

a/ Ta có: \(SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\)
Mà \(BD\perp AC\) (hai đường chéo hình thoi)
\(\Rightarrow BD\perp\left(SAC\right)\)
c/ Do \(SA\perp\left(ABCD\right)\Rightarrow AC\) là hình chiếu của SC lên (ABCD)
\(\Rightarrow\widehat{SCA}\) là góc giữa SC và (ABCD)
\(\widehat{ABC}=60^0\Rightarrow\Delta ABC\) đều \(\Rightarrow AC=a\)
\(tan\widehat{SCA}=\frac{SA}{AC}=\frac{a\sqrt{3}}{a}=\sqrt{3}\)
\(\Rightarrow\widehat{SCA}=60^0\)

a) Ta có:
\(\begin{array}{l}\left. \begin{array}{l}SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AB\\AB \bot A{\rm{D}}\end{array} \right\} \Rightarrow AB \bot \left( {SA{\rm{D}}} \right)\\ \Rightarrow d\left( {B,\left( {SA{\rm{D}}} \right)} \right) = AB = a\end{array}\)
b) Kẻ \(AH \bot SC \Rightarrow d\left( {A,SC} \right) = AH\)
Tam giác \(ABC\) vuông tại \(B\)\( \Rightarrow AC = \sqrt {A{B^2} + B{C^2}} = a\sqrt 2 \)
Tam giác \(SAC\) vuông tại \(A\)\( \Rightarrow SC = \sqrt {S{A^2} + A{C^2}} = a\sqrt 3 \)
Tam giác \(SAC\) vuông tại \(A\) có đường cao \(AH\)\( \Rightarrow AH = \frac{{SA.AC}}{{SC}} = \frac{{a\sqrt 6 }}{3}\)
Vậy \(d\left( {A,SC} \right) = \frac{{a\sqrt 6 }}{3}\).



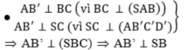



1. Xác định các đường thẳng và mặt phẳng liên quan:
2. Dựng đường thẳng song song với SC:
3. Xác định mặt phẳng chứa đường thẳng song song:
4. Tính khoảng cách:
5. Kết luận:
Lưu ý: Việc dựng đường thẳng song song giúp chuyển việc tính khoảng cách giữa hai đường thẳng chéo nhau về việc tính khoảng cách từ một điểm đến một mặt phẳng, điều này thường dễ dàng hơn.