Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phần góc giữa 2 mặt phẳng tui chưa học đến nên chưa làm được đoạn cuối phần b, bạn thông cảm nha!


a.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\CD\perp AD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\)
Mà \(CD=\left(SCD\right)\cap\left(ABCD\right)\)
\(\Rightarrow\widehat{SDA}\) là góc giữa (SCD) và (ABCD)
\(tan\widehat{SDA}=\dfrac{SA}{AD}=\sqrt{3}\Rightarrow\widehat{SDA}=60^0\)
b.
Gọi E là giao điểm AC và DI
I là trung điểm AB \(\Rightarrow AI=\dfrac{1}{2}AB=a\Rightarrow AI=DC\)
\(\Rightarrow AICD\) là hình bình hành
Mà \(\widehat{A}=90^0\Rightarrow AICD\) là hình chữ nhật
\(AI=AD=a\) (hai cạnh kề bằng nhau) \(\Rightarrow AICD\) là hình vuông
\(\Rightarrow AC\perp DI\) tại E
Lại có \(SA\perp\left(ABCD\right)\Rightarrow SA\perp DI\Rightarrow DI\perp\left(SAE\right)\)
Mà \(DI=\left(SDI\right)\cap\left(ABCD\right)\Rightarrow\widehat{SEA}\) là góc giữa (SDI) và (ABCD)
\(AE=\dfrac{1}{2}AC=\dfrac{1}{2}\sqrt{AD^2+CD^2}=\dfrac{a\sqrt{2}}{2}\)
\(\Rightarrow tan\widehat{SEA}=\dfrac{SA}{AE}=\dfrac{\sqrt{6}}{2}\Rightarrow\widehat{SEA}\approx50^046'\)

Chọn A.

Xác định được
![]()
Vì M là trung điểm SA nên
![]()
Kẻ AK ⊥ DM và chứng minh được AK ⊥ (CDM) nên
![]()
Trong tam giác vuông MAD tính được
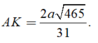

Đáp án A
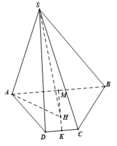
∆ DCM là tam giác đều cạnh a
=> SH ⊥ (ABCD) với H là tâm của ∆ DCM
Do đó (SA;(ABCD)) ![]()

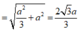
![]()
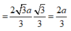
![]()
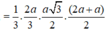
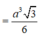


Ta có \(\frac{d\left(A,\left(SCD\right)\right)}{d\left(M,\left(SCD\right)\right)}=2\Rightarrow d=\left(m,\left(SCD\right)\right)=\frac{1}{2}d\left(A,\left(SCD\right)\right)\)
Dễ thấy AC _|_ CD, SA _|_ CD dựng AH _|_ SA => AH _|_ (SCD)
Vậy d(A,(SCD))=AH
Xét tam giác vuông SAC (A=1v) có \(\frac{1}{AH^2}=\frac{1}{AC^2}+\frac{1}{AS^2}\Rightarrow AH=\frac{a\sqrt{6}}{3}\)
Vậy suy ra \(d\left(M,\left(SCD\right)\right)=\frac{a\sqrt{6}}{3}\)
.jpg)
E=AB∩CD,G=EN∩SB⇒GE=AB∩CD,G=EN∩SB⇒G là trọng tâm tam giác SAE.
d(M,(NCD))=GMGBd(B,(NCD))=12d(B,(NCD))=12.12d(A,(NCD))=14d(A,(NCD))=

1: BD vuông góc AC
BD vuông góc SA
=>BD vuông góc (SAC)
=>(SAC) vuông góc (SBD)



với AB = a, AD = a√2, ba cạnh SA, AB, AD đôi một vuông góc và SA = 2a. Gọi I là trung điểm SD. Tính cos(∠ISC).
Tóm tắt đề:
Bước 1: Đặt hệ trục tọa độ
\(I \left(\right. 0 , \frac{a \sqrt{2}}{2} , a \left.\right)\)
Bước 2: Tính vector IS và IC
Bước 3: Tính cos(∠ISC)
Ta cần tính góc giữa hai vector IS và IC.
\(cos \theta = \frac{\overset{⃗}{I S} \cdot \overset{⃗}{I C}}{\mid \overset{⃗}{I S} \mid \cdot \mid \overset{⃗}{I C} \mid}\)
$= 0 + \left(-a\sqrt{2}/2 \cdot a\sqrt{2}/2\right) + (-a^2)$
$= 0 + \left(-a^2 \cdot 2 / 4\right) - a^2$
$= -a^2/2 - a^2 = -3a^2/2$
Vậy:
\(cos \theta = \frac{- 3 a^{2} / 2}{a^{2} \sqrt{15} / 2} = - \frac{3}{\sqrt{15}} = - \frac{\sqrt{15}}{5}\)
Đáp số:
\(\boxed{cos \left(\right. \angle I S C \left.\right) = - \frac{\sqrt{15}}{5}}\)