Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi điểm được đặt là M
=>ΔAMC vuông tại A
=>AC<AM
=>Ko nghe rõ được bởi AM>550m
Gọi D là địa điểm đặt loa truyền thanh
Ta có: góc A=90°
=> AC là đường vuông góc
=> CD là đường xiên
Dó đó: AC<CD
Hay CD>550m( vì AC=550m )
Vậy tại C ko thể nghe rõ tiếng loa

Vì \(\widehat{A} \) là góc tù `=>` Cạnh `BC` là cạnh lớn nhất
`=> BC > AC`
Mà bán kính nghe rõ của loa là `500m`
`=>` Từ khoảng cách đó không thể nghe thấy được.

góc B>90 độ
=>góc BMA<90 độ
=>góc CMA>90 độ
=>CA>AM
=>AM<600
=>Ko thể nghe thấy đc

A B C M K I N H
Gọi H chân đường vuông góc kẻ từ M đến cạnh AB.
N là điểm nằm trên tia đối của IK sao cho IK=IN.
Ta thấy ngay: \(\Delta\)MIK=\(\Delta\)BIN (c.g.c) => MK=BN (2 cạnh tương ứng) (1)
Ta có: ^KCM + ^ACB = 900 ; ^HMB + ^ABC = ^KMC + ^ABC = 900 (Vì \(\Delta\)BHM vuông tại H)
Lại có: ^ABC=^ACB => ^KCM = ^KMC => \(\Delta\)MKC cân đỉnh K => MK=CK (2)
Từ (1) và (2) => CK=BN
Do \(\Delta\)MIK=\(\Delta\)BIN (cmt) => ^IKM=^INB => MK//BN (2 góc so le trg bằng nhau)
Mà MK vuông góc AB tại H => BN vuông góc AB hay ^ABN=900
Xét \(\Delta\)ACK và \(\Delta\)ABN: AC=AB; ^ACK=^ABN=900; CK=BN (cmt)
=> \(\Delta\)ACK=\(\Delta\)ABN (c.g.c) => AK=AN (2 cạnh tương ứng)
=> \(\Delta\)NAK cân đỉnh A. Mà I là trung điểm NK
=> AI là đường cao \(\Delta\)NAK. Hay AI vuông góc IK (đpcm).
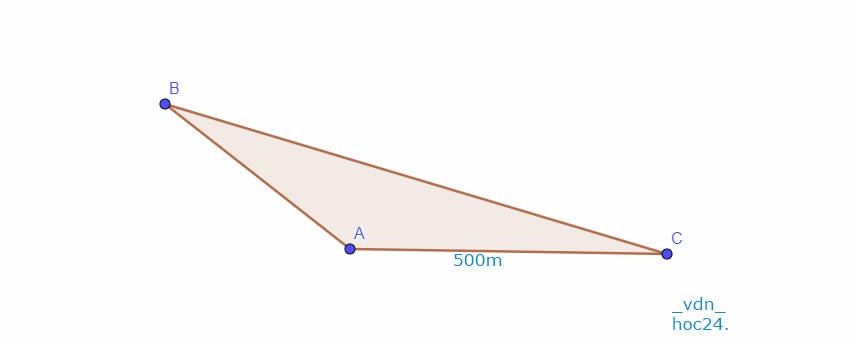
Tam giác \(A B C\) vuông tại \(A\) với \(A C = 500\) m. Vì khoảng cách ngắn nhất từ \(C\) đến \(A B\) chính là \(A C = 500\) m, bằng đúng bán kính truyền âm của loa, nên nếu loa đặt tại \(A\), \(C\) vẫn nghe được. Nhưng nếu loa đặt xa hơn trên đoạn \(A B\), khoảng cách từ loa đến \(C\) sẽ lớn hơn 500 m, khiến \(C\) không nghe được. Vậy \(C\) chỉ nghe được nếu loa đặt tại \(A\) hoặc rất gần \(A\).
Tam giác \(A B C\) vuông tại \(A\) với \(A C = 500\) m. Vì khoảng cách ngắn nhất từ \(C\) đến \(A B\) chính là \(A C = 500\) m, bằng đúng bán kính truyền âm của loa, nên nếu loa đặt tại \(A\), \(C\) vẫn nghe được. Nhưng nếu loa đặt xa hơn trên đoạn \(A B\), khoảng cách từ loa đến \(C\) sẽ lớn hơn 500 m, khiến \(C\) không nghe được. Vậy \(C\) chỉ nghe được nếu loa đặt tại \(A\) hoặc rất gần \(A\).