K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
S
subjects
CTVHS
24 tháng 8
bài 1:
\(A=-2xy+\frac32xy^2+\frac12xy^2+xy-3\)
\(=\left(\frac32+\frac12\right)xy^2+\left(-2xy+xy\right)-3\)
\(=2xy^2-xy-3\) (bậc 3)
\(B=-xy^2z+2x^2yz-xyz-3xy^2z-2x^2yz\)
\(=\left(2x^2yz-2x^2yz\right)+\left(-xy^2z-3xy^2z\right)-xyz\)
\(=-4xy^2z-xyz\) (bậc 4)
\(C=4x^2y^3+x^4-2x^2y^3+5x^4-2x^2y^3+3\)
\(=\left(4-2-2\right)x^2y^3+\left(1+5\right)x^4+3\)
\(=6x^4+3\) (bậc 4)
\(D=\frac34xy^2-2xy+3-\frac12xy^2-4xy-7\)
\(=\left(\frac34-\frac12\right)xy^2+\left(-2xy-4xy\right)+\left(3-7\right)\)
\(=\frac14xy^2-6xy-4\) (bậc 3)
\(E=-\frac34x^2y-5xy+\frac12x^2y+10xy-x^2y+xy\)
\(=\left(-\frac34+\frac12-1\right)x^2y+\left(-5+10+1\right)xy\)
\(=-\frac54x^2y+6xy\) (bậc 3)
\(F=3xy^2z-xy^2z-xyz+2xy^2z-3xyz-5xy^2z\)
\(=\left(3-1+2-5\right)xy^2z+\left(-1-3\right)xyz\)
\(=-xy^2z-4xyz\) (bậc 4)
bài 2; 1. thay x=y=-1 vào A ta được:
\(A=6\left(-1\right)\left(-1\right)^2+7\left(-1\right)\left(-1\right)^3+8\left(-1\right)^2\left(-1\right)^3=-7\)
2. \(B=x^6+2x^2y^3-x^2+xy-x^2y^3-x^6+x^5=x^2y^3+xy\)
thay x=-2; y=-1 vào B ta được:
\(4\cdot\left(-1\right)+2=-2\)
3. \(C=7xy^2-4xy+2xy^2-xy-9xy^2+5xy-\frac12x^2y^3=-\frac12x^2y^3\)
thay x = 15; y = -3 vào C ta được:
\(C=-\frac12\cdot15^2\cdot\left(-3\right)^3=3037,5\)
4. \(D=\frac23x^2y+3x^2y-x^2y-1=\frac83x^2y-1\)
thay x = -3; y = 1 vào D ta được:
\(\frac83\cdot\left(-3\right)^2\cdot1-1=23\)
bài 4:
1. \(A+B=\left(x+2y\right)+\left(x-2y\right)=2x\)
\(A-B=\left(x+2y\right)-\left(x-2y\right)=4y\)
2. \(B+A=\left(x^3+2xy^2-2\right)+\left(2x^2y-x^3-3xy^2+1\right)\)
\(=2x^2y+\left(2xy^2-xy^2\right)+\left(-2+1\right)\)
\(=2x^2y+xy^2-1\)
\(B-A=\left(x^3+2xy^2-2\right)-\left(2x^2y-x^3-xy^2+1\right)\)
\(=x^3+2xy^2-2-2x^2y+x^3+xy^2-1\)
\(=2x^3-2x^2y+3xy^2-3\)
3. \(A-B=\left(\frac12x^2y+xy^3-\frac52x^3y^2+x^3\right)-\left(\frac72x^3y^2-\frac12x^2y+xy^3\right)\)
\(=\frac12x^2y+\frac12x^2y+\left(xy^3-xy^3\right)+\left(-\frac52-\frac72\right)x^3y^2+x^3\)
\(=x^2y-6x^3y^2+x^3\)
\(B-A=-\left(A-B\right)=-\left(x^2y-6x^3y^2+x^3\right)=6x^3y^2-x^2y-x^3\)
27 tháng 8
Bài 6:
a: Xét tứ giác AMCK có
I là trung điểm chung của AC và MK
=>AMCK là hình bình hành
b: ΔABC vuông tại A
mà AM là đường trung tuyến
nên AM=MB=MC
Xét hình bình hành AMCK có MA=MC
nên AMCK là hình thoi
c: Ta có: AMCK là hình thoi
=>AK//CM và AK=CM
AK//CM
=>AK//MB
Ta có: AK=CM
CM=MB
Do đó; AK=MB
Xét tứ giác ABMK có
AK//MB
AK=MB
Do đó; ABMK là hình bình hành
d: Xét tứ giác ABEC có
M là trung điểm chung của AE và BC
=>ABEC là hình bình hành
Hình bình hành ABEC có AB=AC
nên ABEC là hình thoi
Bài 5:
a: Xét ΔAHD vuông tại H và ΔCKB vuông tại K có
AD=CB
\(\hat{ADH}=\hat{CBK}\) (hai góc so le trong, AD//BC)
Do đó: ΔAHD=ΔCKB
b: ΔAHD=ΔCKB
=>HD=KB; AH=CK
ta có: AH⊥BD
CK⊥BD
Do đó:AH//CK
Xét tứ giác AHCK có
AH//CK
AH=CK
Do đó: AHCK là hình bình hành
c: Ta có: AH//CK
=>AM//CN
ta có: AB//CD
=>AN//CM
Xét tứ giác ANCM có
AN//CM
AM//CN
Do đó: ANCM là hình bình hành
d: Ta có; ANCM là hình bình hành
=>AC cắt NM tại trung điểm của mỗi đường(1)
Ta có:ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường(2)
Từ (1),(2) suy ra AC,MN,BD đồng quy
Bài 2:
a: Ta có: \(AE=EB=\frac{AB}{2}\)
\(DF=FC=\frac{DC}{2}\)
mà AB=CD
nên AE=EB=DF=FC
Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
b: Xét tứ giác BEDF có
BE//DF
BE=DF
Do đó: BEDF là hình bình hành
=>DE//BF
=>FN//EM
Ta có: AECF là hình bình hành
=>AF//CE
=>FM//EN
Xét tứ giác MENF có
ME//NF
MF//NE
Do đó: MENF là hình bình hành
c: Ta có: MENF là hình bình hành
=>MN cắt EF tại trung điểm của mỗi đường(1)
Ta có: AECF là hình bình hành
=>AC cắt EF tại trung điểm của mỗi đường(2)
Từ (1),(2) suy ra AC,EF,MN đồng quy
23 tháng 8
a: ta có: EI⊥BF
AC⊥BF
Do đó: EI//AC
=>\(\hat{IEB}=\hat{ACB}\) (hai góc đồng vị)
mà \(\hat{ABC}=\hat{ACB}\) (ΔABC cân tại A)
nên \(\hat{KBE}=\hat{IEB}\)
Xét ΔKBE vuông tại K và ΔIEB vuông tại I có
BE chung
\(\hat{KBE}=\hat{IEB}\)
Do đó: ΔKBE=ΔIEB
=>EK=BI
b: Điểm D ở đâu vậy bạn?
19 tháng 8
\(\frac{9x+5}{6\cdot\left(x+3\right)^2}-\frac{5x-7}{6\left(x+3\right)^2}\)
\(=\frac{9x+5-5x+7}{6\left(x+3\right)^2}\)
\(=\frac{4x+12}{6\left(x+3\right)^2}=\frac{4\left(x+3\right)}{6\left(x+3\right)^2}=\frac{2}{3\left(x+3\right)}\)
11 tháng 8
Bài 4:
AB//CD
=>\(\hat{BAK}=\hat{AKD}\) (hai góc so le trong)
mà \(\hat{BAK}=\hat{DAK}\) (AK là phân giác của góc BAD)
nên \(\hat{DAK}=\hat{DKA}\)
=>DA=DK
Ta có: DK+KC=DC
DA+BC=DC
mà DK=DA
nên CK=CB
=>ΔCKB cân tại C
=>\(\hat{CKB}=\hat{CBK}\)
mà \(\hat{CKB}=\hat{ABK}\) (hai góc so le trong, AB//CD)
nên \(\hat{ABK}=\hat{CBK}\)
=>BK là phân giác của góc ABC
Bài 2:
a: Xét ΔDAB có
K,E lần lượt là trung điểm của DA,DB
=>KE là đường trung bình của ΔDAB
=>KE//AB và \(KE=\frac{AB}{2}\)
Xét ΔCAB có
F,G lần lượt là trung điểm của CA,CB
Do đó: FG là đường trung bình của ΔCAB
=>FG//AB và \(FG=\frac{AB}{2}\)
Xét hình thang ABCD có
K,G lần lượt là trung điểm của AD,BC
=>KG là đường trung bình của hình thang ABCD
=>KG//AB//CD và \(KG=\frac12\left(AB+CD\right)\)
Ta có: FG//AB
KG//AB
FG,KG có điểm chung là G
Do đó: F,G,K thẳng hàng(1)
ta có: KE//AB
KG//AB
KE,KG có điểm chung là K
Do đó: K,E,G thẳng hàng(2)
Từ (1),(2) suy ra K,E,F,G thẳng hàng
b: Ta có: KE+EF+FG=KG
=>\(EF+\frac12AB+\frac12AB=\frac12\left(CD+AB\right)\)
=>\(EF=\frac12\left(CD+AB-2AB\right)=\frac12\left(CD-AB\right)\)
16 tháng 8
a: Xét ΔBDE vuông tại E và ΔBCD vuông tại D có
\(\hat{DBE}\) chung
Do đó: ΔBDE~ΔBCD
b: Xét ΔBFD vuông tại F và ΔBDA vuông tại D có
\(\hat{FBD}\) chung
Do đó: ΔBFD~ΔBDA
=>\(\frac{BF}{BD}=\frac{BD}{BA}\)
=>\(BD^2=BF\cdot BA\)
c: ΔBDE~ΔBCD
=>\(\frac{BD}{BC}=\frac{BE}{BD}\)
=>\(BD^2=BE\cdot BC\)
=>\(BE\cdot BC=BF\cdot BA\)
=>\(\frac{BE}{BA}=\frac{BF}{BC}\)
Xét ΔBEF và ΔBAC có
\(\frac{BE}{BA}=\frac{BF}{BC}\)
góc EBF chung
Do đó: ΔBEF~ΔBAC
=>\(\hat{BFE}=\hat{BCA}\)
16 tháng 8
Gọi I là trung điểm của DE
=>I là tâm đường tròn đường kính DE
ĐƯờng trung trực của BC cắt BC,AC,AB lần lượt tại M,D,E
=>MB=MC; EB=EC; DB=DC
MB=MC nên M la trung điểm của BC
ΔABC vuông tại A
mà AM là đường trung tuyến
nên MA=MB
=>ΔMAB cân tại M
=>\(\hat{MAB}=\hat{MBA}\)
ΔAED vuông tại A
mà AI là đường trung tuyến
nên IA=IE
=>ΔIAE cân tại I
=>\(\hat{IAE}=\hat{IEA}\)
mà \(\hat{IEA}=\hat{MEB}\) (hai góc đối đỉnh)
nên \(\hat{IAE}=\hat{MEB}\)
Ta có: DM là đường trung trực của BC
=>DM⊥BC tại M
Xét tứ giác AEMC có \(\hat{CAE}+\hat{CME}+\hat{ACM}+\hat{AEM}=360^0\)
=>\(\hat{ACM}+\hat{AEM}=360^0-90^0-90^0=180^0\)
mà \(\hat{AEM}+\hat{BEM}=180^0\) (hai góc kề bù)
nên \(\hat{BEM}=\hat{ACB}\)
\(\hat{MAI}=\hat{MAE}+\hat{IAE}=\hat{MAB}+\hat{MEB}\)
\(=\hat{MBA}+\hat{MCA}=90^0\)
=>AM⊥IA tại A
ΔAED vuông tại A
mà AI là đường trung tuyến
nên IA=IE=ID
=>A nằm trên (I)
Xét (I) có
IA là bán kính
AM⊥ AI tại A
Do đó: AM là tiếp tuyến tại A của (I)
=>AM là tiếp tuyến của đường tròn đường kính DE
18 tháng 8
Xét tứ giác APMQ có \(\hat{APM}=\hat{AQM}=\hat{PAQ}=90^0\)
nên APMQ là hình chữ nhật
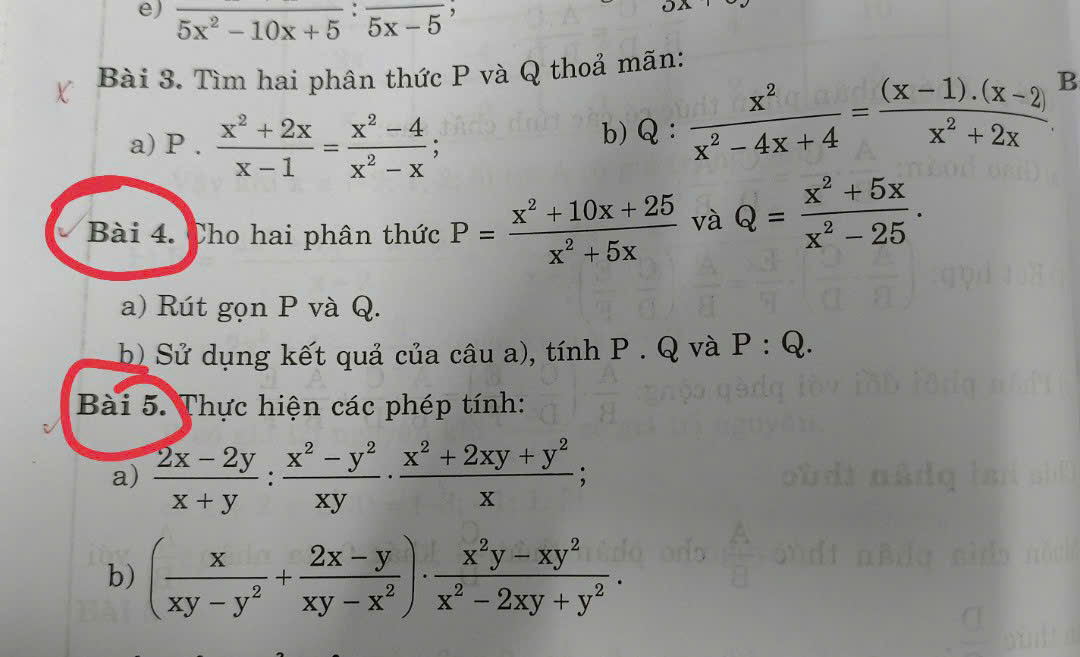
Bài 4:
a: \(P=\dfrac{x^2+10x+25}{x^2+5x}=\dfrac{\left(x+5\right)^2}{x\left(x+5\right)}=\dfrac{x+5}{x}\)
\(Q=\dfrac{x^2+5x}{x^2-25}=\dfrac{x\left(x+5\right)}{\left(x+5\right)\left(x-5\right)}=\dfrac{x}{x-5}\)
b: \(P\cdot Q=\dfrac{x+5}{x}\cdot\dfrac{x}{x-5}=\dfrac{x+5}{x-5}\)
\(P:Q=\dfrac{x+5}{x}:\dfrac{x}{x-5}=\dfrac{\left(x+5\right)\left(x-5\right)}{x^2}=\dfrac{x^2-25}{x^2}\)
Bài 5:
a: \(\dfrac{2x-2y}{x+y}:\dfrac{x^2-y^2}{xy}\cdot\dfrac{x^2+2xy+y^2}{x}\)
\(=\dfrac{2\left(x-y\right)}{x+y}\cdot\dfrac{xy}{\left(x-y\right)\left(x+y\right)}\cdot\dfrac{\left(x+y\right)^2}{x}\)
\(=\dfrac{2xy\left(x+y\right)^2}{\left(x+y\right)^2\cdot x}=2y\)
b: \(\left(\dfrac{x}{xy-y^2}+\dfrac{2x-y}{xy-x^2}\right)\cdot\dfrac{x^2y-xy^2}{x^2-2xy+y^2}\)
\(=\left(\dfrac{x}{y\left(x-y\right)}-\dfrac{2x-y}{x\left(x-y\right)}\right)\cdot\dfrac{xy\left(x-y\right)}{\left(x-y\right)^2}\)
\(=\dfrac{x^2-y\left(2x-y\right)}{xy\left(x-y\right)}\cdot\dfrac{xy}{x-y}\)
\(=\dfrac{x^2-2xy+y^2}{\left(x-y\right)^2}=1\)
Bài 4:
a: \(P = \frac{x^{2} + 10 x + 25}{x^{2} + 5 x} = \frac{\left(\left(\right. x + 5 \left.\right)\right)^{2}}{x \left(\right. x + 5 \left.\right)} = \frac{x + 5}{x}\)
\(Q = \frac{x^{2} + 5 x}{x^{2} - 25} = \frac{x \left(\right. x + 5 \left.\right)}{\left(\right. x + 5 \left.\right) \left(\right. x - 5 \left.\right)} = \frac{x}{x - 5}\)
b: \(P \cdot Q = \frac{x + 5}{x} \cdot \frac{x}{x - 5} = \frac{x + 5}{x - 5}\)
\(P : Q = \frac{x + 5}{x} : \frac{x}{x - 5} = \frac{\left(\right. x + 5 \left.\right) \left(\right. x - 5 \left.\right)}{x^{2}} = \frac{x^{2} - 25}{x^{2}}\)
Bài 5:
a: \(\frac{2 x - 2 y}{x + y} : \frac{x^{2} - y^{2}}{x y} \cdot \frac{x^{2} + 2 x y + y^{2}}{x}\)
\(= \frac{2 \left(\right. x - y \left.\right)}{x + y} \cdot \frac{x y}{\left(\right. x - y \left.\right) \left(\right. x + y \left.\right)} \cdot \frac{\left(\left(\right. x + y \left.\right)\right)^{2}}{x}\)
\(= \frac{2 x y \left(\left(\right. x + y \left.\right)\right)^{2}}{\left(\left(\right. x + y \left.\right)\right)^{2} \cdot x} = 2 y\)
b: \(\left(\right. \frac{x}{x y - y^{2}} + \frac{2 x - y}{x y - x^{2}} \left.\right) \cdot \frac{x^{2} y - x y^{2}}{x^{2} - 2 x y + y^{2}}\)
\(= \left(\right. \frac{x}{y \left(\right. x - y \left.\right)} - \frac{2 x - y}{x \left(\right. x - y \left.\right)} \left.\right) \cdot \frac{x y \left(\right. x - y \left.\right)}{\left(\left(\right. x - y \left.\right)\right)^{2}}\)
\(= \frac{x^{2} - y \left(\right. 2 x - y \left.\right)}{x y \left(\right. x - y \left.\right)} \cdot \frac{x y}{x - y}\)
\(= \frac{x^{2} - 2 x y + y^{2}}{\left(\left(\right. x - y \left.\right)\right)^{2}} = 1\)