Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tam giác \(PBC\)và tam giác \(PAB\)có:
\(\frac{PB}{PA}=\frac{BC}{AB}=\frac{PC}{PB}=\sqrt{2}\)
suy ra \(\Delta PBC~\Delta PAB\left(c.c.c\right)\)
suy ra \(\widehat{PBC}=\widehat{PAB}\).
\(\widehat{APB}=180^o-\widehat{PAB}-\widehat{PBA}=180^o-\widehat{PBC}-\widehat{PBA}=180^o-\widehat{ABC}\)
\(=180^o-45^o-135^o\)

Đáp án C
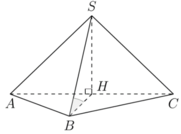
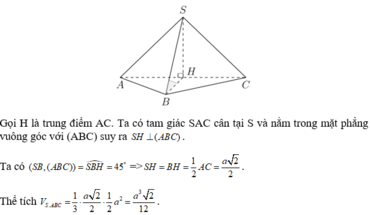
Gọi H là trung điểm AC. Ta có tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với (ABC)
suy ra S H ⊥ A B C
Ta có
S B , A B C = S B H ^ = 45 o ⇒ S H = B H = 1 2 A C = a 2 2 V S . A B C = 1 3 . a 2 2 . 1 2 a 2 = a 3 2 12

Chọn A
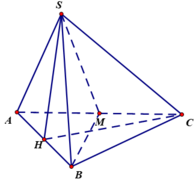
Gọi H là trung điểm của AB. Theo bài ra:
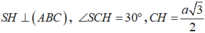
Xét tam giác SCH ta có:


a) Tính \(V_{S.ABM}\)
Tam giác ABC cân tại A , SBC cân tại S \(\Rightarrow AM\perp BC;SM\perp BC\) tại M
Vì mp(SBC) vuông góc với mặt đáy suy ra SM vuông góc với mặt đáy
Góc giữa SB và mặt đáy là góc SBM=300
\(\Rightarrow SM=BMtan.\widehat{SBM}=\frac{a}{2}.tan30^0=\frac{a}{2\sqrt{3}}\)
\(\Rightarrow V_{S.ABM}=\frac{1}{3}.SM.S_{ABM}=\frac{1}{3}.\frac{a}{2\sqrt{3}}.\frac{1}{2}.\frac{a}{2}.\frac{a\sqrt{3}}{2}=\frac{a^3}{48}\)
b) Tính k/c SB và AM
Kẻ MH vuông góc với SB tại H
Dễ dàng chứng minh MH là đoạn vuông góc chung giữa SB và AM
Vậy khảong cách giữa SB và AM bằng đoạn MH và bằng \(\frac{BM}{cos.\widehat{HBM}}=\frac{\frac{a}{2}}{cos30^0}=\frac{a}{\sqrt{3}}\)
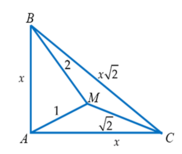




Để tính góc ∠APB\angle APB, ta cần sử dụng một số công thức và định lý trong hình học. Đầu tiên, vì tam giác ABC vuông cân tại A nên các cạnh AB và AC đều bằng nhau.
Giả sử AB = AC = x.
Vì P nằm trong tam giác ABC và ta biết các đoạn PA, PB, PC, ta có thể sử dụng định lý cosine trong các tam giác PAB và PAC để tính các góc cần thiết.
Gọi các đoạn thẳng:
Để đơn giản hóa, chúng ta cần thực hiện phép biến đổi logarit trên PB:
\[ PB = 6^{84} = (62){42} = 36^{42} \]
Việc này cho thấy giá trị của PB rất lớn và có thể khó tính toán trực tiếp. Tuy nhiên, điều này không ảnh hưởng đến việc tính góc vì ta chủ yếu sử dụng định lý cosine để so sánh và tính toán góc.
Từ định lý cosine trong tam giác PAB:
cos(∠APB)=PA2+PB2−AB22⋅PA⋅PB\cos(\angle APB) = \frac{PA^2 + PB^2 - AB^2}{2 \cdot PA \cdot PB}Tương tự trong tam giác PAC:
cos(∠APC)=PA2+PC2−AC22⋅PA⋅PC\cos(\angle APC) = \frac{PA^2 + PC^2 - AC^2}{2 \cdot PA \cdot PC}Vì PA, PB, và PC đã biết, ta có thể tính hai góc này. Tuy nhiên, để giải bài toán chính xác, ta cần các giá trị của AB và AC, mà đã được giả định là bằng nhau.
Trong trường hợp cụ thể này với giá trị PB lớn, việc tính toán trực tiếp các giá trị có thể dẫn đến các giá trị gần đúng.
Tuy nhiên, bài toán này khá phức tạp và có thể yêu cầu sự tham gia của các công cụ toán học cao cấp hơn hoặc việc sử dụng phần mềm để giải quyết chính xác hơn.
Tôi hy vọng hướng dẫn này giúp bạn hiểu cách tiếp cận bài toán. Nếu có thắc mắc cụ thể hoặc cần thêm hướng dẫn, bạn hãy cho tôi biết nhé!