QT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
SC
4 tháng 4 2021
b, xét pt hoành độ giao điểm:
-x²=4x+m
=> x²+4x+m=0
a=1. b= 4. c=m
Để pt có 2 No pb=> ∆>0
<=>4²-4×1×m>0
<=>16-4m>0
<=> -4m>-16
<=> m<16÷4=4
Vậy m=4 pt có 2No pb
DT
0
23 tháng 12 2023
Câu 5:
a: Khi m=3 thì \(f\left(x\right)=\left(2\cdot3+1\right)x-3=7x-3\)
\(f\left(-3\right)=7\cdot\left(-3\right)-3=-21-3=-24\)
\(f\left(0\right)=7\cdot0-3=-3\)
b: Thay x=2 và y=3 vào f(x)=(2m+1)x-3, ta được:
\(2\left(2m+1\right)-3=3\)
=>2(2m+1)=6
=>2m+1=3
=>2m=2
=>m=1
c: Thay m=1 vào hàm số, ta được:
\(y=\left(2\cdot1+1\right)x-3=3x-3\)
*Vẽ đồ thị
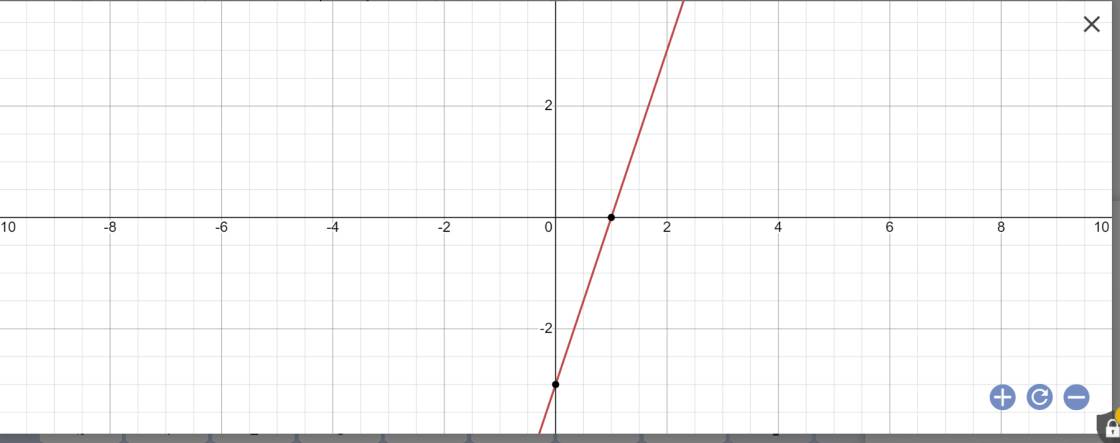
d: Để hàm số y=(2m+1)x-3 là hàm số bậc nhất thì \(2m+1\ne0\)
=>\(2m\ne-1\)
=>\(m\ne-\dfrac{1}{2}\)
e: Để đồ thị hàm số y=(2m+1)x-3 song song với đường thẳng y=5x+1 thì \(\left\{{}\begin{matrix}2m+1=5\\-3\ne1\end{matrix}\right.\)
=>2m+1=5
=>2m=4
=>m=2
19 tháng 8 2016
\(\left|2m^2-7\right|-27=-2\)
\(\Leftrightarrow\left|2m^2-7\right|=25\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}2m^2-7=25\\7-2m^2=25\left(loai\right)\end{array}\right.\)
\(\Leftrightarrow m=\pm4\)
19 tháng 8 2016
ĐTHS trên đi qua M(1;-2) tức là \(-2=\left|2m^2-7\right|-27\Leftrightarrow\left|2m^2-7\right|=25\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}2m^2-7=25\\2m^2-7=-25\end{array}\right.\) \(\Leftrightarrow\left[\begin{array}{nghiempt}2m^2=32\left(\text{nhận}\right)\\2m^2=-18\left(\text{loại}\right)\end{array}\right.\)\(\Leftrightarrow m^2=16\Leftrightarrow m=\pm4\)
26 tháng 6 2016
\(\left|2m^2-7\right|-27=-2\)
\(\Rightarrow\left|2m^2-7\right|=25\)
\(\Rightarrow\left[\begin{array}{nghiempt}2m^2-7=25\\7-2m^2=25\left(loại\right)\end{array}\right.\)
\(\Rightarrow m=\pm4\)
HQ
Hà Quang Minh
Giáo viên
11 tháng 9 2023
Xét điểm \(M\left( { - 1; - 4} \right)\) ta có:
\(f\left( { - 1} \right) = 4.\left( { - 1} \right) = - 4\). Do đó, điểm \(M\left( { - 1; - 4} \right)\) thuộc vào đồ thị hàm số \(y = 4x\).
Xét điểm \(N\left( {1; - 4} \right)\) ta có:
\(f\left( 1 \right) = 4.1 = 4 \ne - 4\). Do đó, điểm \(N\left( {1; - 4} \right)\) không thuộc vào đồ thị hàm số \(y = 4x\).
Xét điểm \(P\left( {\dfrac{1}{4};1} \right)\) ta có:
\(f\left( {\dfrac{1}{4}} \right) = 4.\dfrac{1}{4} = 1\). Do đó, điểm \(P\left( {\dfrac{1}{4};1} \right)\) không thuộc vào đồ thị hàm số \(y = 4x\).
HQ
Hà Quang Minh
Giáo viên
12 tháng 9 2023
Đáp án đúng là D
+ Xét điểm \(\left( {1;1} \right)\) ta có: \(y = 2 - 4.1 = - 2 \ne 1\). Do đó, điểm \(\left( {1;1} \right)\)không thuộc đồ thị hàm số.
+ Xét điểm \(\left( {2;0} \right)\) ta có: \(y = 2 - 4.2 = - 6 \ne 2\). Do đó, điểm \(\left( {2;0} \right)\)không thuộc đồ thị hàm số.
+ Xét điểm \(\left( {1; - 1} \right)\) ta có: \(y = 2 - 4.1 = - 2 \ne - 1\). Do đó, điểm \(\left( {1; - 1} \right)\)không thuộc đồ thị hàm số.
+ Xét điểm \(\left( {1; - 2} \right)\) ta có: \(y = 2 - 4.1 = - 2\). Do đó, điểm \(\left( {1; - 2} \right)\) thuộc đồ thị hàm số.
AH
Akai Haruma
Giáo viên
27 tháng 11 2023
Lời giải:
a. Vì đths đi qua $A(-2;3)$ nên:
$y_A=(2m+5)x_A-1$
$\Rightarrow 3=(2m+5)(-2)-1\Rightarrow m=\frac{-7}{2}$
b. ĐTHS sau khi tìm được $m$ có pt: $y=-2x-1$. Bạn có thể tự vẽ
c. ĐTHS cắt trục hoành tại điểm có hoành độ -3, tức là đi qua điểm $(-3,0)$
$\Rightarrow 0=(2m+5)(-3)-1$
$\Rightarrow m=\frac{-8}{3}$
19 tháng 1 2024
a: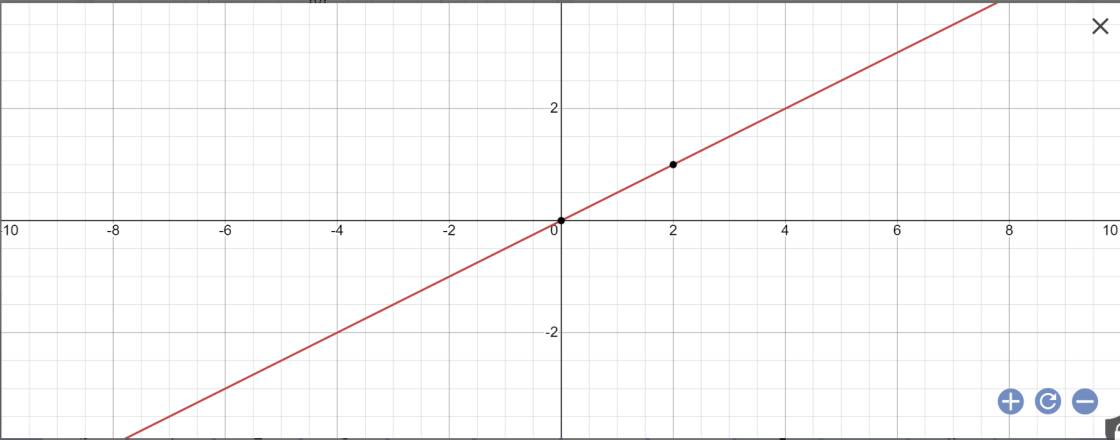 
b: \(f\left(2\right)=\dfrac{1}{2}\cdot2=1\)
\(f\left(1\right)=\dfrac{1}{2}\cdot1=\dfrac{1}{2}\)
\(f\left(-2\right)=\dfrac{1}{2}\cdot\left(-2\right)=-1\)
\(f\left(-1\right)=\dfrac{1}{2}\cdot\left(-1\right)=-\dfrac{1}{2}\)
\(f\left(0\right)=\dfrac{1}{2}\cdot0=0\)
c: f(x)=2
=>\(\dfrac{1}{2}x=2\)
=>x=2*2=4
f(x)=1
=>\(\dfrac{1}{2}x=1\)
=>\(x=1:\dfrac{1}{2}=2\)
f(x)=-1
=>\(\dfrac{1}{2}x=-1\)
=>\(x=-1\cdot2=-2\)
d: \(f\left(-1\right)=\dfrac{1}{2}\cdot\left(-1\right)=-\dfrac{1}{2}\ne\dfrac{1}{2}=y_A\)
=>A(-1;1/2) không thuộc đồ thị hàm số y=1/2x
\(f\left(-1\right)=\dfrac{1}{2}\cdot\left(-1\right)=-\dfrac{1}{2}=y_B\)
=>\(B\left(-1;-\dfrac{1}{2}\right)\) thuộc đồ thị hàm số y=1/2x
16 tháng 12 2023
a: Để hàm số y=(2m-1)x+m-1 nghịch biến trên R thì 2m-1<0
=>2m<1
=>\(m< \dfrac{1}{2}\)
b: Thay x=-1 và y=0 vào y=(2m-1)x+m-1, ta được:
-(2m-1)+m-1=0
=>-2m+1+m-1=0
=>-m=0
=>m=0
c: Thay x=1 và y=4 vào y=(2m-1)x+m-1, ta được:
2m-1+m-1=4
=>3m-2=4
=>3m=6
=>m=2
Khi m=2 thì \(y=\left(2\cdot2-1\right)x+2-1=3x+1\)
vẽ đồ thị:
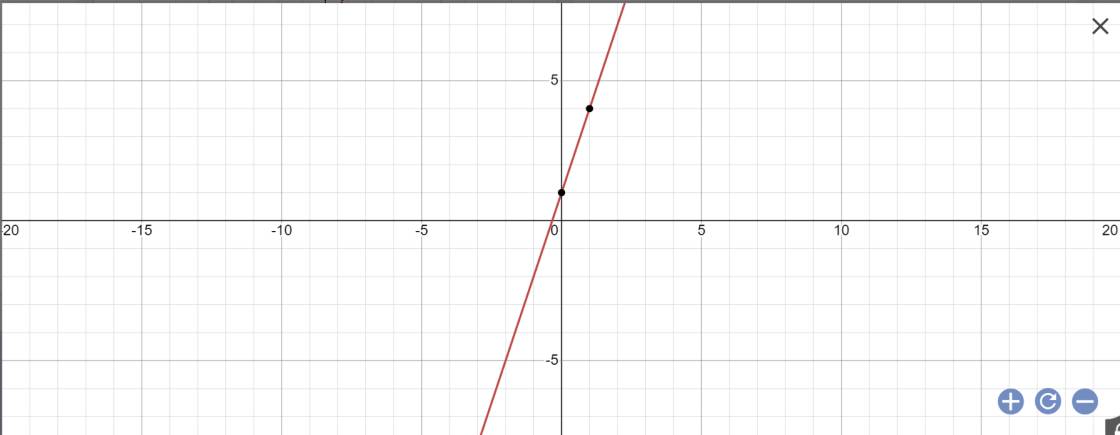
y=3x+1
=>3x-y+1=0
Khoảng cách từ O(0;0) đến đường thẳng 3x-y+1=0 là:
\(d\left(O;3x-y+1=0\right)=\dfrac{\left|0\cdot3+0\cdot\left(-1\right)+1\right|}{\sqrt{3^2+\left(-1\right)^2}}=\dfrac{1}{\sqrt{10}}\)
Thay x=-7 và y=1 vào y=-4x-27, ta được:
\(\left(-4\right)\cdot\left(-7\right)-27=1\)
=>28-27=1
=>1=1(đúng)
=>A(-7;1) thuộc đồ thị hàm số y=-4x-27