Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
A B C H F D E K L
+) Chứng minh tứ giác BFLK nội tiếp:
Ta thấy FAH và LAH là hai tam giác vuông có chung cạnh huyền AH nên AFHL là tứ giác nội tiếp. Vậy thì \(\widehat{ALF}=\widehat{AHF}\) (Hai góc nội tiếp cùng chắn cung AF)
Lại có \(\widehat{AHF}=\widehat{FBK}\) (Cùng phụ với góc \(\widehat{FAH}\) )
Vậy nên \(\widehat{ALF}=\widehat{FBK}\), suy ra tứ giác BFLK nội tiếp (Góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện)
+) Chứng minh tứ giác CELK nội tiếp:
Hoàn toàn tương tự : Tứ giác AELH nội tiếp nên \(\widehat{ALE}=\widehat{AHE}\) , mà \(\widehat{AHE}=\widehat{ACD}\Rightarrow\widehat{ALE}=\widehat{ACD}\)
Suy ra tứ giác CELK nội tiếp.

a, Ta co 2 bo de quen thuoc sau : FC la phan giac ^EFD, FB la phan giac PFD
ma QR//EP nen
\(\widehat{PFB}=\widehat{FQD}=\widehat{QFD}\Rightarrow\Delta DFQ\) can tai D => DF=DQ (1)
mat khac theo tinh chat tia phan giac ngoai ^PFD co \(\frac{FD}{FP}=\frac{CD}{CP}\)
ma \(\frac{CD}{CP}=\frac{DT}{PF}\) (DT//PF)
suy ra \(\frac{DF}{PF}=\frac{DT}{PF}\Rightarrow DT=DF\) (2)
Tu(1)va (2) suy ra DT=DQ hay D la trung diem QT
b, Goi S la trung diem BC ta chung minh PQSR noi tiep
Co \(\Delta PSE~\Delta ESD\left(G-G\right)\Rightarrow\frac{PS}{ES}=\frac{ES}{SD}\Leftrightarrow ES^2=PS.DS\)
lai co ES=SB=SC do S la trung diem canh huyen BC cua tam giac vuong BEC
suy ra \(BS^2=PS.SD=DS\left(PD+DS\right)=SD^2+PD.DS\)
=> \(PD.DS=BS^2-SD^2=\left(BS-DS\right)\left(BS+DS\right)=BD.DC\) (3)
Mat khac ^DQB=^PFB(cmt)
^PFB=^RCD( BFEC nt)
suy ra ^DQB=^RCD=> BQCR noi tiep
=> \(BD.DC=DQ.DR\) (4)
Tu (3),(4) suy ra DP.DS=DQ.DR => PQDR noi tiep
=> (PQR) di qua S la trung diem BC co dinh
c,lay H' doi xung voi H qua BC, ta co H' thuoc (O) .
ta lai co bo de sau : \(BD.DC=DH.DA\) (quen thuoc)
suy ra \(DP.DS=DH.DA\left(=DB.DC\right)\)
<=> \(\frac{DH}{DP}=\frac{DS}{DA}\)
ma ^HDP=^SDA=90
suy ra \(\Delta DHP~\Delta DSA\left(c-g-c\right)\Rightarrow\widehat{DHP}=\widehat{DSA}\)
va \(\widehat{DSA}=\widehat{AHK}\left(phu\widehat{DAS}\right)\)
=>\(\widehat{DHP}=\widehat{AHK}\) => P,H,K thang hang
lai co \(\widehat{AFH}=\widehat{AKH}=\widehat{AEH}=90\)
=> A,F,H,K,E cung thuoc 1 duong tron =. FHKE noi tiep
=>\(PF.PE=PH.PK\) (5)
ma BFEC noi tiep => \(PF.PE=PB.PC\) (6)
(5)+(6)Suy ra \(PH.PK=PB.PC\) => BHKC noi tiep
Vi H' ,I doi xung voi H,K qua BC ma BHKC noi tiep => BH'IC noi tiep
do vay \(I\in\left(BH'C\right)=\left(ABH'C\right)=\left(O\right)\)
e,Goi tam (CJL) la U, (U) cat (O) tai V, BC giao OG tai X
=> \(\widehat{VBG}=\widehat{VJG}\left(=\widehat{VCB}\right)\) =>BJVG noi tiep
=> B,J,X,V,G cung thuoc 1 duong tron => ^BVG=^BXG=90
lai co ^XVG +^XBG=180 hay ^XVG+^BAC=180
va ^BVC+^BAC=180
suy ra ^XVG=^BVC
hay 90 +^XVB=^XVB+^XVC
=> ^XVC=90
=> V thuoc duong tron dk XC
mat khac V cung thuoc (O)
suy ra V co dinh ,C co dinh
suy ra tam U di chuyen tren trung truc VC co dinh (dpcm)

A B C E F L M N K
Theo định lí Pytago 4 điểm ta có:
\(KB^2-KL^2=MB^2-ML^2\) vì \(MK\perp BL\)
\(KC^2-KL^2=NC^2-NL^2\) vì \(NK\perp CL\)
Suy ra \(KB^2-KC^2=MB^2-NC^2+NL^2-ML^2\)
\(=\frac{1}{4}\left(BF^2-CE^2+CF^2-BE^2\right)=\frac{1}{4}\left(BC^2-BC^2\right)=0\)
Vậy \(KB=KC.\)

\({}\)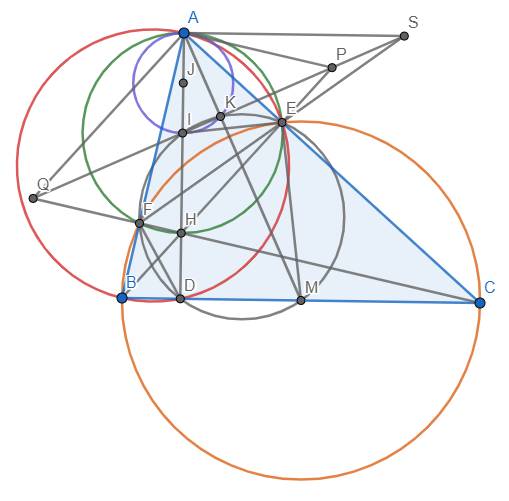
a) Vì \(\widehat{BEC}=\widehat{BFC}=90^o\) nên tứ giác BEFC nội tiếp đường tròn đường kính BC. Tương tự như thế, tứ giác AEDB nội tiếp đường tròn đường kính AB. Cũng có \(\widehat{AEH}=\widehat{AFH}=90^o\) nên tứ giác AEHF nội tiếp đường tròn đường kính AH.
Ta có \(\widehat{IEM}=\widehat{IEB}+\widehat{BEM}\)
\(=\left(90^o-\widehat{IEA}\right)+\widehat{EBC}\)
\(=90^o-\widehat{EAD}+\widehat{EBD}=90^o\) (do \(\widehat{EBD}=\widehat{EAD}\))
Vậy \(IE\perp ME\)
b) Dễ thấy các điểm I, D, E, F, M, K cùng thuộc đường tròn đường kính IM. Gọi J là trung điểm AI thì I chính là tâm của đường tròn (AIK) nên (J) tiếp xúc với (I) tại A. Dẫn đến A nằm trên trục đẳng phương của (I) và (J)
Mặt khác, ta có \(SK.SI=SE.SF\) nên \(P_{S/\left(I\right)}=P_{S/\left(J\right)}\) hay S nằm trên trục đẳng phương của (I) và (J). Suy ra AS là trục đẳng phương của (I) và (J). \(\Rightarrow\)\(AS\perp IJ\) hay AS//BC (đpcm).
c) Ta thấy tứ giác AKEP nội tiếp đường tròn AP
\(\Rightarrow\widehat{APB}=\widehat{MKE}=\widehat{MDE}=\widehat{BAC}\)
\(\Rightarrow\Delta BAE~\Delta BPA\left(g.g\right)\Rightarrow\widehat{BAP}=\widehat{BEA}=90^o\)
\(\Rightarrow\) AP//QH \(\left(\perp AB\right)\)
\(\Rightarrow\widehat{IAP}=\widehat{IHQ}\) (2 góc so le trong)
Từ đó dễ dàng chứng minh \(\Delta IAP=\Delta IHQ\left(g.c.g\right)\) \(\Rightarrow IP=IQ\) hay I là trung điểm PQ (đpcm)


Ta có:ˆGHF+ˆHGF=90°GHF^+HGF^=90° (do DGHF vuông tại F) và ˆCHM+ˆCHK=90°CHM^+CHK^=90°
Mà ˆGHF=ˆCHKGHF^=CHK^ (đối đỉnh) nên ˆHGF=ˆCHMHGF^=CHM^ hay ˆHGA=ˆCHMHGA^=CHM^
Ta có: ˆBAD+ˆABD=90°BAD^+ABD^=90° (do DABD vuông tại D);
ˆBCF+ˆCBF=90°BCF^+CBF^=90° (do DBCF vuông tại F)
Do đó ˆBAD=ˆBCFBAD^=BCF^ hay ˆGAH=ˆMCHGAH^=MCH^
Xét DGAH và DCHM có: ˆHGA=ˆCHMHGA^=CHM^và ˆGAH=ˆMCHGAH^=MCH^
Do đó ΔGAH ∽ΔHCM(g.g)ΔGAH ∽ΔHCMg.g
Suy ra GHHM=AHCMGHHM=AHCM (tỉ số đồng dạng) (1)
Tương tự, ta có: ΔAHK ∽ΔBMH(g.g)ΔAHK ∽ΔBMHg.g
Suy ra AHBM=HKMHAHBM=HKMH (tỉ số đồng dạng) (2)
Mặt khác: M là trung điểm của BC nên CM = BM (3)
Từ (1), (2) và (3) ta có:GHHM=HKMHGHHM=HKMH , suy ra GH = HK.