Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

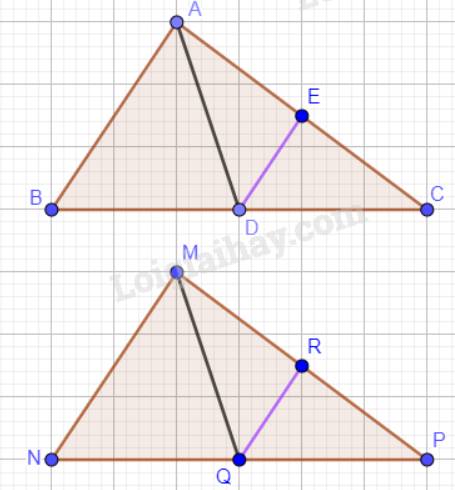
a) Xét hai tam giác ABD và tam giác MNQ:
AB = MQ (do \(\Delta ABC = \Delta MNP\)).
\(\widehat {ABD} = \widehat {MNQ}\) (\(\widehat {ABD} = \widehat {MNQ}\)).
BD = NQ (\(\dfrac{1}{2}BC = \dfrac{1}{2}NP\))
BC = NP (do \(\Delta ABC = \Delta MNP\)).
Vậy \(\Delta ABD = \Delta MNQ\)(c.g.c) nên AD = MQ ( 2 cạnh tương ứng)
b) Vì \(\Delta ABC = \Delta MNP\) nên BC = NP ( 2 cạnh tương ứng) . Do đó, \(\dfrac{1}{2}BC = \dfrac{1}{2}NP\) hay DC = QP
Vì \(\Delta ABC = \Delta MNP\) nên AC = MP ( 2 cạnh tương ứng) . Do đó, \(\dfrac{1}{2}AC = \dfrac{1}{2}MP\) hay EC = RP
Xét hai tam giác DEC và tam giác QRP:
DC = QP
\(\widehat {ECD} = \widehat {RPQ}\)(\(\Delta ABC = \Delta MNP\))
EC = RP
Vậy \(\Delta DEC = \Delta QRP\)(c.g.c) nên DE = QR ( 2 cạnh tương ứng)

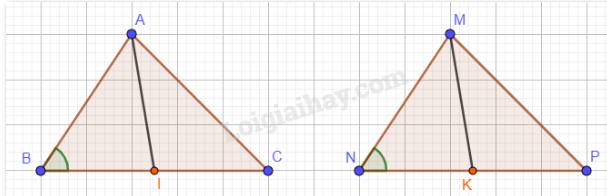
Hai tam giác ABC và MNP có: AB = MN, BC = NP, CA = PM nên \(\Delta ABC = \Delta MNP\)(c.c.c)
Suy ra: \(\widehat {ABI} = \widehat {MNK}\) ( 2 góc tương ứng).
Ta có: I, K lần lượt là trung điểm của BC và NP mà BC = NP, suy ra: \(BI = NK\).
Xét tam giác ABI và tam giác MNK có:
AB = MN;
\(\widehat {ABI} = \widehat {MNK}\);
BI = NK.
Vậy \(\Delta ABI = \Delta MNK\)(c.g.c). Suy ra: AI = MK (2 cạnh tương ứng).
Vậy AI = MK.

tự kẻ hình:3333
a) vì BE là phân giác của QBA=> B1=B2=QBA/2
vì BD là phân giác của ABC=> B3=B4=ABC/2
ta có EBD= B2+B3=QBA/2 +ABC/2= QBA+ABC/2= 180 độ/2=90 độ ( QBA kề bù với ABC)
trong tứ giác AEBD có EBD= 90 độ=> AEBD là HCN=> EBD=BDA=DAE=AEB= 90 độ
=> BEQ= 90 độ ( kề bù với AEB), BDP= 90 độ( kề bù với BDA)
=> BE vuông góc với AQ, BD vuông góc với AP
b)vì AEBD là hcn => AE=BD,
xét tam giác BEQ và tam giác BEA có
B1=B2(gt)
BE chung
BEQ=BEA(=90 độ)
=> tam giác BEQ= tam gáic BEA(gcg)
=> AE=EQ ( hai cạnh tương ứng)
ta có DBP+EBQ= 90 độ( EBD= 90 độ)
VÌ EBQ vuông tại E=> EQB+EBQ= 90 độ
=> DBP=EQB (=90 độ-EBQ)
xét tam giác BEQ và tam giác PDB có
EQ=BD(=AE)
BEQ=PDB(=90 độ)
DBP=EQB(cmt)
=> tam giác BEQ= tam gáic PDB(gcg)
=> QB=PB ( hai cạnh tương ứng)
=> B là trung điểm của PQ
c) xét tam giác AED và tam giác DBA có
AE=BD(cmt)
DAE=BDA(=90 độ)
AD chung
=> tam giác AED= tam giác DBA (cgc)
=> AB=DE( hai cạnh tương ứng)

a) Xét ΔAND và ΔCNB có
NA=NC(N là trung điểm của AC)
\(\widehat{AND}=\widehat{CNB}\)(hai góc đối đỉnh)
ND=NB(N là trung điểm của BD)
Do đó: ΔAND=ΔCNB(c-g-c)
b) Ta có: ΔAND=ΔCNB(cmt)
nên AD=BC(hai cạnh tương ứng)
Ta có: ΔAND=ΔCNB(cmt)
nên \(\widehat{ADN}=\widehat{CBN}\)(hai góc tương ứng)
mà \(\widehat{ADN}\) và \(\widehat{CBN}\) là hai góc ở vị trí so le trong
nên AD//BC(Dấu hiệu nhận biết hai đường thẳng song song)
a: ΔABC=ΔMNP
=>AB=MN; BC=NP; AC=MP; \(\widehat{BAC}=\widehat{NMP};\widehat{ABC}=\widehat{MNP};\widehat{ACB}=\widehat{MPN}\)
Ta có: BC=NP
mà \(BD=\dfrac{1}{2}BC;NQ=\dfrac{1}{2}NP\)
nên BD=NQ
Xét ΔABD và ΔMNQ có
AB=MN
\(\widehat{ABD}=\widehat{MNQ}\)
BD=NQ
Do đó: ΔABD=ΔMNQ
=>AD=MQ
b: Ta có: AC=MP
mà \(CE=\dfrac{1}{2}CA;PR=\dfrac{1}{2}PM\)
nên CE=PR
Xét ΔCED và ΔPRQ có
CE=PR
\(\widehat{ECD}=\widehat{RPQ}\)
CD=PQ
Do đó: ΔCED=ΔPRQ
=>DE=QR
Ta có △ 𝐴 𝐵 𝐶 = △ 𝑀 𝑁 𝑃 △ABC=△MNP, tức là chúng đồng dạng và có các cạnh tương ứng bằng nhau: 𝐴 𝐵 = 𝑀 𝑁 , 𝐵 𝐶 = 𝑁 𝑃 , 𝐶 𝐴 = 𝑃 𝑀 . AB=MN,BC=NP,CA=PM. Gọi 𝐷 , 𝐸 D,E lần lượt là trung điểm của 𝐵 𝐶 BC và 𝐶 𝐴 CA, đồng thời 𝑄 , 𝑅 Q,R là trung điểm của 𝑁 𝑃 NP và 𝑃 𝑀 PM. Ta cần chứng minh: a) 𝐴 𝐷 = 𝑀 𝑄 AD=MQ. b) 𝐷 𝐸 = 𝑄 𝑅 DE=QR. Chứng minh câu a: 𝐴 𝐷 = 𝑀 𝑄 AD=MQ Vì 𝐷 D là trung điểm của 𝐵 𝐶 BC và 𝑄 Q là trung điểm của 𝑁 𝑃 NP, ta xét đường trung tuyến 𝐴 𝐷 AD trong tam giác 𝐴 𝐵 𝐶 ABC và đường trung tuyến 𝑀 𝑄 MQ trong tam giác 𝑀 𝑁 𝑃 MNP. Do △ 𝐴 𝐵 𝐶 = △ 𝑀 𝑁 𝑃 △ABC=△MNP, nên các đường trung tuyến tương ứng cũng bằng nhau, suy ra: 𝐴 𝐷 = 𝑀 𝑄 . AD=MQ. Chứng minh câu b: 𝐷 𝐸 = 𝑄 𝑅 DE=QR Vì 𝐸 E là trung điểm của 𝐶 𝐴 CA và 𝑅 R là trung điểm của 𝑃 𝑀 PM, ta xét đoạn thẳng 𝐷 𝐸 DE trong tam giác 𝐴 𝐵 𝐶 ABC và đoạn 𝑄 𝑅 QR trong tam giác 𝑀 𝑁 𝑃 MNP. Trong △ 𝐴 𝐵 𝐶 △ABC, 𝐷 𝐸 DE là đường trung bình, nên: 𝐷 𝐸 = 1 2 𝐵 𝐶 . DE= 2 1 BC. Tương tự, trong △ 𝑀 𝑁 𝑃 △MNP, 𝑄 𝑅 QR là đường trung bình, nên: 𝑄 𝑅 = 1 2 𝑁 𝑃 . QR= 2 1 NP. Mà 𝐵 𝐶 = 𝑁 𝑃 BC=NP (do △ 𝐴 𝐵 𝐶 = △ 𝑀 𝑁 𝑃 △ABC=△MNP), nên suy ra: 𝐷 𝐸 = 𝑄 𝑅 . DE=QR. Kết luận: Ta đã chứng minh được: a) 𝐴 𝐷 = 𝑀 𝑄 AD=MQ. b) 𝐷 𝐸 = 𝑄 𝑅 DE=QR.