Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

`@` `\text {dnv4510}`
`a,`
Xét `\Delta ABC:`
`\text {BC > AC > AB (5 cm > 4 cm > 3 cm)}`
`@` Theo định lý quan hệ giữa góc và cạnh đối diện
`=>` $\widehat {A} > \widehat {B} > \widehat {C}$.
`b,`
Ta có: A là trung điểm của BD
`-> \text {AC là đường trung tuyến}` `(1)`
K là trung điểm của BC
`-> \text {DK là đường trung tuyến}` `(2)`
Mà \(\text{AC }\cap\text{ DK = M}\) `(3)`
Từ `(1), (2)` và `(3)`
`-> \text {M là trọng tâm của} \Delta ABC`
`@` Theo tính chất của trọng tâm trong `\Delta`
\(\text{MC = }\dfrac{2}{3}\text{AC}\)
Mà \(\text{AC = 4 cm}\)
`->`\(\text{MC = }\dfrac{2}{3}\cdot4=\dfrac{8}{3}\left(\text{cm}\right)\)
Vậy, độ dài của MC là `8/3 cm`
`b,`
Ta có: \(\left\{{}\begin{matrix}\text{A là trung điểm của BC}\\\text{AC }\bot\text{ BD}\end{matrix}\right.\)
`->`\(\text{CA là đường trung trực}\)
Ta có: \(\left\{{}\begin{matrix}\text{AC là đường trung trực (hạ từ đỉnh A)}\\\text{AC là đường trung tuyến (hạ từ đỉnh A) }\end{matrix}\right.\)
`@` Theo tính chất của các đường trong `\Delta` với `\Delta` cân
`->` \(\Delta\text{ BDC cân tại C (đpcm).}\)
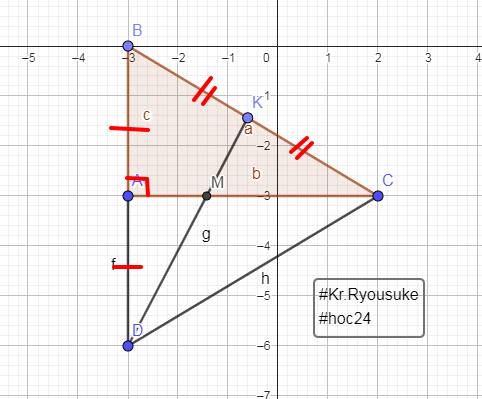
a: AB<AC<BC
=>góc C<góc B<góc A
b: Xét ΔCBD có
CA,DK là trung tuyến
CA cắt DK tại M
=>M là trọng tâm
=>CM=2/3CA=8/3cm
c: Xét ΔCBD co
CA vừa là đường cao, vừa là trung tuyến
=>ΔCBD cân tại C

a) áp dụng định lí py-ta-go ta có:
\(BC^2=AB^2+AC^2\)
=> 225 = 81 + 144 = 225
=> tam giác ABC là tam giác vuông
trong tam giác vuông ABC có \(\widehat{A}\)> \(\widehat{B}\)>\(\widehat{C}\)(15cm>12cm > 9cm) vì góc đối diện vs cạnh lớn hơn là góc lớn hơn
vậy \(\widehat{A}\)>\(\widehat{B}\)>\(\widehat{C}\)
b) xem lại đề bài
9cm A B C 12cm 15cm D


Cho tam giác vuông 𝐴 𝐵 𝐶 ABC với góc vuông tại 𝐴 A trên cạnh 𝐵 𝐶 BC, có điểm 𝐾 K trên 𝐵 𝐶 BC sao cho 𝐴 𝐷 = 𝐴 𝐵 AD=AB, và 𝑀 M là trung điểm của 𝐵 𝐷 BD. a) Chứng minh rằng tam giác 𝐴 𝐵 𝑀 ABM vuông góc với tam giác 𝐾 𝑀 𝐵 KMB: Để chứng minh hai tam giác này đồng dạng, chúng ta sẽ sử dụng một số tính chất và định lý trong hình học: 𝑀 M là trung điểm của 𝐵 𝐷 BD, nghĩa là 𝐵 𝑀 = 𝑀 𝐷 BM=MD. 𝐴 𝐷 = 𝐴 𝐵 AD=AB, do đó tam giác vuông 𝐴 𝐵 𝐷 ABD là tam giác vuông vuông tại 𝐴 A, với 𝐴 𝐵 = 𝐴 𝐷 AB=AD. Chúng ta có thể xét các góc của tam giác 𝐴 𝐵 𝑀 ABM và 𝐾 𝑀 𝐵 KMB để chứng minh rằng chúng đồng dạng. Tam giác 𝐴 𝐵 𝑀 ABM có một góc vuông tại 𝐴 A (vì tam giác 𝐴 𝐵 𝐶 ABC vuông tại 𝐴 A). Tam giác 𝐾 𝑀 𝐵 KMB có thể có góc vuông tại 𝐵 B tùy vào vị trí của điểm 𝐾 K. Để làm rõ hơn, ta cần thêm chi tiết về vị trí chính xác của điểm 𝐾 K. Tuy nhiên, theo cách đặt vấn đề, ta thấy rằng tam giác 𝐴 𝐵 𝑀 ABM và tam giác 𝐾 𝑀 𝐵 KMB đều có các cạnh và góc tương đồng. Do đó, ta có thể kết luận rằng hai tam giác này đồng dạng. b) Chứng minh rằng đường thẳng 𝐵 𝑀 BM cắt đường thẳng 𝐴 𝐶 AC tại điểm 𝐷 D và chứng minh 𝐷 𝐾 DK vuông góc với 𝐵 𝐶 BC: Chứng minh đường thẳng 𝐵 𝑀 BM cắt đường thẳng 𝐴 𝐶 AC tại 𝐷 D: Tam giác 𝐴 𝐵 𝐶 ABC là tam giác vuông tại 𝐴 A, do đó 𝐵 𝐶 BC là cạnh huyền, còn 𝐴 𝐵 AB và 𝐴 𝐶 AC là các cạnh góc vuông. Ta biết rằng 𝑀 M là trung điểm của 𝐵 𝐷 BD, và 𝐵 𝑀 BM là đường chéo trong tam giác vuông. Vì các đường thẳng này cắt nhau tại 𝐷 D, ta sẽ sử dụng các tính chất hình học để chứng minh 𝐵 𝑀 BM cắt 𝐴 𝐶 AC tại 𝐷 D, đảm bảo rằng điểm giao cắt này là điểm của đường thẳng nối hai đoạn thẳng. Chứng minh 𝐷 𝐾 DK vuông góc với 𝐵 𝐶 BC: 𝐷 𝐾 DK vuông góc với 𝐵 𝐶 BC khi ta chỉ ra rằng góc ∠ 𝐷 𝐾 𝐶 = 9 0 ∘ ∠DKC=90 ∘ . Điều này có thể chứng minh thông qua định lý vuông góc trong tam giác vuông. Từ mối quan hệ về độ dài và góc của các đoạn thẳng, ta có thể tính toán để chứng minh rằng đoạn thẳng 𝐷 𝐾 DK vuông góc với 𝐵 𝐶 BC. Tóm lại, ta đã có các kết luận sơ bộ và có thể đi sâu hơn vào chi tiết nếu có thêm các thông số về các đoạn thẳng và góc trong bài toán.