NT
5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
24 tháng 6 2017
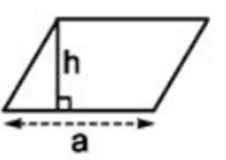
Hình bình hành là hình thang có hai đáy bằng nhau
⇒ Hình bình hành có cạnh đáy a và chiều cao h là:
S =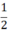 
h(a + a) = 
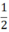h.2a = a.h
15 tháng 8
a: Ta có; \(AE=EB=\frac{AB}{2}\)
\(DF=FC=\frac{DC}{2}\)
mà AB=CD
nên AE=EB=DF=FC
Xét tứ giác AEFD có
AE//FD
AE=FD
Do đó: AEFD là hình bình hành
b: Xét tứ giác EFCB có
EB//CF
EB=CF
Do đó: EFCB là hình bình hành
c: Xét tứ giác DEBF có
BE//DF
BE=DF
Do đó: DEBF là hình bình hành
d: ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
Ta có: DEBF là hình bình hành
=>DB cắt EF tại trung điểm của mỗi đường
mà O là trung điểm của DB
nên O là trung điểm của EF
10 tháng 6 2016
Xét tam giác ADB có : M là trung điểm của AB(gt)
N là trung điểm của AD(gt)
=> MN là đường trung bình của tam giác ADB ( đ/n)
=> MN//DB và MN =1/2 DB ( t/c)
Xét tam giác AMN và tam giác ABD có : MN // BD ( cmt)
tam giác AMN đồng dạng với tam giác ABD ( hq đ/y ta lét) => SAMN/SABD=(1/2)^2=1/4 (1)
Xét tam giác ABD và tam giác CDBcó
AB=CD( ABCD là hbh )
góc A = góc C (nt)
AD=cb(nt)
=> tam giác ABD = tam giác CDB (cgc)
=> tam giác ABD đồng dạng tam giác CDB(t/c)
=> tam giác ABD=1/2 HBh ABCD(2)
Từ 1 2 => SAMN/SABCD=1/8
6 tháng 2 2022
Vẽ AH⊥BC⊥BC cắt MN tại H'
Ta có : AH'=HH'=12AH12AH(vì MN là trung điểm => AH′=12AHAH′=12AH)
Lại có:
SABC=12.AH.BC=60cm2SABC=12.AH.BC=60cm2 và SAMN=12AH′.MNSAMN=12AH′.MN.Mà
MN là đường trung bình của tam giác ABC=>MN=12BCMN=12BC
=>SAMN=12.12AH.12BC=14(12AH.BC)=12.60=15(cm2)SAMN=12.12AH.12BC=14(12AH.BC)=12.60=15(cm2)
Vậy SAMN=15cm2
28 tháng 7 2019
Tui chịu
B A C D F E I K M
K có đủ giữ liệu
Mới chả có góc nào thì tính kiểu j
Nếu ai k sai thì phải giải cho tui xem đóa
28 tháng 7 2019
Câu hỏi của Hoàng Ngọc Huyền - Toán lớp 8 - Học toán với OnlineMath
Ban tham khao nha !
TP
13 tháng 8
Lời giải: a) Chứng minh AE = DG
- Vì ABCD là hình bình hành nên ta có:
- AB // DC
- AB = DC
- Vì E là trung điểm của AB, ta có: \(A E = \frac{1}{2} A B\)
- Vì G là trung điểm của CD, ta có: \(D G = \frac{1}{2} D C\)
- Do AB = DC, nên \(\frac{1}{2} A B = \frac{1}{2} D C\).
- Suy ra, \(A E = D G\).
- Tứ giác có các cạnh đối song song.
- Tứ giác có các cạnh đối bằng nhau.
- Tứ giác có một cặp cạnh đối song song và bằng nhau.
- Ta đã có \(A E = D G\) (chứng minh ở câu a).
- Vì ABCD là hình bình hành nên AB // DC, suy ra AE // DG (vì E thuộc AB và G thuộc DC).
- Vì E là trung điểm của AB, ta có: \(A E = \frac{1}{2} A B\).
- Vì G là trung điểm của CD, ta có: \(C G = \frac{1}{2} C D\).
- Do ABCD là hình bình hành nên AB = CD.
- Từ đó suy ra, \(\frac{1}{2} A B = \frac{1}{2} C D\), tức là \(A E = C G\).
- Vì ABCD là hình bình hành nên AB // DC, suy ra AE // CG (vì E thuộc AB và G thuộc CD).
NT
13 tháng 8
Ta giải lần lượt như sau:
Giả thiết: ABCD là hình bình hành, E là trung điểm AB, G là trung điểm CD.
a) Chứng minh \(A E = D G\)
- Vì E là trung điểm AB ⇒ \(A E = \frac{1}{2} A B\)
- G là trung điểm CD ⇒ \(D G = \frac{1}{2} C D\)
- Trong hình bình hành: \(A B = C D\)
⇒ \(A E = D G\) (đpcm).
b) Chứng minh tứ giác AEGD là hình bình hành
- \(A E \parallel D G\) vì \(A E\) cùng phương với AB, còn AB ∥ DC ⇒ AE ∥ DG.
- \(A E = D G\) (chứng minh ở câu a).
- Trong tứ giác, nếu một cặp cạnh đối song song và bằng nhau ⇒ tứ giác đó là hình bình hành.
⇒ AEGD là hình bình hành (đpcm).
c) Chứng minh tứ giác AECG là hình bình hành
- Xét AC và EG:
- Trong hình bình hành ABCD, AC và BD cắt nhau tại trung điểm O ⇒ O là trung điểm AC.
- E và G lần lượt là trung điểm AB, CD ⇒ EG nối trung điểm AB và CD ⇒ EG ∥ AC và EG = AC.
- Vậy AC ∥ EG và AC = EG ⇒ AECG là hình bình hành (đpcm).
Nếu bạn muốn mình có thể vẽ hình minh họa để nhìn rõ các điểm E và G, bạn sẽ thấy các quan hệ song song và bằng nhau rất trực quan.
Bạn có muốn mình vẽ không?
S = a x h
S =a × h