Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Từ đề bài, ta có hình vẽ sau:
\(\hat{BAC}=\hat{BAH}+\hat{CAH}=10^0+10^0=20^0\)
Xét ΔABC có
AH là đường cao
AH là đường phân giác
Do đó: ΔABC cân tại A
=>\(\hat{ABC}=\frac{180^0-\hat{BAC}}{2}=\frac{180^0-20^0}{2}=80^0\)
Ta có: \(\hat{KBC}+\hat{KBA}=\hat{ABC}\) (tia BK nằm giữa hai tia BA và BC)
=>\(\hat{KBA}=80^0-40^0=40^0\)
Xét ΔABG và ΔACG có
AB=AC
\(\hat{BAG}=\hat{CAG}\)
AG chung
Do đó: ΔABG=ΔACG
=>\(\hat{ABG}=\hat{ACG}\)
=>\(x=40^0\)

a: Xét ΔABC có F,E lần lượt là trung điểm của AB,AC
=>FE là đường trung bình của ΔABC
=>FE//BC và \(FE=\frac12BC\)
=>BFEC là hình thang
Hình thang BFEC có \(\hat{FBC}=\hat{ECB}\) (ΔABC cân tại A)
nên BFEC là hình thang cân
b: Xét ΔABC có
F,D lần lượt là trung điểm của BA,BC
=>FD là đường trung bình của ΔABC
=>FD//AC và \(FD=\frac{AC}{2}\)
Xét ΔMAC có
I,K lần lượt là trung điểm của MA,MC
=>IK là đường trung bình củaΔMAC
=>IK//AC và \(IK=\frac{AC}{2}\)
Ta có: FD//AC
IK//AC
Do đó: FD//IK
Ta có: \(FD=\frac{AC}{2}\)
\(IK=\frac{AC}{2}\)
Do đó: FD=IK
Xét tứ giác FDKI có
FD//IK
FD=IK
Do đó: FDKI là hình bình hành
c: HK=HM+KM
\(=\frac12\cdot\left(MB+MC\right)=\frac12\cdot BC\)
=FE
Xét tứ giác FEKH có
FE//KH
FE=KH
Do đó: FEKH là hình bình hành
=>FK cắt EH tại trung điểm của mỗi đường(1)
FDKI là hình bình hành
=>FK cắt DI tại trung điểm của mỗi đường(2)
Từ (1),(2) suy ra FK,EH,DI đồng quy
d: ΔABC đều
mà AD là đường trung tuyến
nên AD là phân giác của góc BAC và AD⊥BC
=>\(\hat{BAD}=\frac12\cdot\hat{BAC}=\frac12\cdot60^0=30^0\)
Xét tứ giác APMD có \(\hat{APM}+\hat{ADM}=90^0+90^0=180^0\)
nên APMD là tứ giác nội tiếp đường tròn đường kính AM
=>APMD nội tiếp (I)
Xét (I) có \(\hat{PAD}\) là góc nội tiếp chắn cung PD
=>\(\hat{PID}=2\cdot\hat{PAD}=60^0\)
Xét ΔIPD có IP=ID và \(\hat{PID}=60^0\)
nên ΔIPD đều

1: \(\frac{1-a\cdot\sqrt{a}}{1-\sqrt{a}}=\frac{\left(1-\sqrt{a}\right)\left(1+\sqrt{a}+a\right)^{}}{1-\sqrt{a}}=1+\sqrt{a}+a\)
2: \(\frac{\sqrt{x+3}+\sqrt{x-3}}{\sqrt{x+3}-\sqrt{x-3}}=\frac{\left(\sqrt{x+3}+\sqrt{x-3}\right)\left(\sqrt{x+3}+\sqrt{x-3}\right)}{\left(\sqrt{x+3}-\sqrt{x-3}\right)\left(\sqrt{x+3}+\sqrt{x-3}\right)}\)
\(=\frac{\left(\sqrt{x+3}+\sqrt{x-3}\right)^2}{x+3-\left(x-3\right)}=\frac{x+3+x-3+2\sqrt{\left(x+3\right)\left(x-3\right)}}{6}\)
\(=\frac{2x+2\sqrt{x^2-9}}{6}=\frac{x+\sqrt{x^2-9}}{3}\)
4: \(\frac{3}{2\sqrt{9x}}=\frac{3}{2\cdot3\sqrt{x}}=\frac{1}{2\sqrt{x}}=\frac{\sqrt{x}}{2}\)
5: \(\frac{1}{2\sqrt{x}}=\frac{1\cdot\sqrt{x}}{2\sqrt{x}\cdot\sqrt{x}}=\frac{\sqrt{x}}{2x}\)
7: \(\frac{\sqrt{a^3}+a}{\sqrt{a}-1}=\frac{a\cdot\sqrt{a}+a}{\sqrt{a}-1}=\frac{a\left(\sqrt{a}+1\right)}{\sqrt{a}-1}=\frac{a\left(\sqrt{a}+1\right)\left(\sqrt{a}+1\right)}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}\)
\(=\frac{a\left(a+2\sqrt{a}+1\right)}{a-1}=\frac{a^2+2a\cdot\sqrt{a}+a}{a-1}\)
8: \(\frac{2}{\sqrt{a}+\sqrt{2b}}=\frac{2\cdot\left(\sqrt{a}-\sqrt{2b}\right)}{\left(\sqrt{a}+\sqrt{2b}\right)\left(\sqrt{a}-\sqrt{2b}\right)}=\frac{2\sqrt{a}-2\sqrt{2b}}{a-2b}\)
10: \(\frac{25}{\sqrt{a}-\sqrt{b}}=\frac{25\left(\sqrt{a}+\sqrt{b}\right)}{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}=\frac{25\sqrt{a}+25\sqrt{b}}{a-b}\)
11: \(-\frac{ab}{\sqrt{a}-\sqrt{b}}=-\frac{ab\left(\sqrt{a}+\sqrt{b}\right)}{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}=\frac{-ab\cdot\sqrt{a}-ab\cdot\sqrt{b}}{a-b}\)

10) đkxđ: \(x\ne\pm3\)
\(\frac{7}{a^2-9}+\frac{5}{a-3}+\frac{1}{a+3}=\frac{7}{\left(a-3\right)\left(a+3\right)}+\frac{5\cdot\left(a+3\right)}{\left(a+3\right)\left(a-3\right)}+\frac{a-3}{\left(a+3\right)\left(a-3\right)}\)
\(=\frac{7+5a+15+a-3}{\left(a+3\right)\left(a-3\right)}=\frac{6a+19}{\left(a+3\right)\left(a-3\right)}\)
11) đkxđ: \(x\ne-1\)
\(\frac{2x-1}{x^3+1}+\frac{2x}{x^2-x+1}-\frac{x}{x+1}+2\)
\(=\frac{2x-1}{\left(x+1\right)\left(x^2-x+1\right)}+\frac{2x\cdot\left(x+1\right)}{\left(x+1\right)\left(x^2-x+1\right)}-\frac{x\cdot\left(x^2-x+1\right)}{\left(x+1\right)\left(x^2-x+1\right)}+\frac{2\left(x+1\right)\left(x^2-x+1\right)}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(\) \(=\frac{2x-1+2x^2+2x-x^3+x^2-x+2x^3+2}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(=\frac{x^3+3x^2+3x+1}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(=\frac{\left(x+1\right)^3}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(=\frac{\left(x+1\right)^2}{x^2-x+1}\)
13) đkxđ: \(x\ne\pm\frac32\)
\(\frac{5}{2x-3}+\frac{2}{2x+3}-\frac{2x+5}{9-4x^2}\)
\(=\frac{5\cdot\left(2x+3\right)}{\left(2x-3\right)\left(2x+3\right)}+\frac{2\cdot\left(2x-3\right)}{\left(2x-3\right)\left(2x+3\right)}+\frac{2x+5}{\left(2x-3\right)\left(2x+3\right)}\)
\(=\frac{10x+15+4x-6+2x+5}{\left(2x-3\right)\left(2x+3\right)}\)
\(=\frac{16x+14}{\left(2x-3\right)\left(2x+3\right)}\)


a. áp dụnng định lý pythagore vào △ ABC vuông tại A ta có:
\(BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10\left(\operatorname{cm}\right)\)
b. diện tích △ ABC là:
\(\frac{6\cdot8}{2}=24\left(\operatorname{cm}^2\right)\)
c. ta có: \(BC\cdot AH=AB\cdot AC\)
\(\Rightarrow AH=\frac{AB\cdot AC}{BC}=\frac{6\cdot8}{10}=4,8\left(\operatorname{cm}\right)\)
áp dụng định lý pythagore vào △ ABH vuông tại H ta được:
\(HB=\sqrt{AB^2-AH^2}=\sqrt{6^2-4,8^2}=3,6\left(\operatorname{cm}\right)\)
áp dụng định lý pythagore vào △ AHC vuông tại H ta được:
\(HC=\sqrt{AC^2-AH^2}=\sqrt{8^2-4,8^2}=6,4\left(\operatorname{cm}\right)\)
d. vì M là trung điểm của cạnh BC
⇒ MB = MC = BC : 2 = 10 : 2 = 5 (cm)
ta có: BH + HM = BM
⇒ HM = BM - BH = 5 - 3,6 = 1,4 (cm)
áp dụng định lý pythagore vào △ AHM vuông tại H ta có:
\(AM=\sqrt{AH^2+HM^2}=\sqrt{4,8^2+1,4^2}=5\left(\operatorname{cm}\right)\)

a: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
=>\(HB=HC=\frac{BC}{2}=\frac{12}{2}=6\left(\operatorname{cm}\right)\)
ΔAHB vuông tại H
=>\(HA^2+HB^2=AB^2\)
=>\(HA^2=10^2-6^2=100-36=64=8^2\)
=>HA=8(cm)
b: Diện tích tam giác ABC là:
\(S_{ABC}=\frac12\cdot AH\cdot BC=\frac12\cdot12\cdot8=4\cdot12=48\left(\operatorname{cm}^2\right)\)

bạn lưu ảnh rồi gửi qua file đi ạ chứ bn cóp sang thì ko hiện ảnh mất rồi
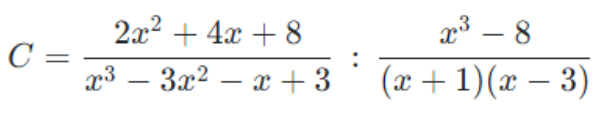








\(C=\frac{2\left(x^2+2x+4\right)}{\left(x-1\right)\left(x+1\right)\left(x-3\right)}.\frac{\left(x+1\right)\left(x-3\right)}{\left(x-2\right)\left(x^2+2x+4\right)}=\)
\(=\frac{2}{\left(x-1\right)\left(x-2\right)}\)
cảm ơn nhoa ✿