Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(SM=MA=SA-SM\Rightarrow SM=\dfrac{1}{2}SA\)
Do IM song song SO, áp dụng định lý Talet trong tam giác SAO:
\(\dfrac{IO}{OA}=\dfrac{SM}{SA}=\dfrac{1}{2}\)
Do NK song song SO, áp dụng định lý Talet cho tam giác SCO:
\(\dfrac{OK}{OC}=\dfrac{SN}{SC}=\dfrac{1}{3}\)
Mà ABCD là hình bình hành nên \(OA=OC\)
\(\Rightarrow\dfrac{OI}{OK}=\dfrac{3}{2}\)

Xét tam giác SAC, ta có M là trung điểm SA, O là trung điểm AC
\(\Rightarrow\) OM là đường trung bình tam giác SAC
\(\Rightarrow OM//SC\)
Mà \(O\in BD\Rightarrow OM\in\left(MBD\right)\)
\(\Rightarrow SC//\left(MBD\right)\)
Khi nhìn thấy dữ kiện tỉ lệ đoạn thẳng và yêu cầu song song thì ta nên nghĩ đến định lý Talet đảo hoặc đường trung bình (chúng sẽ dẫn tới việc chứng minh được các đoạn thẳng song song)

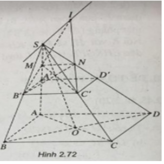
a) (P) // BC nên (P) sẽ cắt (SBC) theo giao tuyến B'C' song song với BC.
Tương tự, (P) cắt (SAD) theo giao tuyến MN song song với AD.
Khi M trùng với trung điểm A' của cạnh SA thì thiết diện MB'C'N' là hình bình hành.
b) Với M không trùng với A':
Gọi I ∈ B′M ∩ C′N. Ta có:
I ∈ B′M ⊂ (SAB), tương tự I′ ∈ C′N ⊂ (SCD)
Như vậy I ∈ Δ = (SAB) ∩ (SCD).

Trong mp (SAD), qua M kẻ đường thẳng song song AD cắt SA tại P
Trong mp (ABCD), qua N kẻ đường thẳng song song AD cắt AB tại Q
\(\Rightarrow PQ\in\left(\alpha\right)\)
Gọi E là giao điểm của AC và NQ
Trong mp (SAC), nối PE cắt SO tại K
\(\Rightarrow K=SO\cap\left(\alpha\right)\)

Mặt phẳng (P) qua A song song với BD nên (P) sẽ cắt (ABCD) theo giao tuyến d đi qua A và song song với BD. A và BD cố định nên d cố đinh

a) S là điểm chung của hai mặt phẳng (SAB) và (SCD) mà AB // CD
Từ S kẻ Sx sao cho Sx // AB // CD nên Sx là giao tuyến của hai mặt phẳng (SAB) và (SCD).
b) Gọi E là trung điểm của AB
G là trọng tâm tam giác SAB nên \(\frac{{EG}}{{SE}} = \frac{1}{3}\)
N là trọng tâm tam giác ABC nên\(\frac{{EN}}{{EC}} = \frac{1}{3}\)
Theo Ta lét, suy ra GN // SC mà SC \( \subset \) (SAC). Do đó, GN // (SAC)

Gọi G là giao của AC với DM
Xét △BCD có
MB=MC (gt); OB=OD (trong hbh 2 đường chéo cắt nhau tại trung điểm mối đường)
=> G là trọng tâm của △BCD
\(\rArr\frac{CG}{OC}=\frac23\) Mà \(OC=\frac{AC}{2}\rArr\frac{CG}{OC}=\frac{CG}{\frac{AC}{2}}=\frac{2CG}{AC}=\frac23\rArr\frac{CG}{AC}=\frac13\rArr\frac{CG}{GA}=\frac12\)
Xét △SAC có
\(\frac{CG}{GA}=\frac12\left(\operatorname{cm}t\right)\)
\(NS=2NC\rArr\frac{NC}{NS}=\frac12\)
\(\rArr\frac{CG}{GA}=\frac{NC}{NS}\) => SA//NG (Talet đảo)
Mà NG∈(DMN) => SA//(DMN)