Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a, Vì AM = BM ( tc tiếp tuyến )
OA = OB = R
Vậy OM là đường trung trực đoạn AB hay OM vuông AB tại H
b, Vì MA là tiếp tuyến => ^OAM = 900
Xét tam giác OAM vuông tại A, đường cao AH
Ta có : \(AO^2=OH.OM\)( hệ thức lượng )
\(\Rightarrow R^2=OH.OM\)
c, Ta có ^ABD = 900 ( góc nt chắn nửa đường tròn )
=> AB vuông BD và AB vuông OM ( cmt )
=> BD // OM ( tc vuông góc đến song song )
d, gợi ý : có OH vuông AB => H là trung điểm
-> chỉ ra NH // AE
=> N là trung điểm ( theo tc đường trung bình )
Lời giải:
1. Vì $MA, MB$ là tiếp tuyến của $(O)$ nên $MA\perp OA, MB\perp OB$.
Khi đó $\widehat{MAO}=\widehat{MBO}=90^0$
Tứ giác $MAOB$ có tổng 2 góc đối nhau $\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0$
$\Rightarrow MAOB$ là tứ giác nội tiếp.
$\Rightarrow M,A,O,B$ cùng thuộc 1 đường tròn.
2.
Có: $MA=MB, OA=OB$ nên $MO$ là trung trực của $AB$
$\Rightarrow MO\perp AB$ tại $C$.
Xét tam giác $MOB$ vuông tại $B$ có đường cao $BC$. Áp dụng hệ thức lượng trong tam giác vuông thì:
$MC.MO=MB^2(1)$
Xét tam giác $MQB$ và $MBD$ có:
$\widehat{M}$ chung
$\widehat{MBQ}=\widehat{MDB}$ (góc tạo bởi tiếp tuyến và dây cung bằng góc nội tiếp chắn cung đó)
$\Rightarrow \triangle MQB\sim \triangle MBD$ (g.g)
$\Rightarrow \frac{MQ}{MB}=\frac{MB}{MD}$
$\Rightarrow MQ.MD=MB^2(2)$
Từ $(1); (2)\Rightarrow MQ.MD=MC.MO$
a: OH*OM=OA^2=R^2
b: ΔOCD cân tại O
mà OI là đường trung tuyến
nên OI vuông góc với CD
Xét tứ giác OIAM có
góc OIM=góc OAM=90 độ
nên OIAM là tứ giác nội tiếp
c: Xét ΔOHK vuông tại H và ΔOIM vuông tại I có
góc HOK chung
Do đo: ΔOHK đồng dạng với ΔOIM
=>OH/OI=OK/OM
=>OI*OK=OH*OM=R^2=OC^2
mà CI vuông góc với OK
nên ΔOCK vuông tại C
=>KC là tiếp tuyến của (O)
a) góc HEC = góc CAM = góc CBH.
b) CM EB2 = EC.EA = EM2 từ đó ta có góc EMC = góc EAM = góc ADC suy ra AD song song MB. Do đó góc BDA = góc ABM = góc BAD.
c) Ta có BJ là đường kính và BJ vuông góc với AD tại K (AD song song MB). Do đó KD = KA
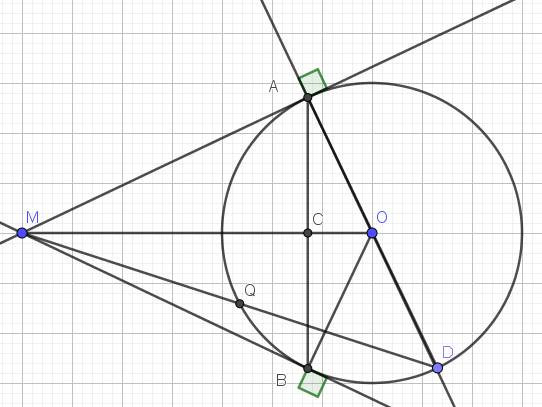
M A B D H C
a/
Xét tg vuông OAM và tg vuông OBM
OA = OB = R
OM chung
=> tg OAM = tg OBM (2 tg vuông có cạnh huyền và cạnh góc vuông tương ứng = nhau)
=> MA = MB => tg MAB cân tại M và ^OMA = ^OMB
=> OM vuông góc với AB (trong tg cân đường phân giác của góc ở đỉnh đồng thời là đường cao)
b/
Ta có
^ACD = 90o (góc nt chắn nửa đường tròn) => AC vg với MD
OM vg với AB (cmt)
=> H và C cùng nhìn MA dưới 2 góc = nhau và = 90o
=> H và C cùng nằm trên đường tròn đường kính MA => A; H; C; M cùng nằm trên 1 đường tròn
c/
Xét tứ giác nt AHCM có
^AMC + ^AHC = 180o (trong tứ giác nt tổng 2 góc đối nhau = 180o)
^CHB + ^AHC = ^AHB = 180o
=> ^CHB = ^AMC => sinCHB = sinAMC
Xét tg vuông AMC có
cosAMC = MC/MA
sinCHB = sinAMC = AC/MA
=> cosAMC . sinCHB = MC.AC/MA2
Xét tg vuông AMD
MA2 = MC.DM (trong tg vuông bình phương 1 cạnh góc vuông băng tích giữa hình chiếu cạnh góc vuông đó trên cạnh huyền với cạnh huyền)
=> cosAMC . sinCHB = MC.AC/MC.DM
=> AC = DM.cosAMC . sinCHB