Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b) Xét tứ giác BFEC có:
∠(BFC) = 90 0 (Do CF là đường cao)
∠(BEC ) = 90 0 (Do BE là đường cao)
⇒ E và F cùng nhìn BC dưới một góc bằng nhau
⇒ Tứ giác BFEC nội tiếp được đường tròn
⇒ Bốn điểm B, E, F, C cùng nằm trên đường tròn

a: Xét (O) có
ΔABM nội tiếp
AM là đường kính
Do đó: ΔABM vuông tại B
=>BM\(\perp\)AB
mà CH\(\perp\)AB
nên CH//BM
Xét (O) có
ΔACM nội tiếp
AM là đường kính
Do đó: ΔACM vuông tại C
=>AC\(\perp\)CM
mà BH\(\perp\)AC
nên BH//CM
Xét tứ giác BHCM có
BH//CM
BM//CH
Do đó: BHCM là hình bình hành
b:
Xét ΔABC có
BE,CF là các đường cao
BE cắt CF tại H
Do đó: H là trực tâm của ΔABC
=>AH\(\perp\)BC tại D
Xét (O) có
\(\widehat{ABC}\) là góc nội tiếp chắn cung AC
\(\widehat{AMC}\) là góc nội tiếp chắn cung AC
Do đó: \(\widehat{ABC}=\widehat{AMC}\)
Ta có: \(\widehat{ABC}+\widehat{BAN}=90^0\)(ΔADB vuông tại D)
\(\widehat{AMC}+\widehat{MAC}=90^0\)(ΔACM vuông tại C)
mà \(\widehat{ABC}=\widehat{AMC}\)
nên \(\widehat{BAN}=\widehat{MAC}\)
Xét (O) có
ΔANM nội tiếp
AM là đường kính
Do đó: ΔANM vuông tại N
=>AN\(\perp\)NM
mà AN\(\perp\)BC
nên BC//NM
Ta có: \(\widehat{CHD}=\widehat{ABC}\)(=90 độ-góc FCB)
\(\widehat{ABC}=\widehat{ANC}\)
Do đó: \(\widehat{CHD}=\widehat{ANC}\)
=>ΔCHN cân tại C
=>CH=CN
mà CH=BM
nên BM=CN
Xét tứ giác BCMN có BC//MN
nên BCMN là hình thang
Hình thang BCMN có BM=CN
nên BCMN là hình thang cân

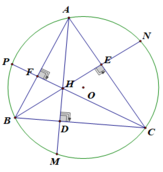
Đường tròn c: Đường tròn qua B_1 với tâm O Đoạn thẳng f: Đoạn thẳng [A, B] Đoạn thẳng g: Đoạn thẳng [A, C] Đoạn thẳng h: Đoạn thẳng [B, C] Đoạn thẳng l: Đoạn thẳng [P, C] Đoạn thẳng m: Đoạn thẳng [M, A] Đoạn thẳng n: Đoạn thẳng [B, N] O = (1.97, 2.92) O = (1.97, 2.92) O = (1.97, 2.92) Điểm A: Điểm trên c Điểm A: Điểm trên c Điểm A: Điểm trên c Điểm B: Điểm trên c Điểm B: Điểm trên c Điểm B: Điểm trên c Điểm C: Điểm trên c Điểm C: Điểm trên c Điểm C: Điểm trên c Điểm P: Giao điểm của c, j Điểm P: Giao điểm của c, j Điểm P: Giao điểm của c, j Điểm M: Giao điểm của c, k Điểm M: Giao điểm của c, k Điểm M: Giao điểm của c, k Điểm N: Giao điểm của c, i Điểm N: Giao điểm của c, i Điểm N: Giao điểm của c, i Điểm F: Giao điểm của j, f Điểm F: Giao điểm của j, f Điểm F: Giao điểm của j, f Điểm E: Giao điểm của i, g Điểm E: Giao điểm của i, g Điểm E: Giao điểm của i, g Điểm D: Giao điểm của k, h Điểm D: Giao điểm của k, h Điểm D: Giao điểm của k, h Điểm H: Giao điểm của l, m Điểm H: Giao điểm của l, m Điểm H: Giao điểm của l, m
a. Tứ giác CEHD có \(\widehat{HEC}=\widehat{HDC}=90^o\Rightarrow\) nó là tứ giác nội tiếp.
b. Tứ giác BFEC có \(\widehat{BEC}=\widehat{BFC}=90^o\Rightarrow\)nó là tứ giác nội tiếp. Vậy 4 điểm B, C, E, F cùng thuộc một đường tròn.
c. Ta thấy \(\Delta HAE\sim\Delta CAD\left(g-g\right)\Rightarrow\frac{AH}{AC}=\frac{AE}{AD}\Rightarrow AE.AC=AH.AD\)
Ta thấy \(\Delta CBE\sim\Delta CAD\left(g-g\right)\Rightarrow\frac{BC}{AC}=\frac{BE}{AD}\Rightarrow AD.BC=BE.AC\)
d. Ta thấy ngay \(\widehat{PCB}=\widehat{BAM}\) (Cùng phụ với góc ABC)
Mà \(\widehat{BAM}=\widehat{BCM}\) (Góc nội tiếp cùng chắn cung BM)
Vậy nên \(\widehat{PCB}=\widehat{BCM}\) hay CM là phân giác góc \(\widehat{PCB}\)
Lại có \(CM⊥HD\) nên HCM là tam giác cân. Vậy CB là trung trực của HM hay H, M đối xứng nhau qua BC.
e. Ta thấy BFHD là tứ giác nội tiếp nên \(\widehat{FDH}=\widehat{FBH}\) (Góc nội tiếp cùng chẵn cung FH)
DHEC cùng là tứ giác nội tiếp nên \(\widehat{HDE}=\widehat{HCE}\) (Góc nội tiếp cùng chẵn cung HE)
Mà \(\widehat{FBH}=\widehat{HCE}\) ( Cùng phụ với góc \(\widehat{BAC}\) )
nên \(\widehat{FDH}=\widehat{HDE}\) hay DH là phân giác góc FDE.
Tương tự FH, EH cũng là phân giác góc DFE và DEF.
Vậy tâm đường tròn nội tiếp tam giác DEF chính là H.

a: Xét tứ giác BEFC có \(\widehat{BEC}=\widehat{BFC}=90^0\)
nên BEFC là tứ giác nội tiếp đường tròn đường kính BC
=>B,E,F,C cùng thuộc một đường tròn
tâm I là trung điểm của BC
b: Xét ΔABC có
BF,CE là các đường cao
BF cắt CE tại H
Do đó: H là trực tâm của ΔABC
=>AH\(\perp\)BC
=>AM\(\perp\)BC
Xét (O) có
ΔAMD nội tiếp
AD là đường kính
Do đó: ΔAMD vuông tại M
=>AM\(\perp\)MD
Ta có: AM\(\perp\)BC
AM\(\perp\)MD
Do đó: BC//MD
Xét (O) có
\(\widehat{ABC}\) là góc nội tiếp chắn cung AC
\(\widehat{ADC}\) là góc nội tiếp chắn cung AC
Do đó: \(\widehat{ABC}=\widehat{ADC}\)
Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đó: ΔACD vuông tại C
Ta có: \(\widehat{BAH}+\widehat{ABC}=90^0\)(AH\(\perp\)BC)
\(\widehat{ADC}+\widehat{CAD}=90^0\)(ΔACD vuông tại C)
mà \(\widehat{ABC}=\widehat{ADC}\)
nên \(\widehat{BAH}=\widehat{CAD}\)
=>\(\widehat{BAH}+\widehat{MAD}=\widehat{CAD}+\widehat{MAD}\)
=>\(\widehat{BAD}=\widehat{CAM}\)(1)
Xét (O) có
\(\widehat{BAD}\) là góc nội tiếp chắn cung BD
\(\widehat{BCD}\) là góc nội tiếp chắn cung BD
Do đó: \(\widehat{BAD}=\widehat{BCD}\left(2\right)\)
Xét (O) có
\(\widehat{CBM}\) là góc nội tiếp chắn cung CM
\(\widehat{CAM}\) là góc nội tiếp chắn cung CM
Do đó: \(\widehat{CBM}=\widehat{CAM}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\widehat{CBM}=\widehat{BCD}\)
Xét tứ giác BCDM có BC//DM
nên BCDM là hình thang
Hình thang BCDM có \(\widehat{CBM}=\widehat{BCD}\)
nên BCDM là hình thang cân
c: Xét (O) có
ΔABD nội tiếp
AD là đường kính
Do đó: ΔABD vuông tại B
=>BA\(\perp\)BD
mà CH\(\perp\)BA
nên CH//BD
Ta có: CD\(\perp\)CA
BH\(\perp\)AC
Do đó: BH//CD
Xét tứ giác BHCD có
BH//CD
BD//CH
Do đó: BHCD là hình bình hành
=>BC cắt HD tại trung điểm của mỗi đường
mà I là trung điểm của BC
nên I là trung điểm của HD
=>H,I,D thẳng hàng
d: Kẻ tiếp tuyến Ax của (O)
Xét (O) có
\(\widehat{xAC}\) là góc tạo bởi tiếp tuyến Ax và dây cung AC
\(\widehat{ABC}\) là góc nội tiếp chắn cung AC
Do đó: \(\widehat{xAC}=\widehat{ABC}\)
mà \(\widehat{ABC}=\widehat{AFE}\left(=180^0-\widehat{EFC}\right)\)
nên \(\widehat{xAC}=\widehat{AFE}\)
mà hai góc này là hai góc ở vị trí so le trong
nên EF//Ax
Ta có: Ax//EF
Ax\(\perp\)AD
Do đó: AD\(\perp\)EF tại K

Đáp án:
Giải thích các bước giải:
1. Xét tứ giác CEHD có :
CEH = 90 ( BE là đường cao )
CDH = 90 ( AD là đường cao )
⇒ CEH + CDH = 90 + 90 = 180
Mà CEH và CDH là hai góc đối của tứ giác CEHD
⇒ CEHD là tứ giác nội tiếp (đpcm)
2. BE là đường cao ( gt )
⇒ BE ⊥ AB ⇒ BFC = 90
Như vậy E và F cùng nhìn BC dưới một góc 90 ⇒ E và F cùng nằm trên (O) đường kính AB
⇒ 4 điểm B, C, E, F cùng nằm trên một đường tròn (đpcm)
3. Xét ΔAEH và ΔADC có :
AEH = ADC (=90)
A chung
⇒ ΔAEH ~ ΔADC
⇒ AE/AD = AH/AC
⇒ AE.AC = AH.AD
Xét ΔBEC và ΔADC có :
BEC = ADC (=90)
C chung
⇒ ΔBEC ~ ΔADC
⇒ AE/AD = BC/AC
⇒ AD.BC = BE.AC (đpcm)
4. Có : C1 = A1 (cùng phụ góc ABC)
C2 = A1 ( hai góc nối tiếp chắn cung BM )
⇒ C1 = C2 ⇒ CB là tia phân giác HCM
Lại có : CB ⊥ HM
⇒ Δ CHM cân tại C
⇒ CB là đường trung trực của HM
⇒ H và M đối xứng nhau qua BC (đpcm)
5. Có : Bốn điểm B,C,E,F cùng nằm trên một đường tròn ( câu 2 )
⇒ C1 = E1 (hai góc nội tiếp cùng chắn BF) (*)
Có : Tứ giác CEHD nội tiếp (câu 1)
⇒ C1 = E2 (hai góc nội tiếp cùng chắn cung HD ) (**)
Từ (*) và (**) ta suy ra :
E1 = E2
⇒ EB là tia phân giác DEF
Cm tương tự ta được : FC là tia phân giác của DFE
Mà BE và CF cắt nhau tại H
⇒ H là tâm của đường tròn nội tiếp ΔDEF


Xét tứ giác CEHD ta có:
Góc CEH = 900 (Vì BE là đường cao)
Góc CDH = 900 (Vì AD là đường cao)
=> góc CEH + góc CDH = 1800
Mà góc CEH và góc CDH là hai góc đối của tứ giác CEHD. Do đó CEHD là tứ giác nội tiếp.
Chúng ta cần chứng minh rằng:
∠DBE=∠DAC=∠DBH\angle DBE = \angle DAC = \angle DBH Chứng minh góc ∠DBE=∠DAC\angle DBE = \angle DAC:-
-
-
∠DAC=∠DBE (goˊc cuˋng cha˘ˊn cung DE trong đường troˋn O)\angle DAC = \angle DBE \text{ (góc cùng chắn cung DE trong đường tròn O)} Chứng minh góc ∠DAC=∠DBH\angle DAC = \angle DBH:Vì A,B,CA, B, C là các điểm trên đường tròn (O), các tam giác ABCABC và ADEADE đều là các tam giác nội tiếp.
ADAD là đường cao từ AA tới BCBC nên ∠ADE\angle ADE = 90 độ.
Vậy:
-
-
∠DBE=∠DBH (goˊc tạo bởi đường cao từ đỉnh vaˋ goˊc tạo bởi hai đường cao ca˘ˊt nhau tại H trong đường troˋn)\angle DBE = \angle DBH \text{ (góc tạo bởi đường cao từ đỉnh và góc tạo bởi hai đường cao cắt nhau tại H trong đường tròn)}Từ chứng minh trên, ta đã có ∠DAC=∠DBE\angle DAC = \angle DBE
Ta có BFBF là đường cao từ BB tới ACAC, do đó:
-
∠DAC=∠DBE=∠DBH\angle DAC = \angle DBE = \angle DBHVậy:
Ta đã chứng minh được rằng: ∠DBE=∠DAC=∠DBH\angle DBE = \angle DAC = \angle DBH.
Nếu bạn có bất kỳ thắc mắc nào khác hoặc cần giải thích thêm, mình luôn sẵn sàng giúp đỡ! 😊