Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

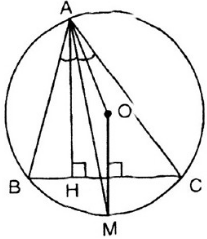
a) Ta có AP là tia phân giác của \(\widehat{BAC}\)
=> \(\widehat{BAP}=\widehat{PAC}\)
=> \(\stackrel\frown{BP}=\stackrel\frown{PC}\) (2 góc nt bằng nhau chắn 2 cung bằng nhau)=> P nằm chính giữa \(\stackrel\frown{BC}\)
=> BP=PC
Ta có OB = OC = R
=> O thuộc đường trung trực của BC
Lại có BP = PC => P thuộc đường trung trực của BC
=> OP là đường trung trực của BC
=> OP vuông góc với BC (1)
Lại có AH là đường cao từ A của tam giác ABC
=> AH vuông góc với BC (2)
Từ 1 và 2 => OP //AH
b) Ta có OA = OP = R
=> \(\widehat{OAP}=\widehat{OPA}\) (2 góc ở đáy )
Mà \(\widehat{OPA}=\widehat{HAP}\) (do AH//OP)
=> \(\widehat{HAP}=\widehat{OAP}\), mà AP nằm giữa AH và AO
=> AP là tia phân giáccuar góc OAH

O A B C P H
a) Xét đường tròn (O;R) có \(\widehat{CAP}=\widehat{BAP}\) (do AP là phân giác \(\widehat{BAC}\))
=> \(\stackrel\frown{CP}=\stackrel\frown{BP}\) (hai góc nội tiếp bằng nhau chắc hai cung bằng nhau)
=> CP = BP (liên hệ giữa cung và dây)
Lại có OB = OC = R => OP là trung trực của BC hay OP ⊥ BC.
Mà AH ⊥ BC (gt) => OP // AH
b) (Chắc bài hỏi AP là phân giác góc OAH đúng không bạn)
Xét đương tròn (O;R) có OA = OP = R => ΔOAP cân tại O
=> \(\widehat{OAP}=\widehat{OPA}\)
Do OP // AH (cmt) => \(\widehat{HAP}=\widehat{OPA}\) (slt)
=> \(\widehat{OAP}=\widehat{HAP}\left(=\widehat{OPA}\right)\)
=> AP là phân giác \(\widehat{OAH}\)

- OP // AH VÌ CÙNG VUÔNG GÓC VỚI BC
- VÌ OP//AH => \(\widehat{PAH}=\widehat{APO}\)LẠI CÓ : \(\widehat{APO}=\widehat{PAO}\)\(\Rightarrow\widehat{PAH}=\widehat{PAO}\)
NÊN AP LÀ P/G
Kéo dài AO cắt (O) tại D
C/m: tgiac ADC vuông tại D
góc ABH = góc ADC (cùng chắn cung AC)
góc ABH + BAH = góc ADC + góc DAC (= 900)
suy ra: góc BAH = góc DAC
mà góc BAP = góc CAP
suy ra: góc HAP = góc DAP
mà góc DAP = góc OPA
=> góc HAP = góc OPA
=> OP // AH
góc HAP = góc DAP (cmt)
=> AP là phân giác góc OAH
=> AP là phân giác

B1, a, Xét tứ giác AEHF có: góc AFH = 90o ( góc nội tiếp chắn nửa đường tròn)
góc AEH = 90o (góc nội tiếp chắn nửa đường tròn )
Góc CAB = 90o ( tam giác ABC vuông tại A)
=> tứ giác AEHF là hcn(đpcm)
b, do AEHF là hcn => cũng là tứ giác nội tiếp => góc AEF = góc AHF ( hia góc nội tiếp cùng chắn cung AF)
mà góc AHF = góc ACB ( cùng phụ với góc FHC)
=> góc AEF = góc ACB => theo góc ngoài tứ giác thì tứ giác BEFC là tứ giác nội tiếp (đpcm)
c,gọi M là giao điểm của AI và EF
ta có:góc AEF = góc ACB (c.m.t) (1)
do tam giác ABC vuông tại A và có I là trung điểm của cạng huyền CB => CBI=IB=IA
hay tam giác IAB cân tại I => góc MAE = góc ABC (2)
mà góc ACB + góc ABC + góc BAC = 180o (tổng 3 góc trong một tam giác)
=> ACB + góc ABC = 90o (3)
từ (1) (2) và (3) => góc AEF + góc MAE = 90o
=> góc AME = 90o (theo tổng 3 góc trong một tam giác)
hay AI uông góc với EF (đpcm)



A B C P H O
a/
\(sđ\widehat{BAP}=\dfrac{1}{2}sđcungBP\) (góc nt)
\(sđ\widehat{CAP}=\dfrac{1}{2}sđcungCP\) (góc nt)
Mà \(\widehat{BAP}=\widehat{CAP}\left(gt\right)\)
\(\Rightarrow sđcungBP=sđcungCP\)
\(sđ\widehat{BOP}=sđcungBP\) (góc ở tâm)
\(sđ\widehat{COP}=sđcungCP\) (góc ở tâm)
\(\Rightarrow\widehat{BOP}=\widehat{COP}\)
Xét \(\Delta BOC\)
\(OB=OC\) (bán kính (O)) => \(\Delta BOC\) cân tại O
\(\widehat{BOP}=\widehat{COP}\left(cmt\right)\)
\(\Rightarrow OP\perp BC\) (trong tg cân đường phân giác của góc ở đỉnh đồng thời là đường cao)
\(AH\perp BC\left(gt\right)\)
=> OP//AH (cung vg với BC)
b/
Xét \(\Delta OAC\)
\(OA=OC\) (bán kính (O)) \(\Rightarrow\Delta OAC\) cân tại O
\(\Rightarrow\widehat{OAP}=\widehat{OPA}\) (góc ở đáy tg cân)
OP//AH (cmt) \(\Rightarrow\widehat{HAP}=\widehat{OPA}\) (góc so le trong)
\(\Rightarrow\widehat{OAP}=\widehat{HAP}\) (cùng \(=\widehat{OPA}\) )
=> AP là phân giác của \(\widehat{OAH}\)