3M
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
BD
25 tháng 10 2016
Tổng số phần bằng nhau :
4 + 1 = 5 ( phần )
Giá trị 1 phần cũng là chiều rộng :
60 : 5 = 12 ( cm )
Chiều dài hình chữ nhật :
12 x 4 = 48 ( cm )
đ/s : 12 cm và 48 cm
25 tháng 10 2016
ta có sơ đồ : chiều dài : |===|===|===|===|
chiều rộng : |===| tổng : 60 cm
tổng số phần bằng nhau là :
4 + 1 = 5 ( phần )
chiều dài HCN là :
60 : 5 x 4 = 48 ( cm )
chiều rộng HCN là :
60 : 5 = 12 ( cm )
ĐS : ....
NH
12 tháng 2 2016
a/ Xét tam giác ABE và ACD:
Góc A: chung
AB=AC (gt)
AE=AD ( do AB= AC nên trung điểm của AB=AC bằng nhau)
=> Hai tam giác ABE=ACD ( c.g.c)
b/ Do tam giác ABE=ACD nên BE= CD ( hai cạnh tương ứng)
c/ Do góc ABC= ACB ( ABC cân A)
-> Góc ABE=ACE ( do ABE=ACD)
=> ABC-ABE=ACB-ACE
Vậy: Tam giác KBC cân K ( do góc KBC=KCB)
d/ Bạn tự làm nhé, vẽ hình ra rồi làm, ở đây vẽ hình là đợi duyệt lâu lắm
12 tháng 2 2016
Xét tam giác ABE và tam giác ACD có:
góc A chung
AB=AC(tam giác ABC cân tại A)
AD=AE(trung điểm của 2 cạnh bằng nhau)
=> tam giác ABE=tam giác ACD(c-g-c)
9 tháng 5 2023
\(S_{Xq}=\left(12+8+\sqrt{12^2+8^2}\right)\cdot10=\left(20+4\sqrt{13}\right)\cdot10\left(cm^2\right)\)
TG
7 tháng 11 2019
A B C M
- Vẽ hình ko chính xác cho lắm!
Giải
a/ Xét ΔABM và ΔACM ta có:
AB = AC (GT)
AM: cạnh chung
MB = MC (GT)
=> ΔABM = ΔACM (c - c - c)
=> \(\widehat{AMB}=\widehat{AMC}\)
Lại có: \(\widehat{AMB}\) + \(\widehat{AMC}\) = 1800 (kề bù)
=> \(\widehat{AMB}=\widehat{AMC}\) = 1800 : 2 = 900
=> AM ⊥ BC
VM
6 tháng 11 2019
a) Xét 2 \(\Delta\) \(ABM\) và \(ACM\) có:
\(AB=AC\left(gt\right)\)
\(BM=CM\) (vì M là trung điểm của \(BC\))
Cạnh AM chung
=> \(\Delta ABM=\Delta ACM\left(c-c-c\right).\)
b) Theo câu a) ta có \(\Delta ABM=\Delta ACM.\)
=> \(\widehat{BAM}=\widehat{CAM}\) (2 góc tương ứng)
=> \(AM\) là tia phân giác của \(\widehat{BAC}.\)
c) Xét \(\Delta ABC\) có:
\(AB=AC\left(gt\right)\)
=> \(\Delta ABC\) cân tại A.
Có \(AM\) là đường phân giác (cmt).
=> \(AM\) đồng thời là đường cao của \(\Delta ABC.\)
=> \(AM\perp BC\left(đpcm\right).\)
Chúc bạn học tốt!
21 tháng 11 2019
Xét \(\Delta\)OAD và \(\Delta\)OBD có :
OD : cạnh chung
OÂD = Góc OBD ( = 90° )
AÔD = BÔD ( vì Oz là phân giác của xÔy )
\(\Rightarrow\)\(\Delta\)OAD = \(\Delta\)OBD ( cạnh huyền - góc nhọn )
\(\Rightarrow\)AD = BD ( 2 cạnh tương ứng )
\(\Rightarrow\)D là trung điểm AB
21 tháng 11 2019
cậu làm hộ mình câu tiếp theo của bài này nhé!
2.Qua D kẻ đường thẳng vuông góc với tia Ox tại M cắt tia Oy tại F.Qua D kẻ đường thẳng vuông góc với tia Oy tại N cắt tia Ox tại E.CM rằng:
a,DB là tia p/g của \(\widehat{NDF}\)
b,MN // AB
NHỚ TÍCH CHO MK. ^^
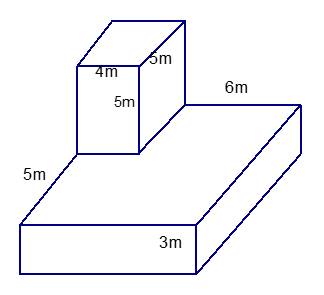
Mỗi mặt bên của hình lăng trụ đứng là một hình chữ nhật.
Giải thích:
Ví dụ:
\(-\) Tất cả những mặt bên của hình lăng trụ đứng là hình chữ nhật.
\(-\) Những mặt phẳng chứa đáy song song với nhau.