Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương pháp giải
Sử dụng: Trong tam giác vuông, cạnh góc vuông bằng cạnh góc vuông kia nhân tan góc đối.

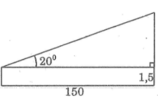
Đặt tên như hình vẽ thì chiều cao của tháp là đoạn BDBD
Xét tam giác ABCABC vuông tại AA có AC=DE=150m;ˆC=200AC=DE=150m;C^=200 nên
AB=150.tan20∘≈54,596(m)AB=150.tan20∘≈54,596(m)
Chiều cao của cột ăng-ten là:
BD=AB+ADBD=AB+AD=54,596+1,5=56,096(m).

- Xét ΔABC vuông tại A, áp dụng hệ thức c - góc ta có:
AC = \(\frac{AB}{tanC}\) = \(\frac{150}{tan20^0}\) =412,12 m
Vậy chiều cao của tháp là 412, 12 m

Phần còn lại của cột ăng-ten là cạnh đối của góc 20 ° , khoảng cách từ chỗ em đứng đến chân cột ăng-ten là cạnh kề với góc 20 °
Phần còn lại của cột ăng-ten cao là:
150.tg 20 ° ≈ 54,596 (m)
Chiều cao của cột ăng-ten là:
54,596 + 1,5 = 56,096 (m)

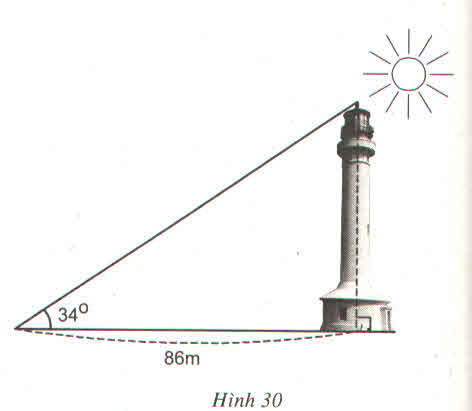
Gọi a là chiều cao của tháp, ta có:
\(\tan34\) = \(\dfrac{c.đối}{c.kề}\)= \(\dfrac{a}{86}\)
\(\Rightarrow a=\) \(\tan34.86\) \(\approx\) 58m
Vậy chiều cao của tháp là 58m


Vẽ lại hình:
Ta có: ABDE là hình chữ nhật
=>AB=ED
=>AB=10(m)
Xét ΔABE vuông tại A có \(tanABE=\dfrac{AE}{AB}\)
=>\(\dfrac{AE}{10}=tan10\)
=>\(AE=10\cdot tan10\simeq1,76\left(m\right)\)
Xét ΔBAC vuông tại A có \(tanABC=\dfrac{AC}{AB}\)
=>\(AC=10\cdot tan55\simeq14,28\left(m\right)\)
Chiều cao của tháp là:
14,28+1,76=16,04(m)