Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: góc AEH+góc AFH=180 độ
=>AEHF nội tiếp
b: góc DFC=góc EBC
góc EFC=góc DAC
góc EBC=góc DAC
=>góc DFC=góc EFC

a) Do BE và CF là các đường cao trong tam giác ABC nên ˆBEC=90∘, ˆBFC=90∘
Tứ giác BCEF có góc E và góc F cùng nhìn cạnh BC và bằng nhau (cùng bằng 90∘) nên là tứ giác nội tiếp.
b) Tứ giác BCEF là tứ giác nội tiếp nên ˆAFE=ˆACB, mà ˆACB=ˆASB (cùng chắn cung AB) nên ˆAFE=ˆASB
Suy ra tứ giác BFMS là tứ giác nội tiếp.
Do đó ˆFMS=180∘−ˆFBS=90∘.. Vậy OA ⊥⊥ EF.
c)
+) Tứ giác BCEF nội tiếp nên ˆAEF=ˆABC (1)
Từ OA ⊥ PE suy ra ˆAIB=ˆAPE(cùng phụ với ˆMAP). (2)
Từ (1) và (2) suy ra ΔAPE∽ΔABI (g.g).
+) Tứ giác BHCS có BH // CS (cùng vuông góc với AS) và BS // CH (cùng vuông góc với AB) nên là hình bình hành. Do đó ba điểm H, K, S thẳng hàng.
Ta sẽ chứng minh hai góc đồng vị ˆPIM và HSM^ bằng nhau.
Tứ giác PDIM nội tiếp (vì có hai góc vuông M và D đối nhau) nên ˆPIM=ˆPDM (3)
Ta có:
ΔAHE∽ΔACDΔ nên AH.AD = AE.AC.
ΔAME∽ΔACSnên AM.AS = AE.AC.
Suy ra AH.AD = AM.AS ⇒AH/AM=AS/AD.
Do đó ΔMAH∽ΔDAS(c.g.c). Suy ra AHM^=ASD^.
Từ đó ta có tứ giác DHMS là tứ giác nội tiếp. Suy ra ˆHDM=ˆHSM. (4)
Từ (3) và (4) suy ra HS // PI, hay KH // PI.

Gọi L' là giao của AD với BK
=>BL'//AC
=>BL;/AC=DB/DC
BL=BL'
BL=BK
=>BK=BL'
=>BK/AC=BK'/AC=DB/DC
mà BK/AC=SB/SC
nên cần chứng minh SB/SC=DB/DC
DB/DC*FC/FA*EA/EB=1
SB/SC*FC/FA*EA/EB=1
=>DB/DC=SB/SC
=>A,D,L thẳng hàng

\({}\)
a) Vì \(\widehat{BEC}=\widehat{BFC}=90^o\) nên tứ giác BEFC nội tiếp đường tròn đường kính BC. Tương tự như thế, tứ giác AEDB nội tiếp đường tròn đường kính AB. Cũng có \(\widehat{AEH}=\widehat{AFH}=90^o\) nên tứ giác AEHF nội tiếp đường tròn đường kính AH.
Ta có \(\widehat{IEM}=\widehat{IEB}+\widehat{BEM}\)
\(=\left(90^o-\widehat{IEA}\right)+\widehat{EBC}\)
\(=90^o-\widehat{EAD}+\widehat{EBD}=90^o\) (do \(\widehat{EBD}=\widehat{EAD}\))
Vậy \(IE\perp ME\)
b) Dễ thấy các điểm I, D, E, F, M, K cùng thuộc đường tròn đường kính IM. Gọi J là trung điểm AI thì I chính là tâm của đường tròn (AIK) nên (J) tiếp xúc với (I) tại A. Dẫn đến A nằm trên trục đẳng phương của (I) và (J)
Mặt khác, ta có \(SK.SI=SE.SF\) nên \(P_{S/\left(I\right)}=P_{S/\left(J\right)}\) hay S nằm trên trục đẳng phương của (I) và (J). Suy ra AS là trục đẳng phương của (I) và (J). \(\Rightarrow\)\(AS\perp IJ\) hay AS//BC (đpcm).
c) Ta thấy tứ giác AKEP nội tiếp đường tròn AP
\(\Rightarrow\widehat{APB}=\widehat{MKE}=\widehat{MDE}=\widehat{BAC}\)
\(\Rightarrow\Delta BAE~\Delta BPA\left(g.g\right)\Rightarrow\widehat{BAP}=\widehat{BEA}=90^o\)
\(\Rightarrow\) AP//QH \(\left(\perp AB\right)\)
\(\Rightarrow\widehat{IAP}=\widehat{IHQ}\) (2 góc so le trong)
Từ đó dễ dàng chứng minh \(\Delta IAP=\Delta IHQ\left(g.c.g\right)\) \(\Rightarrow IP=IQ\) hay I là trung điểm PQ (đpcm)

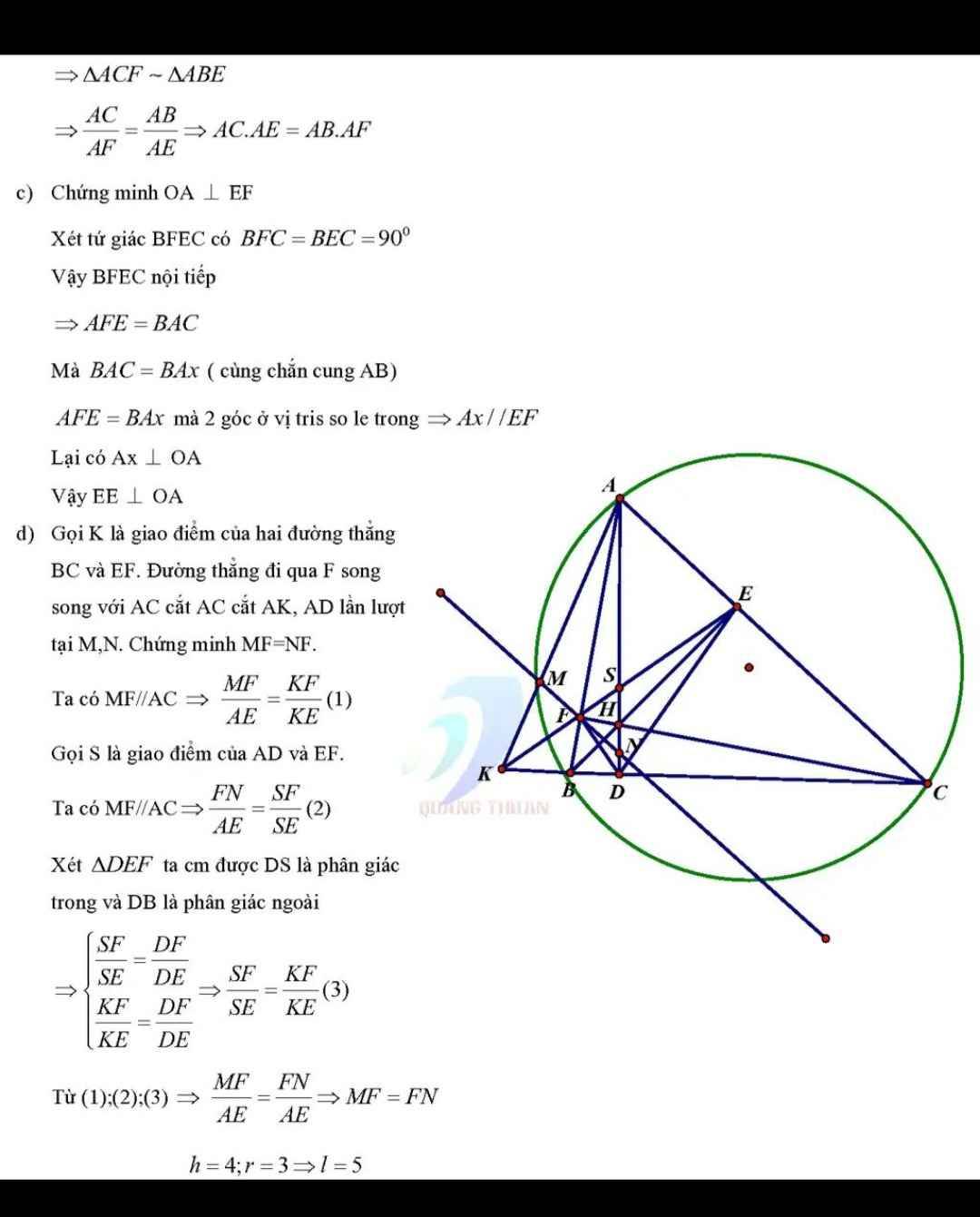
Gọi G là giao điểm của FC và AK.
Áp dụng định lý Menelaus cho tam giác FBC với cát tuyến A, G, K ta có:
\(\dfrac{AF}{AB}.\dfrac{KB}{KC}.\dfrac{GC}{GF}=1\Rightarrow\dfrac{GC}{GF}=\dfrac{KC}{KB}.\dfrac{AB}{AF}\). (1)
Áp dụng định lý Menelaus cho tam giác ACB với cát tuyến K, E, F ta có:
\(\dfrac{EA}{EC}.\dfrac{KC}{KB}.\dfrac{FB}{FA}=1\Rightarrow\dfrac{KC}{KB}=\dfrac{FA}{FB}.\dfrac{EC}{EA}\). (2)
Từ (1), (2) có \(\dfrac{GC}{GF}=\dfrac{EC}{EA}.\dfrac{AB}{FB}\). (*)
Mặt khác áp dụng định lý Menelaus cho tam giác AFC với cát tuyến B, H, E ta có:
\(\dfrac{HC}{HF}.\dfrac{BF}{BA}.\dfrac{EA}{EC}=1\Rightarrow\dfrac{HC}{HF}=\dfrac{AB}{FB}.\dfrac{EC}{EA}\). (**)
Từ (*), (**) ta có \(\dfrac{GC}{GF}=\dfrac{HC}{HF}\Rightarrow\dfrac{AC}{MF}=\dfrac{AC}{NF}\Rightarrow FM=FN\).

HUY ƠI T ĐANG NGỦ VỚI MẸ MÀY NÈ
Dựa trên các tính chất hình học và các định lý liên quan đến các đường thẳng, giao điểm, và các điểm đồng quy, ta có thể chứng minh rằng ba điểm A,H,DA, H, DA,H,D là thẳng hàng.