Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
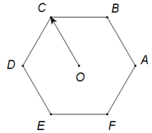
Các vecto cùng phương với ![]() có điểm đầu và điểm cuối là các đỉnh của lục giác :
có điểm đầu và điểm cuối là các đỉnh của lục giác : ![]()

Tổng số cạnh và đường chéo của đa giác n cạnh là n(n-1)/2, suy ra số đường chéo của đa giác là
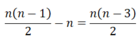
Vì mỗi đường chéo xác định hai vectơ, nên tổng số vectơ là n(n – 3)
Đáp án D

a: \(\overrightarrow{CA}+\overrightarrow{AB}+\overrightarrow{BC}\)
\(=\overrightarrow{CB}+\overrightarrow{BC}\)
\(=\overrightarrow{0}\)
b: \(\overrightarrow{AM}+\overrightarrow{AP}=\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)=\dfrac{1}{2}\cdot2\cdot\overrightarrow{AN}=\overrightarrow{AN}\)

\(\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{IA}\)
\(=\overrightarrow{IB}+2\cdot\overrightarrow{IM}\)
\(=\overrightarrow{IM}\)

MA+MC= MA-MB
<=> 2 MI=BA
=> MI=BA/2
=> I thuộc đường tròn I bán kính AB/2
nãy mk quên giải thik:
a, gọi I la trung điểm của AC=> MA+MC=2MI
hok tốt
Có tất cả \(A^2_{30}=870\) véc-tơ thỏa mãn yêu cầu bài toán (chọn ra 2 đỉnh trong 30 đỉnh sau đó chọn ra 1 điểm gốc và 1 điểm cuối)