Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hiệu 2 số là
4*2+2= 10
số bé là
[612-10]:2=301
số lớn là
612-300=311

Câu a:
Giải:
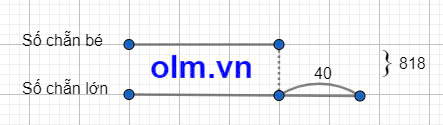
Hiệu hai số là: 2 x (20 - 1) + 2 = 40
Theo bài ra ta có sơ đồ:
Theo sơ đồ ta có:
Số chẵn bé là: (818 - 40) : 2 = 389
389 là số lẻ không thỏa mãn
Vậy không có số lẻ nào thỏa mãn đề bài

Hiệu của hai số là:
2 x 3 = 6
Số lớn là:
( 112 + 6 ) : 2 = 59
Số bé là:
112 - 59 = 53
Đ/S: 59,53
Hiệu 2 số là :
2 x 2 = 4
Số bé là :
(112 - 4) : 2 = 104
Số lớn là :
104 + 4 = 108
Đ/s : SB : 104
SL : 108
Mik hứa sẽ tk lại !

Bài giải
hiệu của hai số là: 3*2=6
số bé là: (20654-6)/2-1=10323
số lớn là: 20654-10323=10331
đáp số : số lớn 10031
số bé 10323
Bài giải
Hiệu của hai số là:
3 x 2 = 6
Số bé là:
(20654 - 6) : 2 - 1 = 10323
Số lớn là:
20654 - 10323 = 10331
Đáp số: Số lớn: 10031
Số bé: 10323

hiệu là :
4x2=8
Số lớn là :
(24778 + 8 ) : 2 =12393
số bé là :
(24778 - 8 ) : 2 =12385
tick nha
Hiệu cùa chúng là : 4x2=8 Số lớn là : (24778+8)/2=12393 Số bé là : (24778-8)/2=12385

giữa chúng có 4 số lẻ nên hiệu của chúng là 10 đơn vị. Số bé là (1992-10)2=991. Số lớn là 1992-991=1001

Hiệu 2 số đó là:
7x2=14
Số lẻ bé là:
(884-14):2=435
Số lẻ lớn là:
884-435=449
Để giải bài toán này, ta gọi hai số lẻ cần tìm là aa và bb, trong đó a<ba < b. Giữa aa và bb có 4 số lẻ nữa, do đó ta có thể biểu diễn bb theo aa như sau:
b=a+10b = a + 10Vì tổng của hai số này là 700, ta có phương trình:
a+(a+10)=700a + (a + 10) = 700Giải phương trình trên:
2a+10=7002a + 10 = 700 2a=700−102a = 700 - 10 2a=6902a = 690 a=345a = 345Do đó, bb sẽ là:
b=a+10=345+10=355b = a + 10 = 345 + 10 = 355Vậy hai số lẻ cần tìm là 345 và 355. 🌟
Nhớ tích nha