Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

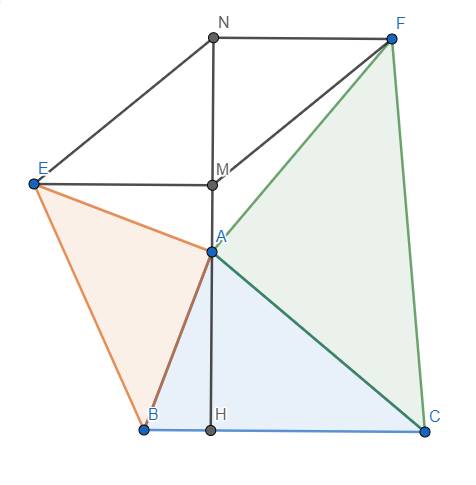
a) Do tam giác AEB vuông cân tại A nên \(\left\{{}\begin{matrix}\widehat{EAB}=90^o\\AE=AB\end{matrix}\right.\)
Ta thấy \(\widehat{MEA}=\widehat{BAH}\) vì chúng cùng phụ với \(\widehat{EAM}\)
Xét 2 tam giác HAB vuông tại H và MEA vuông tại M, ta có:
\(AE=AB\left(cmt\right),\widehat{MEA}=\widehat{BAH}\left(cmt\right)\)
\(\Rightarrow\Delta HAB=\Delta MEA\left(ch-gn\right)\) \(\Rightarrow AH=ME\) (1)
Tương tự, ta cũng có \(\Delta HAC=\Delta NFA\Rightarrow HC=AN\) (2)
Từ (1) và (2) suy ra \(EM+HC=AH+AN\) hay \(EM+HC=HN\) (đpcm)
b) Từ \(\Delta HAC=\Delta NFA\Rightarrow AH=NF\)
Từ đó suy ra \(ME=NF\left(=AH\right)\)
Xét tam giác MNE và NMF, ta có:
\(ME=NF\left(cmt\right),\widehat{EMN}=\widehat{FNM}\left(=90^o\right)\), MN là cạnh chung.
\(\Rightarrow\Delta MNE=\Delta NMF\left(c.g.c\right)\)
\(\Rightarrow\widehat{ENM}=\widehat{FMN}\) \(\Rightarrow\) EN//FM (2 góc so le trong bằng nhau)
Ta có đpcm.

a) Xét ∆AHB,∆EMA có :
^AHB = ^EMA = 90o
AB = AE (gt)
Do đó : ∆AHB = ∆EMA (ch-gn)
b) ∆AHB = ∆EMA (ch-gn)
=> EM = AH (1)
Cmtt ta cũng có : ∆AHC = ∆FNA (Ch-Gn)
=> HC = NA (2)
Từ (1)(2) => EM + HC = AH + NA
=> EM + HC = NH (A nằm giữa H,N)
d) Có : EM _|_ AH
FN _|_ AH
=> EM // FN

Bài 1
\(3A=1.2.3+2.3.3+3.4.3+...+n\left(n+1\right)=\)
\(=1.2.3+2.3.\left(4-1\right)+3.4.\left(5-2\right)+...+n.\left(n+1\right)\left[\left(n+2\right)-\left(n-1\right)\right]=\)
\(=1.2.3-1.2.3+2.3.4-2.3.4+3.4.5-...-\left(n-1\right).n.\left(n+1\right)+n\left(n+1\right)\left(n+2\right)=\)
\(=n\left(n+1\right)\left(n+2\right)\Rightarrow A=\dfrac{n\left(n+1\right)\left(n+2\right)}{3}\)
Bài 2
B C A E F M N H
a/
Xét tg vuông AEM có
\(\widehat{EAM}+\widehat{AEM}=90^o\)
Ta có
\(\widehat{EAM}+\widehat{BAH}=\widehat{MAH}-\widehat{BAE}=180^o-90^o=90^o\)
\(\Rightarrow\widehat{AEM}=\widehat{BAH}\)
Xét tg vuông AEM và tg vuông BAH có
\(\widehat{AEM}=\widehat{BAH}\)
AE=AB (cạnh bên tg cân)
=> tg AEM = tg BAH (Hai tg vuông có cạnh huyền và góc nhọn tương ứng bằng nhau)
\(\Rightarrow EM=AH\) (1)
Xét tg vuông ANF có
\(\widehat{FAN}+\widehat{AFN}=90^o\)
Ta có
\(\widehat{FAN}+\widehat{CAH}=\widehat{NAH}-\widehat{FAC}=180^o-90^o=90^o\)
\(\Rightarrow\widehat{AFN}=\widehat{CAH}\)
Xét tg vuông AFN và tg vuông CAH có
\(\widehat{AFN}=\widehat{CAH}\)
AF=AC (cạnh bên tg cân)
=> tg AFN = tg CAH (Hai tg vuông có cạnh huyền và góc nhọn tương ứng bằng nhau) => HC=AN (2)
Từ (1) và (2) => EM+HC=AH+AN=NH
b/
Ta có
tg AFN = tg CAH (cmt) => FN=AH
Mà EM=AH (cmt)
=> EM=FN
\(EM\perp AH\left(gt\right);FN\perp AH\left(gt\right)\) => EM//FN (cùng vuông góc với AH)
=> ENFM là hình bình hành (Tứ giác có 1 cặp cạnh đối // và = nhau là hbh)
=> EN//FM (trong hbh (2 cạnh đối // với nhau)

a.a. Ta có :
ΔAHB=ΔEMA(ch−gn)ΔAHB=ΔEMA(ch−gn)
AHBˆ=EMAˆ=(900)AHB^=EMA^=(900)
AB=AE(gt)AB=AE(gt)
ΔBAH=ΔAEMΔBAH=ΔAEM ( cùng phụ với ΔMAEΔMAE )
⇒EM=AH(1)⇒EM=AH(1)EM = AH (1)
Tương tự:
ΔAHC=ΔFNA(ch−gn)ΔAHC=ΔFNA(ch−gn)
⇒HC=NA(2)⇒HC=NA(2)
Từ (1)(1) và (2)(2) ⇒EM+HC=AH+NA=NH⇒EM+HC=AH+NA=NH
b) Từ ΔAHC=ΔFNAΔAHC=ΔFNA
⇒AH=NF(3)⇒AH=NF(3)
Từ (1)(1) và (3)(3)EM=MFEM=MF
Mặt khác : EM // NF ( cùng vuông góc với AH )
Ta suy ra : EN // FM

B C A E F H M N
Xét ∆AHB,∆EMA có :
^AHB = ^EMA = 90o
AB = AE (gt)
^BAH = ^AEM (vì cùng phụ với ^MAE)
Do đó : ∆AHB = ∆EMA (Ch - Gn)
=> EM = AH (1)
Cmtt ta cũng có : ∆AHC = ∆FNA (Ch-Gn)
=> HC = NA (2)
Từ (1)(2) => EM + HC = AH + NA
=> EM + HC = NH (A nằm giữa H,N)
b) Có : EM _|_ AH
FN _|_ AH
=> EM // FN

A B C E F M N
a) +)Xét tam giác EMA vuông tại M
=>góc MEA + góc MAE = 900(Định lí tổng 2 góc nhọn trong 1 tam giác vuông) (1)
+) Ta có: góc MAE + góc EAM + góc HAB = 1800
=> góc MAE + 900 + góc HAB = 1800
=>góc MAE + góc HAB = 1800(2)
Từ(1) và (2) => góc MEA= góc HAB (3)
+)Xét tam giác MEA và tam giác HAB có:
góc MEA = góc HAB(cm3)
AE=AB(vì tam giác ABE cân tại A)
góc EMA = góc AHB = 900
=>tam giác MEA= tam giác HAB(cạnh huyền-góc nhọn)
=> EM=AH(2 cạnh tương ứng) (4)
Tương tự chứng minh tam giác AHC= tam giác FNA(ch-gn)(6)
=>AN=HC(2 cạnh tương ứng) (5)
Từ (4) và (5) =>EM+HC=AN+AH
=>EM+HC=NH(đpcm)
b) +)Ta co: tam giác AHC=tam giác FNA (cm6)
=>AH=FN(2 cạnh tương ứng)(7)
từ (4) và (7)=>EM=FN(8)
+)Xét tam giác NEM và tam giác MFN có:
EM=FN(cm8)
góc EMN=góc FNM=900
MN là cạnh chung
=>tam giác NEM= tam giác MFN(cgc)
=>EN=FM(2 cạnh tương ứng)
Hiện nay bố mang bẩy tuổi biết tuổi con sang năm bằng phần bốn tuổi bố năm ngoái hỏi mấy năm nữa thì tổng số tuổi hai bố con bằng năm mốt tuổi
Hiện nay bố 37 tuổi biết tuổi con sang năm bằng một phần bốn tuổi bố năm ngoái hỏi mấy năm nữa thì tổng số tuổi hai bố con bằng năm mốt tuổi