Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Phương pháp:
Tính bán kính hai khối cầu dựa vào các mối quan hệ đường tròn nội tiếp tam giác.
Tính thể tích hai khối cầu đã cho theo công thức V = 4 3 π . R 3 và suy ra kết luận.
Cách giải: Cắt món đồ chơi đó bằng mặt phẳng đứng đi qua trục hình nón.
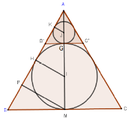
Gọi P, H, K lần lượt là hình chiếu vuông góc của M, I, J trên AB.
Vì B A C = 2 β = 60 ° , A M = 9 c m .
⇒ B M = M C = 3 3 A B = A C = 6 3 = B C ⇒ Δ A B C đều.
Vì IM là bán kính mặt cầu nội tiếp tam giác đều ABC nên I H = I M = A M 3 = 3
Gọi là tiếp tuyến chung của hai đường tròn. Vì Δ A B C đều nên dẫn đến Δ A B ' C ' đều.
Suy ra bán kính đường tròn nội tiếp:
J K = J G = A G 3 = A M 9 = 1
Vậy tổng thể tích là:
V 1 + V 2 = 4 3 π . I H 3 + 4 3 π . J K 3 = 112 π 3
Chú ý khi giải:
Cần chú ý vận dụng các mối quan hệ đường tròn nội, ngoại tiếp tam giác đều trong việc tính bán kính các khối cầu.

Chọn đáp án C
* Giả sử hàm số
![]()
![]()
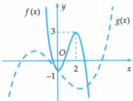
Đồ thị hàm số đi qua hai điểm 2 ; 3 , 0 ; - 1 và nhận hai điểm này làm hai điểm cực trị nên ta có hệ sau:
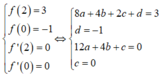
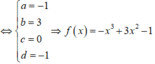
Suy ra g 0 = - f n = n 3 - 3 n 2 + 1
Mà từ đồ thị ta có g 0 = - 1
![]()
![]()
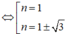
Do n ∈ ℚ nên n =1
* Hàm số g x = - f m x + n nghịch biến trên khoảng có độ dài bằng 5
⇔ Hàm số h x = - g x = f m x + n đồng biến trên khoảng có độ dài bằng 5
Quan sát đồ thị, ta thấy hàm số f x đồng biến trên khoảng 0 ; 2 nên hàm số h x = g m x + n
đồng biến trên khoảng
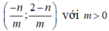
Yêu cầu bài toán
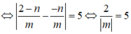
![]()
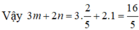

Đáp án C
Yêu cầu bài toán ⇔ 4 m + 2 log 4 2 ∈ 0 ; 2 ⇔ 2 m + 4 log 4 2 < 1 ⇔ m < 0

Câu 1.
Muốn nhân hai phân số, ta nhân các tử với nhau và nhân các mẫu với nhau. (1 điểm)
Ví dụ:
![]()
0,5 điểm
b) Muốn chia một phân số hay một số nguyên cho một phân số, ta nhân số bị chia với số nghịch đảo của số chia (1 điểm)
Ví dụ:
![]()
0,5 điểm
Câu 2. ( 2 điểm)
Tia phân giác của một góc là tia nằm giữa hai cạnh của góc và tạo với hai cạnh ấy hai góc bằng nhau (1 điểm)

Câu 3. ( 2 điểm) mỗi ý đúng 0,5 điểm
![]()
![]()
![]()

Câu 4.

0,5 điểm
Câu 5. ( 1 điểm)
Số học sinh nữ lớp 6A là: 20 . 3/10 = 6 (HS) (0,5 điểm)
Số học sinh nam lớp 6A là: 20 – 6 = 14 (HS) (0,5 điểm)
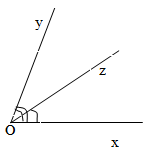
Câu 6. ( 1,5 điểm)
a) Vì ∠ xOz < ∠ xOy ( 350 <700) nên
tia Oz nằm giữa 2 tia Ox và Oy.
b) Vì tia Oz nằm giữa hai tia Ox và Oy nên
∠xOz + ∠zOy= ∠xOy hay 350 + ∠zOy = 700
=> ∠yOz = 350
c) Vì tia Oz nằm giữa hai tia Ox và Oy
và ∠xOz = ∠yOz = 350
nên Oz là tia phân giác của góc xOy

-gọi x là lượng cỏ mà 1 con bò ăn trong 1 tuần
- gọi y là lượng cỏ mọc lại trên 1arce/1 tuần
Ta có
- 12 con bò ăn trong 4 tuần: 12*4*x = 10/3 + 10/3*4y
- 21 con bò ăn trong 9 tuần: 21*9*x = 10 + 10*9*y
Giải hệ hai phương trình trên ta được: x=10/108 và y=1/12
Vậy a con bò ăn trong 18 tuần: a*18*x = 24 + 24*18*y
thay x, y vào ta tính được a=36

Gọi số trẻ trong dàn hợp xướng là n và số bạn nam là x. Theo đầu bài ta có: < x < (I) Ta nhận xét thấy rằng nếu n lẻ thì giá trị có phần thập phân là 0,5, còn nếu n chẵn thì có giá trị là một số nguyên. Nói cách khác khoảng cách từ đến giá trị nguyên lớn nhất nhỏ hơn nó là là 0,5 nếu n lẻ và là 1 nếu n chẵn. Để thoả mãn điều kiện (I), thì nếu n lẻ thì: - = >0,5 n > 5 => Giá trị lẻ nhỏ nhất của n là 7. Tương tự nếu n chẵn thì ta có: - = >1 n > 10 => Giá trị chẵn nhỏ nhất của n là 12. Nói tóm lại, 7 là giá trị nhỏ nhất mà n có thể nhận. Và thực tế nếu số trẻ của dàn hợp xướng là 7 trong đó số nam là 3 sẽ thoả mãn điều kiện (I). Thực vậy: x 7 = < = 3 = x 6 < x 7 Trả lời : Số trẻ em tham gia dàn hợp xướng nhỏ nhất có thể là 7.tick nha!![]()
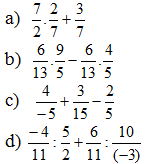
Bạn ơi , bạn bổ sung đề nhé!