Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tự vẽ hình nhá
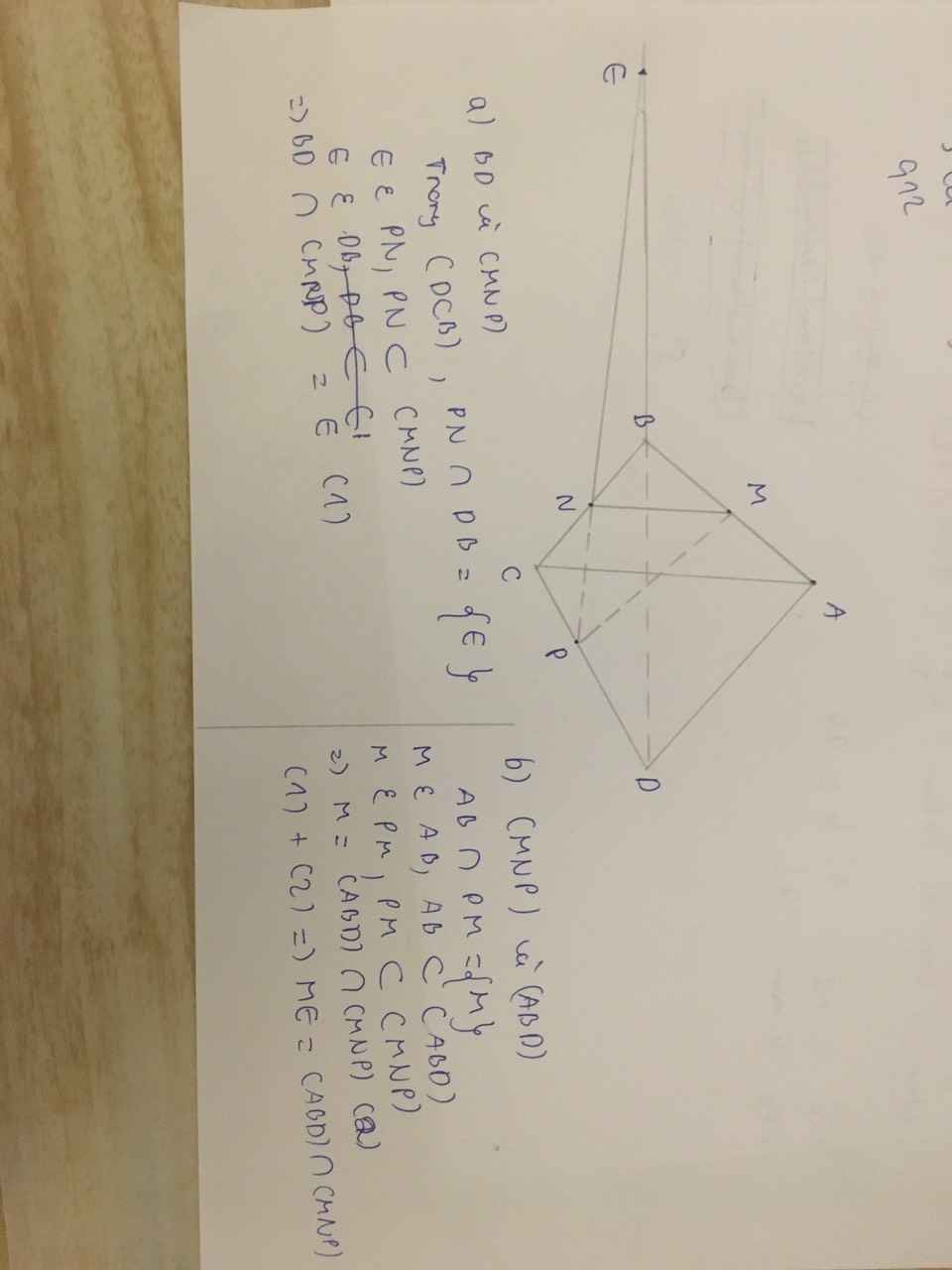
a, \(P\subset BD\in\left(ABD\right)\)
=> P là điểm chung của \(\left(MNP\right)vs\left(ABD\right)\)
Trong tam giác ABC có :
N là trung điểm AC
M là trung diểm BC
=> MN là đường trung bình của tg ABC => MN song song AB
Qua P kẻ (d) song song với AB
vậy giao tuyến 2mp là (d)
b, Vì QD=2QA => A là trung điểm QD
tương tự thì B là trung điểm DP
\(Q\subset AD\in ADB\)
\(P\subset DB\in ABD\)
trong tam giacs AQP có
A là trung điểm DP
B là trung điểm DP
=>AB là đường trung bình tg AQP
=> AB song song QP. mà \(AB\in ABC\)
=> QP song song (ABC)

Tham khảo:

a) Xét trên mp(BCD): NP cắt CD tại I
I thuộc NP suy ra I nằm trên mp(MNP)
Suy ra giao điểm của CD và mp(MNP) là I
b) Ta có I, M đều thuộc mp(ACD) suy ra IM nằm trên mp(ACD)
I, M đều thuộc mp(MNP) suy ra IM nằm trên mp(MNP)
Do đó, IM là giao tuyến của 2 mp(ACD) và mp(MNP) hay EM là giao tuyến của 2 mp(ACD) và mp(MNP).

a) Ta có: MP cắt BC tại E mà BC thuộc (BCD)
Nên: E là giao điểm của đường thẳng MP với mặt phẳng (BCD).
b) Ta có: EN cắt CD tại Q mà EN thuộc (MNP)
Nên: Q là giao điểm của đường thẳng CD với mặt phẳng (MNP).
c) Ta có: P thuộc (MNP) và (ACD)
Q thuộc (MNP) và (ACD)
Nên PQ là giao tuyến của mặt phẳng (ACD) với mặt phẳng (MNP).
d) △ACN có: \(\dfrac{AP}{AC}=\dfrac{AG}{AN}=\dfrac{2}{3}\)
Suy ra: PG // CN
Do đó: △PIG đồng dạng với △NIC
Do đó: C, I, G thẳng hàng.

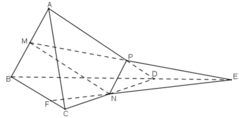
a) Trong mp(ABD): MP không song song với BD nên MP ∩ BD = E.
E ∈ MP ⇒ E ∈ (PMN)
E ∈ BD ⇒ E ∈ (BCD)
⇒ E ∈ (PMN) ∩ (BCD)
Dễ dàng nhận thấy N ∈ (PMN) ∩ (BCD)
⇒ EN = (PMN) ∩ (BCD)
b) Trong mp(BCD) : gọi giao điểm EN và BC là F.
F ∈ EN, mà EN ⊂ (PMN) ⇒ F ∈ (PMN)
⇒ F = (PMN) ∩ BC.

a) Ta có mặt phẳng (AA', DD') song song với mặt phẳng (BB',CC'). Mặt phẳng (MNP) cắt hai mặt phẳng nói trên theo hai giao tuyến song song.


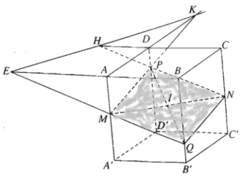
a) Ta có mặt phẳng (AA', DD') song song với mặt phẳng (BB', CC'). Mặt phẳng (MNP) cắt hai mặt phẳng nói trên theo hai giao tuyến song song.
Nếu gọi Q là điểm trên cạnh BB' sao cho NQ // PM thì Q là giao điểm của đường thẳng BB' với mặt phẳng (MNP)
Nhận xét. Ta có thể tìm điểm Q bằng cách nối P với trung điểm I của đoạn MN và đường thẳng PI cắt BB' tại Q.
b) Vì mặt phẳng (AA', BB') song song với mặt phẳng (DD', CC') nên ta có MQ // PN. Do đó mặt phẳng (MNP) cắt hình hộp theo thiết diện MNPQ là một ình bình hành.
Giả sử P không phải là trung điểm của đoạn DD'. Gọi H = PN ∩ DC , K = MP ∩ AD. Ta có D = HK là giao tuyến của mặt phẳng (MNP) với mặt phẳng (ABCD) của hình hộp.
Chú ý rằng giao điểm E = AB ∩ MQ cũng nằm trên giao tuyến d nói trên. Khi P là trung điểm của DD' mặt phẳng (MNP) song song với mặt phẳng (ABCD).

A B C D N M P K I
a) Gọi \(NP\cap CD=K\).
Do \(K\in NP\) nên \(K\in\left(MNP\right)\). Vậy K là giao điểm của CD và (MNP).
b) Do \(M\in AC\) nên \(M\in\left(MNP\right)\cap\left(ACD\right)\).
Và K là giao điểm của CD và (MNP) nên \(K\in\left(MNP\right)\cap\left(ACD\right)\).
Vì vậy MK là giao tuyến của (MNP) và (ACD).
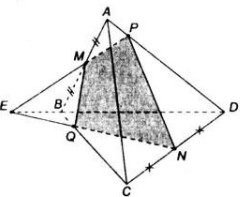
A B C D M N P Q K E
a/
Trong (ABD) Từ P dựng đường thẳng //AB cắt AD tại Q'
Xét tg ABC có
NA=NC; MB=MC => MN là đường trung bình của tg ABC
=> MN//AB và \(MN=\dfrac{1}{2}AB\)
=> MN//PQ' (cùng // với AB) \(\Rightarrow PQ'\in\left(MNP\right)\)
Ta có
\(N\in\left(MNP\right);N\in AC\Rightarrow N\in\left(ACD\right)\)
\(Q'\in\left(MNP\right);Q'\in AD\Rightarrow Q'\in\left(ACD\right)\)
=> NQ' là giao tuyến của (MNP) với (ACD)
b/
\(Q'\in AD;Q'\in\left(MNP\right)\left(cmt\right)\) => Q' là giao điểm của (MNP) với AD
c/
Xét tg ABD có
PQ//AB \(\Rightarrow\dfrac{DQ'}{Q'A}=\dfrac{DP}{PB}=2\Rightarrow DQ'=2Q'A\)
Mà \(DQ=2QA\) (gt)
\(Q;Q'\in AD\)
\(\Rightarrow Q\equiv Q'\)
Trong (ACD) Gọi K là giao của QN và DC; Từ N dựng đường thẳng //AD cắt DC tại E
Ta có \(\dfrac{DQ}{QA}=2\Rightarrow\dfrac{DQ}{DA}=\dfrac{2}{3}\Rightarrow DQ=\dfrac{2}{3}DA\)
Xét tg ACD
NA=NC; NE//AD => EC=ED (Trong tg đường thẳng đi qua trung điểm 1 cạnh và // với 1 cạnh thì đi qua trung điểm cạnh còn lại)
=> NE là đường trung bình của tg ACD \(\Rightarrow NE=\dfrac{1}{2}AD\)
\(\Rightarrow\dfrac{NE}{DQ}=\dfrac{\dfrac{1}{2}AD}{\dfrac{2}{3}AD}=\dfrac{3}{4}\)
Xét tg KQD có NE//AD
\(\Rightarrow\dfrac{KN}{KQ}=\dfrac{NE}{DQ}=\dfrac{3}{4}\Rightarrow KN=3NQ\) (1)
Xét tg ABD có PQ//AB
\(\Rightarrow\dfrac{PQ}{AB}=\dfrac{DQ}{DA}=\dfrac{2}{3}\Rightarrow PQ=\dfrac{2}{3}AB\)
Ta có \(MN=\dfrac{1}{2}AB\left(cmt\right)\)
\(\Rightarrow\dfrac{MN}{PQ}=\dfrac{\dfrac{1}{2}AB}{\dfrac{2}{3}AB}=\dfrac{3}{4}\)
Trong (MNP) gọi K' là giao của QN với PM
Xét tg KPQ có MN//PQ (cmt)
\(\Rightarrow\dfrac{K'N}{K'Q}=\dfrac{MN}{PQ}=\dfrac{3}{4}\Rightarrow K'N=3NQ\) (2)
Từ (1) và (2) \(\Rightarrow KN=K'N\) Mà K và K' đều thuốc QN \(\Rightarrow K'\equiv K\)
=> DC; QN; PM đồng qui