Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lập phương trình
Gọi số trang là: x {hỏi cái gì đắt cái đó làm ẩn}
gọi số trang đọc theo đọc được theo từng ngày là: a[1,2,3]
thì ta có hệ phương trình:\(\left\{\begin{matrix}a_1+5=\frac{1}{5}x\\a_2-7=\left(x-a_1\right)\\a_3=\frac{2}{5}\left[x-\left(a_1+a_2\right)\right]\\a_4=\frac{2}{3}\left[x-\left(a_1+a_2+a_3\right)\right]\end{matrix}\right.\)
Thiếu 1 pt: \(\left(a_1+a_2+a_3+a_4+41\right)=x\) {không vào sửa được-> viết ngoài hệ}
Như vậy ta có hệ 5 pt 5 ẩn => đủ để tìm x, (bạn tự làm)
đọc lại đề nhầm ngày thứ 4 đọc hết quyển truyện {tương còn để lại 41}
do vây--> a4=2/3[...]+41
Phuowfg trình bên ngoài hệ còn (a1+a2+a3+a4)=x

a) Giả sử số đo bốn góc của tứ giác lần lượt là \({u_1},{u_1}.q,{u_1}.{q^2},{u_1}.{q^3}\left( {{u_1},q > 0} \right)\).
Tổng số đo bốn góc của một tứ giác bằng \({360^ \circ }\) nên ta có phương trình:
\({u_1} + {u_1}.q + {u_1}.{q^2} + {u_1}.{q^3} = 360 \Leftrightarrow {u_1}\left( {1 + q + {q^2} + {q^3}} \right) = 360\left( 1 \right)\)
Số đo của góc lớn nhất gấp 8 lần số đo của góc nhỏ nhất nên ta có phương trình:
\(\frac{{{u_1}.{q^3}}}{{{u_1}}} = 8 \Leftrightarrow {q^3} = 8 \Leftrightarrow q = 2\left( 2 \right)\)
Thế (2) vào (1) ta có: \({u_1}\left( {1 + 2 + {2^2} + {2^3}} \right) = 360 \Leftrightarrow {u_1} = 24\)
Vậy số đo bốn góc của tứ giác đó là: \({24^ \circ };{24^ \circ }.2 = {48^ \circ };{24^ \circ }{.2^2} = {96^ \circ };{24^ \circ }{.2^3} = {192^ \circ }\).
b) Giả sử cấp số nhân đó có số hạng đầu \({u_1}\) và công bội \(q\).
Theo đề bài ta có: \(\left\{ \begin{array}{l}{u_1} = - 2\\{u_8} = 256\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{u_1} = - 2\\{u_1}.{q^7} = 256\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{u_1} = - 2\\{q^7} = - 128\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{u_1} = - 2\\q = - 2\end{array} \right.\).
Vậy ta cần viết thêm sáu số là:
\( - 2.\left( { - 2} \right) = 4;4.\left( { - 2} \right) = - 8;\left( { - 8} \right).\left( { - 2} \right) = 16;16.\left( { - 2} \right) = - 32;\left( { - 32} \right).\left( { - 2} \right) = 64;64.\left( { - 2} \right) = - 128\)
Số hạng thứ 15 của cấp số nhân là: \({u_{15}} = {u_1}.{q^{14}} = - 2.{\left( { - 2} \right)^{14}} = - 32768\).

Tham khảo:
a) 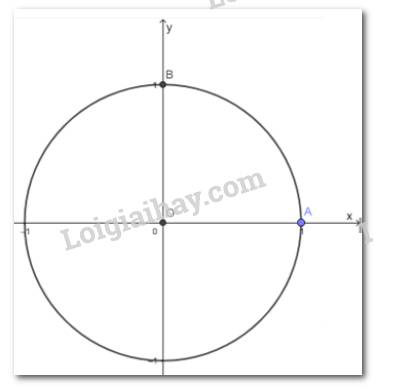
Góc lượng giác \(\left( {OA;OB} \right) = 90^\circ = \frac{\pi }{2}\)
b)
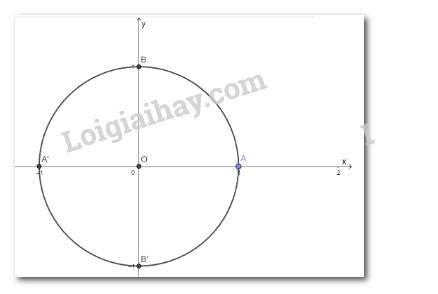

Do A, B, C, D theo thứ tự lập thành một cấp số cộng nên ta có:
B = A + d; C = A + 2d; D = A + 3d.
Mặt khác: A + B + C + D = 360°
⇔ A + A + d + A + 2d + A + 3d = 360°
⇔ 4A + 6d = 360°
⇔ 2A + 3d = 180°
Ta lại có: A + 2d = 5A ⇔ d = 2A
⇒ 8A = 180°
⇒ A = 22,5° và d = 45°
⇒ B = 67,5°, C = 112,5°, D = 157,5°.

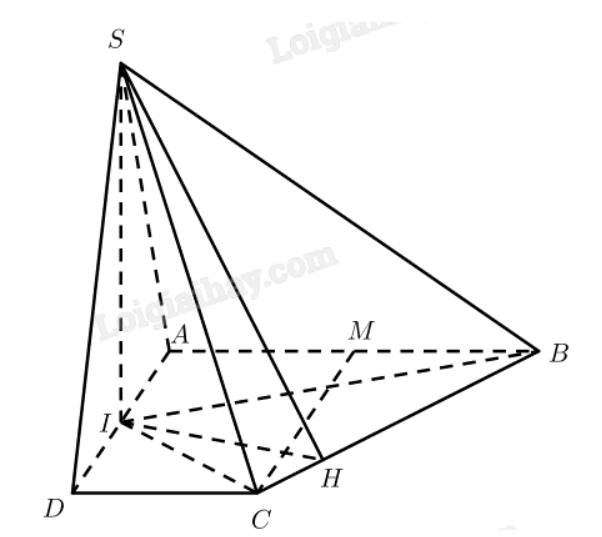
\(\left. \begin{array}{l}\left( {SBI} \right) \bot \left( {ABCD} \right)\\\left( {SCI} \right) \bot \left( {ABCD} \right)\\\left( {SBI} \right) \cap \left( {SCI} \right) = SI\end{array} \right\} \Rightarrow SI \bot \left( {ABCD} \right)\)
Kẻ \(IH \bot BC\left( {H \in BC} \right)\)
\(SI \bot \left( {ABCD} \right) \Rightarrow SI \bot BC\)
\( \Rightarrow BC \bot \left( {SIH} \right) \Rightarrow BC \bot SH\)
Vậy \(\widehat {AHI}\) là góc nhị diện \(\left[ {S,BC,A} \right]\)\( \Rightarrow \widehat {AHI} = {60^ \circ }\)
\(\begin{array}{l}{S_{ABC{\rm{D}}}} = \frac{1}{2}\left( {AB + C{\rm{D}}} \right).A{\rm{D}} = 3{a^2}\\AI = I{\rm{D}} = \frac{1}{2}A{\rm{D}} = a\\{S_{AIB}} = \frac{1}{2}AB.AI = {a^2},{S_{CI{\rm{D}}}} = \frac{1}{2}C{\rm{D}}.I{\rm{D}} = \frac{{{a^2}}}{2}\\ \Rightarrow {S_{BIC}} = {S_{ABC{\rm{D}}}} - {S_{AIB}} - {S_{CI{\rm{D}}}} = \frac{{3{a^2}}}{2}\end{array}\)
Gọi \(M\) là trung điểm của \(AB\)
\(\begin{array}{l} \Rightarrow BM = \frac{1}{2}AB = a,CM = AD = 2a \Rightarrow BC = \sqrt {B{M^2} + C{M^2}} = a\sqrt 5 \\ \Rightarrow IH = \frac{{2{{\rm{S}}_{BIC}}}}{{BC}} = \frac{{3a\sqrt 5 }}{5} \Rightarrow SI = IH.\tan \widehat {SHI} = \frac{{3a\sqrt {15} }}{5}\end{array}\)
\({V_{S.ABC{\rm{D}}}} = \frac{1}{3}{S_{ABC{\rm{D}}}}.SI = \frac{{3{a^3}\sqrt {15} }}{5}\)

Gọi M là trung điểm AB \(\Rightarrow AM=a\Rightarrow ADCM\) là hình vuông
\(\Rightarrow CM\perp AB\Rightarrow CM\perp\left(SAB\right)\)
\(\Rightarrow\widehat{CSM}\) là góc giữa SC và (SAB)
\(SM=\sqrt{SA^2+AM^2}=\sqrt{a^2+a^2}=a\sqrt{2}\)
\(tan\widehat{CSM}=\dfrac{CM}{SM}=\dfrac{a}{a\sqrt{2}}=\dfrac{\sqrt{2}}{2}\)
\(\Rightarrow\widehat{CSM}\approx35^015'\)
Gọi \(C\) là nhiệt độ đo bằng độ Celsius
\(F\) là nhiệt độ đo bằng thang đo Fahrenheit
a) Theo đề bài ta có :
\(F=2C\)
\(\Leftrightarrow\dfrac{9}{5}C+32=2C\)
\(\Leftrightarrow\dfrac{1}{5}C=32\Leftrightarrow C=160\)
b) \(F=\dfrac{1}{2}C\)
\(\Leftrightarrow\dfrac{9}{5}C+32=\dfrac{1}{2}C\)
\(\Leftrightarrow-\dfrac{13}{10}C=32\Leftrightarrow C=-24,62\)