AD
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NM
Nguyễn Minh Châu
VIP
19 tháng 8
a. Dựa vào đồ thị ta có:
Chu kì \(T = 2 s\), suy ra tần số góc \(\omega = \frac{2 \pi}{T} = \frac{2 \pi}{2} = \pi\) rad/s
Vận tốc cực đại của dao động: \(\text{v}_{m a x} = \omega A\)
\(\Rightarrow A = \frac{\text{v}_{m a x}}{\omega} = \frac{4}{\pi}\) cm
Thời điểm \(t = 0\), vật có \(\text{v} = \text{v}_{m a x}\), suy ra vật ở VTCB và \(\text{v} > 0\)
Khi đó: \(x = 0 \Rightarrow cos \varphi = 0 \Rightarrow \varphi = - \frac{\pi}{2}\)
Phương trình của vận tốc có dạng: \(\text{v} = \omega A cos \left(\right. \omega t + \varphi + \frac{\pi}{2} \left.\right)\)
\(\Rightarrow \text{v} = 4 cos \left(\right. \pi t - \frac{\pi}{2} + \frac{\pi}{2} \left.\right) = 4 cos \left(\right. \pi t \left.\right)\) (cm/s)
b. Phương trình dao động điều hòa có dạng: \(x = A cos \left(\right. \omega t + \varphi \left.\right)\)
\(\Rightarrow x = \frac{4}{\pi} cos \left(\right. \pi t - \frac{\pi}{2} \left.\right)\) (cm)
Phương trình của gia tốc có dạng: \(a = \omega^{2} A cos \left(\right. \omega t + \varphi + \pi \left.\right)\)
\(\Rightarrow a = \pi^{2} . \frac{4}{\pi} cos \left(\right. \pi t - \frac{\pi}{2} + \pi \left.\right) = 4 \pi cos \left(\right. \pi t + \frac{\pi}{2} \left.\right)\) (cm/s2)
MN
28 tháng 10 2017
khi đ1 và đ2 sáng bt thì
I = I đm = I1đm + I2đm ( 2 cái I này bạn tính ở từng đèn )
⇔ \(\dfrac{U}{R_{tđ}}\)= I đm = I1đm + I2đm
⇔\(\dfrac{U}{R_1+\dfrac{R_{đ2}.R_{đ1}}{R_{đ2}+R_{đ1}}}\) = I1đm + I2đm
thế số vô => R1
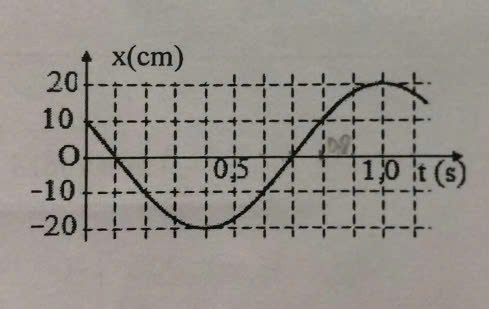
Tìm cường độ dòng điện qua các điện trở và số chỉ của ampe kế? Bỏ qua điện trở của ampe kế.
Ptrinh có dạng x=Acos(omega.t + fi)
A=20cm
T/2=0,6s => T=1,2s
omega=2pi/T=2pi/1,2=5pi/3
Tại t=0s - x=10cm
=> 10=20cos(fi)
<=>cos(fi)=1/2
<=>fi=+-pi/2
Do đồ thị chuyển động theo chiều âm nên
fi=pi/2
Vậy ptrinh đồ thị là: x=20cos(5pi/3.t + pi/2)