Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

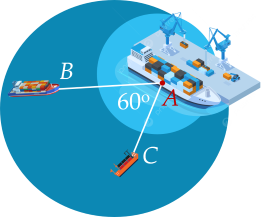
Sau 2 giờ tàu B đi được 40 hải lí, tàu C đi được 30 hải lí. Vậy tam giác ABC có AB=40,AC=30 và ˆA=600.
Áp dụng định lí côsin vào tam giác ABC, ta có
a2=b2+c2−2bccosA=302+402−2.30.40.cos600=900+1600−1200=1300
Vậy BC=√1300≈36 (hải lí).
Sau 2 giờ, hai tàu cách nhau khoảng 36 hải lí.

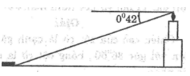
Chiều cao ngọn hải đăng là cạnh góc vuông đối diện với góc 0 ° 42 ' , khoảng cách từ tàu đến chân ngọn hải đăng là cạnh kề với góc nhọn.
Vậy khoảng cách từ tàu đến chân ngọn hải đăng là:
80.cotg 0 ° 42 ' ≈ 6547,76 (feet) ≈ 1,24 (hải lí)

Gọi vận tốc của tàu cá là x (km/h). ĐK: x > 0
Vận tốc của tàu du lịch là x + 12 (km/h)
Lúc 8 giờ tàu cá cách tọa độ X một khoảng: (8-6)x = 2x (km)
Lúc 8 giờ tàu du lịch cách tọa độ X một khoảng: (7-6)(x+12) = x+12 (km)
Vì Tàu cá đi theo hướng từ Nam đến Bắc và Tàu du lịch đi theo hướng từ Đông sang Tây và hai tàu cách nhau 60km nên ta có phương trình: (2x)2 + (x +12)2 = 602
5x2 + 24x – 3456 = 0
Giải phương trình ta được x1 = 24 (thỏa mãn) và x2 = -28,8 (loại)
Vậy vận tốc của Tàu cá là 24 km/h còn vận tốc Tàu du lịch là 36 km/h
Gọi vận tốc của tàu cá là x (km/h). ĐK: x > 0
Vận tốc của tàu du lịch là :
x + 12 (km/h)
Lúc 8 giờ tàu cá cách tọa độ X một khoảng:
(8-6)x = 2x (km)
Lúc 8 giờ tàu du lịch cách tọa độ X một khoảng:
(7-6)(x+12) = x+12 (km)
Vì Tàu cá đi theo hướng từ Nam đến Bắc và Tàu du lịch đi theo hướng từ Đông sang Tây và hai tàu cách nhau 60km nên ta có phương trình:
(2x)2 + (x +12)2 = 602
5x2 + 24x – 3456 = 0
Giải phương trình ta được x1 = 24 (thỏa mãn) và x2 = -28,8 (loại)
Vậy vận tốc của Tàu cá là 24 km/h còn vận tốc Tàu du lịch là 36 km/h

- Gọi vận tốc của tàu cá là: x (km/h), x > 0
- Vận tốc của tàu du lịch là: x + 12 km/h
- Đến 8 giờ thì hai tàu cách nhau khoảng AB = 60 km
lúc đó, thời gian tàu cá đã đi là: 8 – 6 = 2 (giờ)
thời gian tàu du lịch đã đi là: 8 – 7 = 1 (giờ)
Giả sử tàu cá đến điểm A, tàu du lịch đến điểm B
Tàu cá đã đi đoạn XA = 2x (km)
Tàu du lịch đã đi đoạn XB = = x + 12 (km)
Vì XAXB (do hai phương Bắc – Nam và Đông –Tây vuông góc nhau)
Nên theo định lý Pytago, ta có:
(loại) (nhận)
Vậy vận tốc của tàu cá và tàu du lịch lần lượt là: 24 km/h và 36 km/h
Vì Tàu cá đi theo hướng từ Nam đến Bắc và Tàu du lịch đi theo hướng từ Đông sang Tây và hai tàu cách nhau 60km nên ta có phương trình: (2x)2 + (x +12)2 = 602
5x2 + 24x – 3456 = 0
Giải phương trình ta được x1 = 24 (thỏa mãn) và x2 = -28,8 (loại)
Vậy vận tốc của Tàu cá là 24 km/h còn vận tốc Tàu du lịch là 36 km/h

Gọi vận tốc của tàu thứ nhất là \(x\left(km/h,x>0\right)\), khi đó vì vận tốc của tàu thứ nhất nhỏ hơn vận tốc của tàu thứ hai là 5km/h nên vận tốc của tàu thứ hai là \(x+5\left(km/h\right)\)
Thời gian tàu thứ nhất đi từ bến A đến bến B là \(\frac{70}{x}\left(h\right)\)
Thời gian tàu thứ hai đi từ bến A đến bến B là \(\frac{70}{x+5}\left(h\right)\)
Vì tàu thứ nhất đến chậm hơn tàu thứ hai 20 phút \(=\frac{1}{3}h\)nên ta có phương trình
\(\frac{70}{x}-\frac{70}{x+5}=\frac{1}{3}\)\(\Leftrightarrow\frac{70\left(x+5\right)-70x}{x\left(x+5\right)}=\frac{1}{3}\)\(\Leftrightarrow\frac{70x+350-70x}{x^2+5x}=\frac{1}{3}\)\(\Leftrightarrow\frac{350}{x^2+5x}=\frac{1}{3}\)\(\Rightarrow x^2+5x=1050\)\(\Leftrightarrow x^2+5x-1050=0\)\(\Leftrightarrow\)\(x^2-30x+35x-1050=0\)\(\Leftrightarrow x\left(x-30\right)+35\left(x-30\right)=0\)\(\Leftrightarrow\left(x-30\right)\left(x+35\right)=0\)\(\Leftrightarrow\orbr{\begin{cases}x-30=0\\x+35=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=30\left(TMĐK\right)\\x=-35\left(KTMĐK\right)\end{cases}}\)
Vậy vận tốc của tàu thứ nhất là 30km/h, vận tốc của tàu thứ hai là 35km/h