K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LL
27 tháng 6 2019
Noob ơi, bạn phải đưa vào máy tính ý solve cái là ra x luôn, chỉ tội là đợi hơi lâu
27 tháng 6 2019
a, 4.(18 - 5x) - 12(3x - 7) = 15(2x - 16) - 6(x + 14)
=> 72 - 20x - 36x + 84 = 30x - 240 - 6x - 84
=> (72 + 84) + (-20x - 36x) = (30x - 6x) + (-240 - 84)
=> 156 - 56x = 24x - 324
=> 24x + 56x = 324 + 156
=> 80x = 480
=> x = 480 : 80 = 6
Vậy x = 6
11 tháng 2 2022
KHÓOOOOOOOOOO QUÁAAAAAAA ĐIIIIIIIIIIIIIIIIIIII CHẾTTTTTTTTTTTTT
7 tháng 8 2017
1) 2x.(5x-3x)+2x.(3x-5)-3.(x-7)=3
10x-6x^2+6x^2-10x-3x+21=3
-3x =-18
suy ra x=6
2) 3x.(x+1) -2x.(x+2)=-1-x
3x^2 +3x-2x^2-4x =-1-x
x^2 =-1
suy ra không có giá trị nào của x thỏa mãn đề bài
3) 2x^2 +3.(x^2-1)=5x(x+1)
2x^2 +3x^2-3 =5x^2+5x
-5x =3
x=-3/5
giải rồi đấy
nhớ tích đúng nha :)
VT
3
KN
7 tháng 7 2015
1,3x+2/5x+7 =3x-1/5x+1
<=> 1,3x+2/5x-3x+1/5x = 1-7
<=> (1,3+2/5-3+1/5)x = -6
<=> -11/10x=-6
<=> x= -6 : (-11/10)
<=> x= 60/11
2.x+1/2x+1 = 0,5x+2/x +3
<=> 2x+1/2x-0,5x-2/1x = 3-1
<=> x(2+1/2-0,5-2 ) =2
<=>0x =2
<=> x=0
21 tháng 7 2016
Hinh nhu minh thay ban Kunzy Nguyen giai hoi sai
1,3x o dau ra ???????????????
VT
2
DR
12 tháng 7 2015
1) áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{3x+2}{5x+7}=\frac{3x-1}{5x+1}=\frac{\left(3x+2\right)-\left(3x-1\right)}{\left(5x+7\right)-\left(5x+1\right)}=\frac{3x+2-3x+1}{5x+7-5x-1}=\frac{3}{6}=\frac{1}{2}\)
suy ra :
\(\frac{3x-1}{5x+1}=\frac{1}{2}\Rightarrow\left(5x+1\right).1=\left(3x-1\right).2\)
=> 5x+1=6x-2
5x-6x=-2-1
-x=-3
x=3
2)áp dụng tính chất của dãy tỉ số bằng nhau ta có;
\(\frac{x+1}{2x+1}=\frac{0,5x+2}{x+3}=\frac{\left(x+1\right)-2.\left(0,5x+2\right)}{\left(2x+1\right)-2.\left(x+3\right)}=\frac{x+1-x-4}{2x+1-2x-6}=\frac{-3}{-5}=\frac{3}{5}\)
suy ra:
\(\frac{x+1}{2x+1}=\frac{3}{5}\Rightarrow\left(2x+1\right).3=\left(x+1\right).5\)
=>6x+3=5x+5
6x-5x=5-3
x=2
ND
0
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
26 tháng 3
a,(\(6x-5x^2-15+2x^3:\left(2x-5\right)\)
\(\left(2x^3-5x^2+6x-15\right):\left(2x-5\right)\)
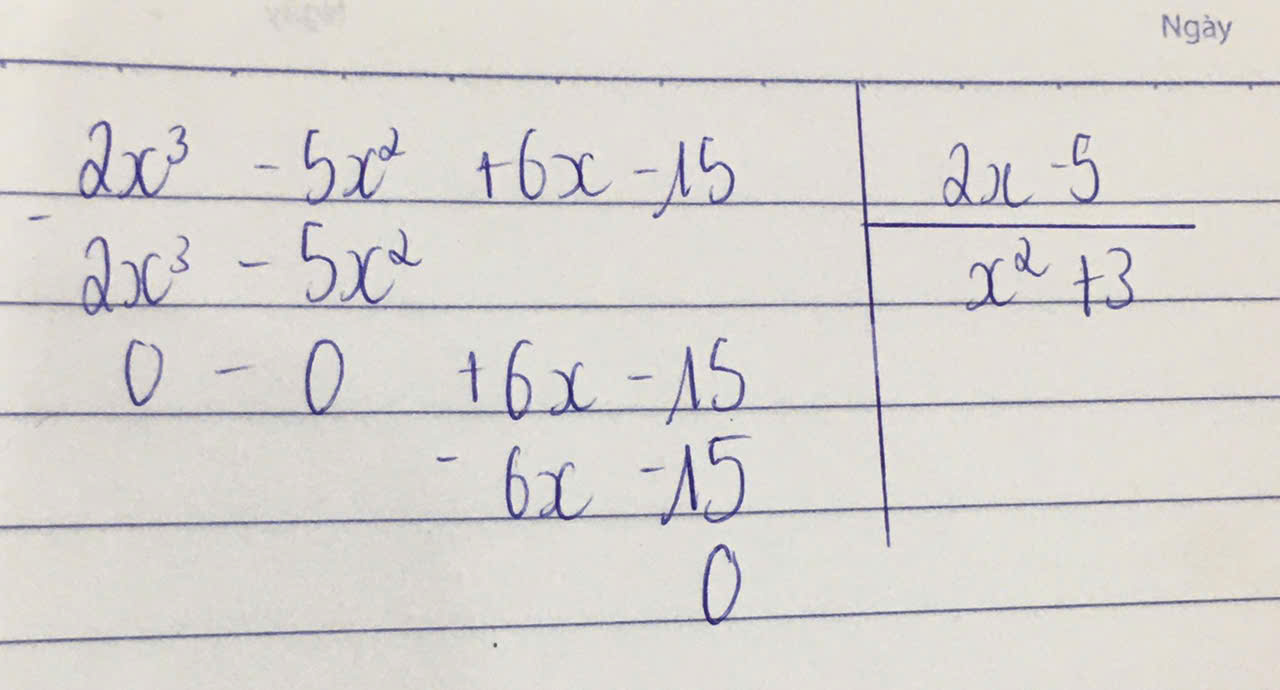
\(2\left(x-3\right)-3x=5x+1\)
\(\Rightarrow2x-6-3x=5x+1\)
\(\Rightarrow2x-3x-5x=1+6\)
\(\Rightarrow-6x=7\)
\(\Rightarrow x=7:-6\)
\(\Rightarrow x=-\dfrac{7}{6}\)
Vậy...
\(2\left(x-3\right)-3x=5x+1\)
=>\(5x+1=2x-6-3x=-x-6\)
=>\(5x+x=-6-1\)
=>6x=-7
=>\(x=-\dfrac{7}{6}\)