PB
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TT
1
2 tháng 7 2023
a Xét ΔMBD vuông tại D và ΔNCE vuông tại E có
MB=NC
góc MBD=góc NCE
=>ΔMBD=ΔNCE
b: Xét tứ giác MDNE có
MD//NE
MD=NE
=>MDNE là hình bình hành
=>MN cắt DE tại trung điểm của mỗi đường
=>I là trung điểm của DE
c: Xét ΔABO vuông tại B và ΔACO vuông tại C có
AO chung
AB=AC
=>ΔABO=ΔACO
=>OB=OC
mà AB=AC
nen AO là trung trực của BC
TN
2
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
30 tháng 9 2024
Các em đăng câu hỏi lên diễn đàn thì cần đăng đầy đủ nội dung câu hỏi lên trên này. Có như vậy mọi người mới biết yêu cầu của đề bài và trợ giúp các em tốt nhất. Cảm ơn các em đã đồng hành cùng Olm.
27 tháng 6 2019
Để phân số đó tối giản ta cần chứng minh tử và mẫu là 2 số nguyên tố cùng nhau
Đặt ( x-8; 2x-17)=d (d khác 0)
x-8 chia hết cho d
2(x-8) chia hết cho d hay 2x-16 chia hết cho d
Mặt khác 2x-17 chia hết cho d=> (2x-16)(2x-17) chia hết cho d
<=> 1 chia hết cho d => d=1
=> x-8 và 2x-17 là 2 số nguyên tố cùng nhau
=> Phân số đó tối giản với mọi giá trị của x
4 tháng 3 2022
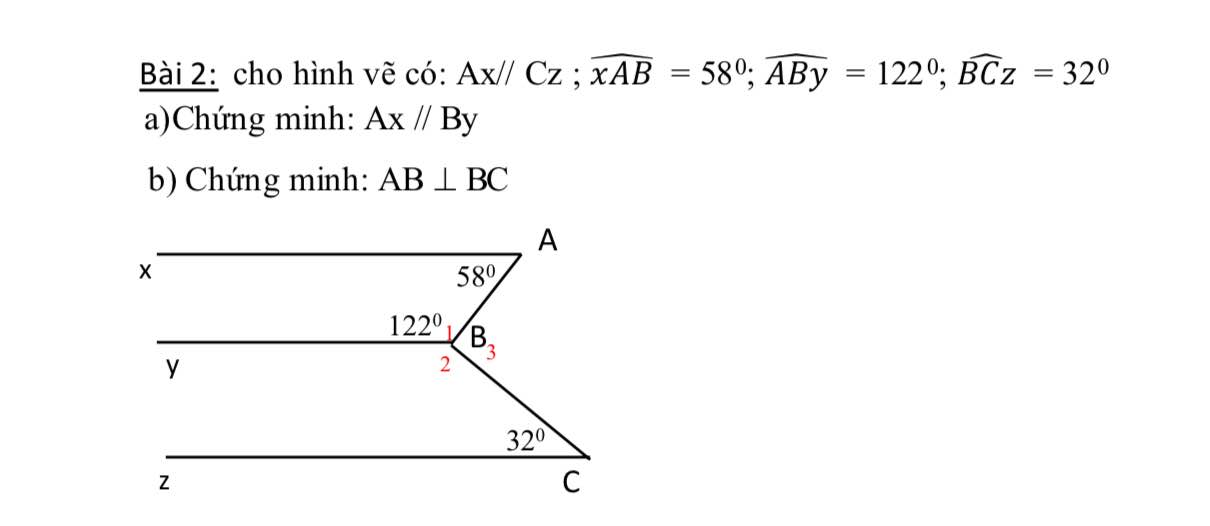
Bài 2:
a: Xét ΔAMB vuông tại M và ΔAMC vuông tại M có
AB=AC
AM chung
Do đó: ΔAMB=ΔAMC
Suy ra: MB=MC
b: Xét ΔADM vuông tại D và ΔAEM vuông tại E có
AM chung
\(\widehat{DAM}=\widehat{EAM}\)
Do đó:ΔADM=ΔAEM
Suy ra: MD=ME
hay ΔMDE cân tại M
c: Ta có: ΔADM=ΔAEM
nên AD=AE
Xét ΔABC có AD/AB=AE/AC
nên DE//BC
28 tháng 11 2017
EM MOI HOC LOP 6
KHONG BIET LAM
VA KHONG BIET TIENG ANH DAU
NEN EM XIN CHI DUNG VIET TIENG ANH
OK
BAI BAI
HEN GAP LAI KIEP SAU
13 tháng 10 2021
a) \(\Rightarrow\left(x-3\right)\left(x+4\right)=5.12\)
\(\Rightarrow x^2+x-72=0\)
\(\Rightarrow\left(x-8\right)\left(x+9\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=8\\x=-9\end{matrix}\right.\)
b) \(\Rightarrow\left(x+3\right)^2=36\)
\(\Rightarrow\left[{}\begin{matrix}x+3=6\\x+3=-6\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x=3\\x=-9\end{matrix}\right.\)
c) \(\Rightarrow2x^2=8\Rightarrow x^2=4\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\)
14 tháng 10 2021
\(a,\widehat{xAB}+\widehat{ABy}=122^0+58^0=180^0\) mà 2 góc này ở vị trí TCP nên Ax//By
\(b,\) Kẻ By' đối By
Ta có Ax//By, Ax//Cz nên By//Cz
Do đó \(\widehat{B_2}+\widehat{BCz}=180^0\left(TCP\right)\Rightarrow\widehat{B_2}=148^0\)
Ta có \(\widehat{B_1}+\widehat{B_2}+\widehat{B_3}=360^0\Rightarrow\widehat{B_3}-360^0-122^0-148^0=90^0\)
Do đó AB vuông góc BC
14 tháng 10 2021
a) Ta có: \(\widehat{xAB}+\widehat{ABy}=58^0+122^0=180^0\)
Mà 2 góc này trong cùng phía
=> Ax//By
b) Ta có: Ax//By, Ax//Cz
=> By//Cz
\(\Rightarrow\widehat{B_2}=180^0-\widehat{C}=180^0-32^0=148^0\)(trong cùng phía)
\(\Rightarrow\widehat{ABC}=360^0-\widehat{B_1}-\widehat{B_2}=360^0-122^0-148^0=90^0\)
=> AB⊥BC
23 tháng 10 2021
\(3a=2c\Leftrightarrow\dfrac{a}{2}=\dfrac{b}{3}\Leftrightarrow\dfrac{a}{10}=\dfrac{b}{15};5c=9b\Leftrightarrow\dfrac{b}{5}=\dfrac{c}{9}\Leftrightarrow\dfrac{b}{15}=\dfrac{c}{27}\\ \Leftrightarrow\dfrac{a}{10}=\dfrac{b}{15}=\dfrac{c}{27}\)
Áp dụng t/c dtsbn:
\(\dfrac{a}{10}=\dfrac{b}{15}=\dfrac{c}{27}=\dfrac{a+b-c}{10+15-27}=\dfrac{-44}{-2}=22\\ \Leftrightarrow\left\{{}\begin{matrix}a=220\\b=330\\c=594\end{matrix}\right.\)
OY
23 tháng 10 2021
Ta có: 3a=2c, 5c=9b
\(\Rightarrow\dfrac{a}{2}=\dfrac{b}{3},\dfrac{c}{9}=\dfrac{b}{5}\)
\(\Rightarrow\dfrac{a}{10}=\dfrac{b}{15}=\dfrac{c}{27}\)
Áp dụng t/c của DTSBN, ta có:
\(\dfrac{a}{10}=\dfrac{b}{15}=\dfrac{c}{27}=\dfrac{a+b-c}{10+15-27}=\dfrac{-44}{-2}=22\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{a}{10}=22\\\dfrac{b}{15}=22\\\dfrac{c}{27}=22\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=220\\b=330\\c=594\end{matrix}\right.\)
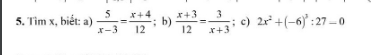
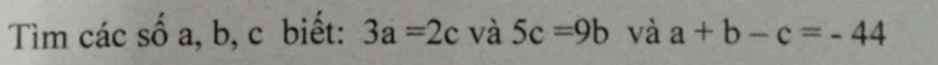
487.65