Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
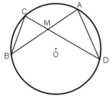
TH1: M nằm trong đường tròn.
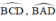là hai góc nội tiếp cùng chắn cung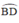 
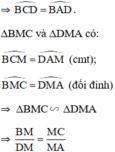
⇒ MA.MB = MC.MD
TH2: M nằm ngoài đường tròn.
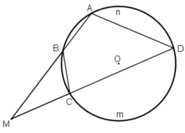
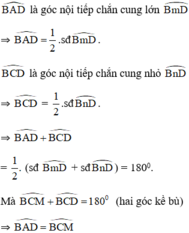
ΔMBC và ΔMDA có:
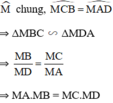
Kiến thức áp dụng
+ Góc nội tiếp chắn một cung có số đo bằng một nửa số đo của cung đó.
+ Hai góc nội tiếp chắn cùng một cung thì có số đo bằng nhau.
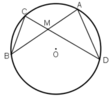
TH1: M nằm trong đường tròn.
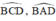là hai góc nội tiếp cùng chắn cung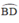 
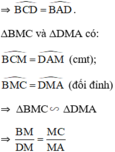
⇒ MA.MB = MC.MD
TH2: M nằm ngoài đường tròn.
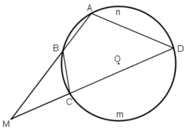
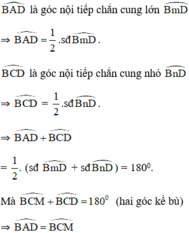
ΔMBC và ΔMDA có:
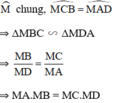
a) M ở bên trong đường tròn (hình a)
Xét hai tam giác MAB' và MA'B chúng có:
=
( đối đỉnh)
=
(hai góc nội tiếp cùng chắn cung
).
Do đó ∆MAB' ~ ∆MA'B, suy ra:
=
, do đó MA. MB = MB'. MA'
b) M ở bên ngoài đường tròn (hình b)
∆MAB' ~ ∆MA'B
M chung =
(hai góc nội tiếp cùng chắn cung
).
Suy ra: =
hay MA. MB = MB'. MA'
Xét (O) có
\(\widehat{ADC}\) là góc nội tiếp chắn cung AC
\(\widehat{ABC}\) là góc nội tiếp chắn cung AC
Do đó: \(\widehat{ADC}=\widehat{ABC}\)
=>\(\widehat{MDA}=\widehat{MBC}\)
Xét ΔMDA và ΔMBC có
\(\widehat{MDA}=\widehat{MBC}\)
\(\widehat{M}\) chung
Do đó: ΔMDA đồng dạng với ΔMBC
=>\(\dfrac{MD}{MB}=\dfrac{MA}{MC}\)
=>\(MD\cdot MC=MB\cdot MA\)
a: góc ACB=1/2*sđ cung AB=90 độ
=>ΔACN vuông cân tại C
góc ACN+góc AMN=180 độ
=>AMNC nội tiếp
b: AMNC nội tiếp
=>góc CNA=góc CMA=góc BMD
góc BNE=1/2(sđ cung BE-sđ cung AC)
góc DMB=1/2*(sđ cung BD-sđ cung AC)
=>sđ cung BD=sđ cung BE
=>B nằm trên trung trực của DE
Xét ΔADB và ΔAEB có
góc ADB=góc aEB
AB chung
DB=BE
=>ΔABD=ΔAEB
=>AD=AE
=>A nằm trên trung trực của DE
=>AB là trung trực của DE
=>DE vuông góc AB
a) MNAC nội tiếp MA.MD=MB.MC phương tích
b) ˆNCA=ˆNBA⇒NA.NB=NH.NONCA^=NBA^⇒NA.NB=NH.NO
c) ý bạn là đường thẳng nào
M A B C D
Xét tg MBC và tg MDA có
\(\widehat{BMD}\) chung
\(\widehat{MBC}=\widehat{MDA}\) (góc nội tiếp cùng chắn cung AC)
=> tg MBC đồng dạng với tg MDA (g.g.g)
\(\Rightarrow\dfrac{MA}{MC}=\dfrac{MD}{MB}\Rightarrow MA.MB=MC.MD\)