K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
1 tháng 9 2016
Chỗ khoanh bút bi thì là biến đổi tương đương từ biểu thức trước nó thôi bạn.
Còn chỗ khoanh mờ, là công thức nghiệm của hàm \(\cos x =0\)
LK
2
NB
17 giờ trước (18:57)
bn phải đứng trong top bxp GP hoặc làm bài của Đấu trường tri thức vừa mới ra ik bn
TH
Trần Hoàng Trung
VIP
17 giờ trước (18:58)
muốn kiếm GP thì cứ trả lời vào các câu hỏi giáo viên giao nếu đúng sẽ đc GP còn COIN thì rút tiền ngân hàng
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 8 2021
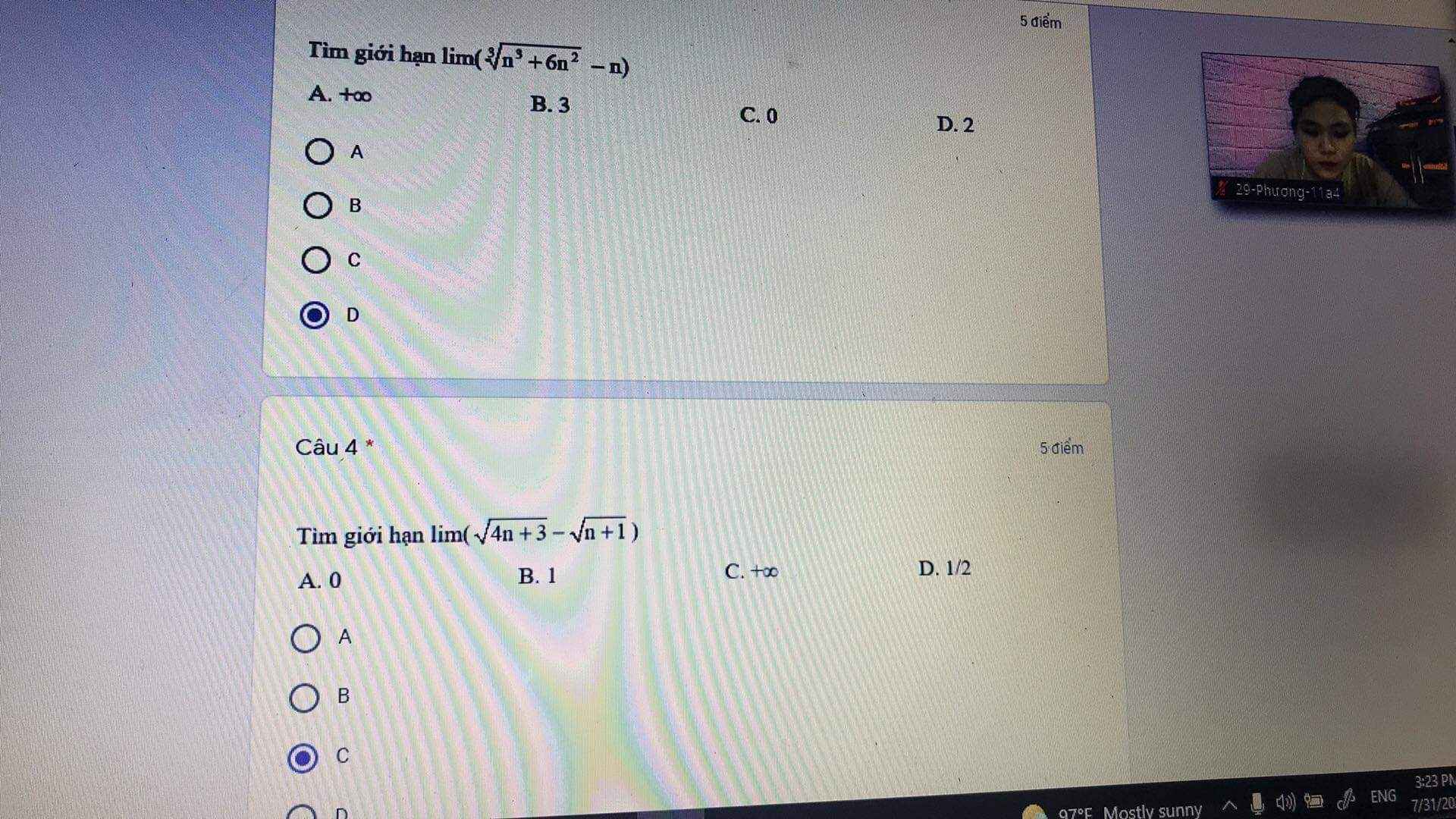
\(\lim\left(\sqrt{4n+3}-\sqrt{n-1}\right)=\lim\dfrac{3n+4}{\sqrt{4n+3}+\sqrt{n-1}}=\lim\dfrac{3+\dfrac{4}{n}}{\sqrt{\dfrac{4}{n}+\dfrac{3}{n^2}}+\sqrt{\dfrac{1}{n}-\dfrac{1}{n^2}}}=\dfrac{3}{0}=+\infty\)
MM
2
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 5 2021
Bạn nhân chéo 2 lên rồi chuyển tất cả qua vế trái là được
CM
25 tháng 7 2018
Đáp án A.
Xác suất một lần gieo được mặt một chấm là 
Xác suất để cả ba lần không gieo được mặt một chấm là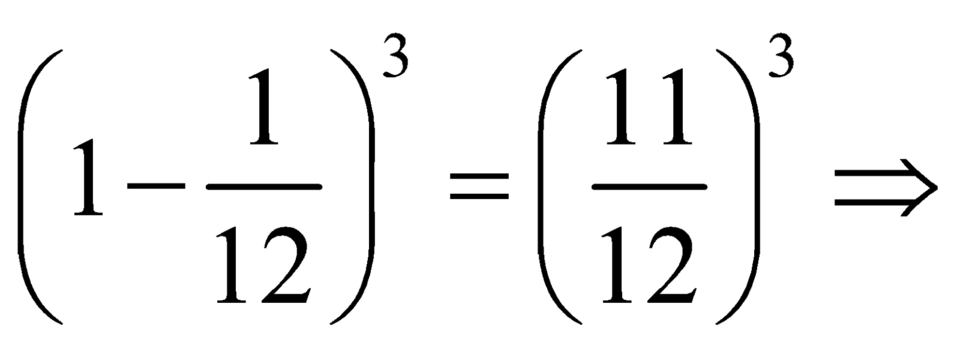 
Xác suất để có ít nhất một lần gieo được mặt một chấm trong ba lượt gieo là: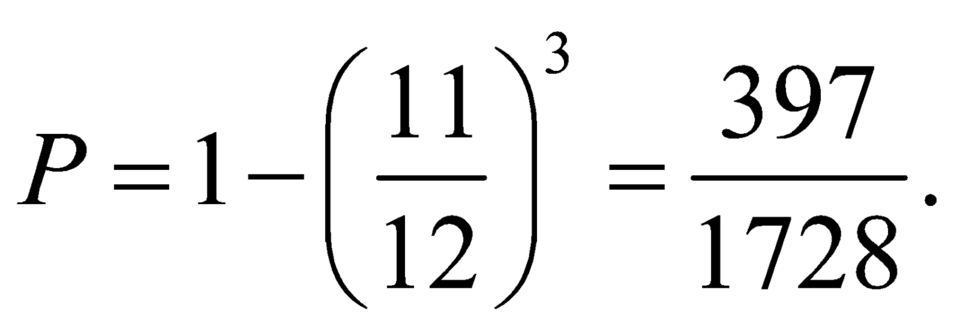 
CN
2
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
13 tháng 9
Olm chào em, để vào lớp cô Hoài em thực hiện theo hướng dẫn sau:
Bước 1 nhập mã lớp: olm-1.102018260
Bước 2: nhấn tìm kiếm
Bước 3: chọn tham gia
Bước 4 chat với cô qua Olm ghi tên mà em muốn đổi sang.
Bước 5: chờ cô duyệt và đổi tên hiển thị.
8 tháng 7 2021
Ví dụ 3:
a, - Chọn ngẫu nhiên 3 học sinh từ 35 học sinh và sắp xếp vào 3 vị trí có: \(A^3_{35}=39270\) (cách)
b, - Chọn 1 học sinh làm lớp trưởng từ 15 học sinh nam có 15 cách.
- Chọn 2 học sinh từ 34 học sinh còn lại và sắp xếp vào 2 vị trí có \(A^2_{34}\) cách.
⇒ Có: \(15.A^2_{34}=16830\) (cách)
c, - Chọn 2 học sinh từ 20 học sinh nữ và sắp xếp vào 2 vị trí lớp trưởng, lớp phó có \(A^2_{20}\) cách.
- Chọn 1 học sinh từ 33 học sinh còn lại có 33 cách.
⇒ Có: \(A^2_{20}.33=12540\) (cách)
d, - Chọn 3 học sinh từ 15 học sinh nam xếp vào 3 vị trí có \(A^3_{15}\) cách.
⇒ Có: \(A^3_{15}\) cách chọn 3 vị trí mà không có bạn nữ nào.
⇒ Có: \(39270-A^3_{15}=36540\) cách chọn 3 vị trí để có ít nhất một bạn nữ.
HP
12 tháng 9 2021
1.
\(2sinx+cosx=4\)
\(\Leftrightarrow\sqrt{5}\left(\dfrac{2}{\sqrt{5}}sinx+\dfrac{1}{\sqrt{5}}cosx\right)=4\)
\(\Leftrightarrow sin\left(x+arccos\dfrac{2}{\sqrt{5}}\right)=\dfrac{4}{\sqrt{5}}>1\)
\(\Rightarrow2sinx+4cosx-4\ne0\)
Khi đó:
\(2P.sinx+P.cosx-4P=sinx-2cosx-3\)
\(\Leftrightarrow\left(2P-1\right)sinx+\left(P+2\right)cosx=4P-3\)
Phương trình có nghiệm khi:
\(\left(2P-1\right)^2+\left(P+2\right)^2\ge\left(4P-3\right)^2\)
\(\Leftrightarrow4P^2-4P+1+P^2+4P+4\ge16P^2+9-24P\)
\(\Leftrightarrow11P^2-24P+4\le0\)
\(\Leftrightarrow\dfrac{2}{11}\le P\le2\)
\(\Rightarrow maxP=2\)
TG
1
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 8 2021
1.
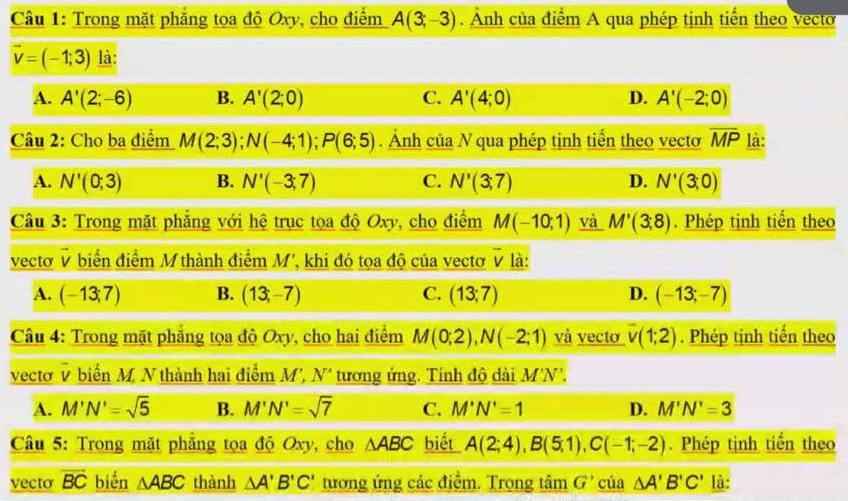
\(\left\{{}\begin{matrix}x_{A'}=x_A+\left(-1\right)=2\\y_{A'}=y_A+3=0\end{matrix}\right.\) \(\Rightarrow A'\left(2;0\right)\)
2.
\(\overrightarrow{MP}=\left(4;2\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x_{N'}=x_N+4=-4+4=0\\y_{N'}=y_N+2=1+2=3\end{matrix}\right.\)
\(\Rightarrow N'\left(0;3\right)\)
3.
\(\overrightarrow{MM'}=\left(13;7\right)\Rightarrow\overrightarrow{v}=\overrightarrow{MM'}=\left(13;7\right)\)
4.
\(\overrightarrow{MN}=\left(-2;-1\right)\Rightarrow MN=\sqrt{\left(-2\right)^2+\left(-1\right)^2}=\sqrt{5}\)
\(\Rightarrow M'N'=MN=\sqrt{5}\)
5.
Gọi G là trọng tâm ABC \(\Rightarrow G\left(2;1\right)\)
\(\overrightarrow{BC}=\left(-6;-3\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x_{G'}=2-6=-4\\y_{G'}=1-3=-2\end{matrix}\right.\) \(\Rightarrow G'\left(-4;-2\right)\)
Bn cứ lm bài theo lớp của bn. Khi bn lên hạng sẽ đc cộng xu. mà chỉ có hạng 1;2;3 mới đc cộng xu thôi nha!