
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tìm đạo hàm của hàm số \(y=\dfrac{a^3}{\sqrt{a^2-x^2}}\) (a là hằng số)
Giúp mình với ạ, mình cảm ơnn

\(y'=\dfrac{\left(a^3\right)'.\sqrt{a^2-x^2}-\left(\sqrt{a^2-x^2}\right)'.a^3}{a^2-x^2}=\dfrac{-\dfrac{1}{2\sqrt{a^2-x^2}}\left(a^2-x^2\right)'.a^3}{a^2-x^2}\)
\(y'=\dfrac{x.a^3}{\sqrt{a^2-x^2}\left(a^2-x^2\right)}\)

a) Hàm hằng ⇒ Δy = 0
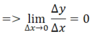
b) theo định lí 1
y = x hay y = x1 ⇒ y’= (x1)’= 1. x1-1 = 1. xo = 1.1 =1

Chọn B
y ' = 2 x . a + 2 x 2 + ( x 2 + 1 ) . 1 2 a 2 + x 2 . ( a 2 + x 2 ) ' a 2 + x 2 = 2 x . a + 2 x 2 + x ( x 2 + 1 ) a 2 + x 2 a 2 + x 2 = 2 x ( a 2 + x 2 ) + x ( x 2 + 1 ) ( a 2 + x 2 ) . a 2 + x 2 = x ( 3 x 2 + 2 a 2 + 1 ) ( a 2 + x 2 ) . a 2 + x 2
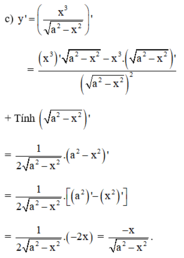
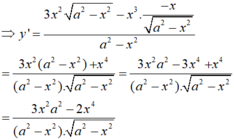
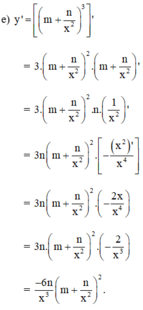

Đặt \(y=f\left(x\right)=ax^2\)
Chọn \(x=x_0\inℝ\) bất kỳ. Gọi \(\Delta x\) là số gia của biến \(x\)
Khi đó \(\Delta y=f\left(x_0+\Delta x\right)-f\left(x_0\right)\)
\(=a\left(x_0+\Delta x\right)^2-ax_0^2\)
\(=ax_0^2+2ax_0\Delta x+\left(\Delta x\right)^2-ax_0^2\)
\(=2ax_0\Delta x+\left(\Delta x\right)^2\)
Do đó \(\lim\limits_{\Delta x\rightarrow0}\dfrac{\Delta y}{\Delta x}=\lim\limits_{\Delta x\rightarrow0}\dfrac{2ax_0\Delta x+\left(\Delta x\right)^2}{\Delta x}=\lim\limits_{\Delta x\rightarrow0}\left(2ax_0+\Delta x\right)\) \(=2ax_0\)
Như vậy, \(\left(ax^2\right)'=2ax\) với a là hằng số.
Kudo Shinichi = Conan !?