Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

V1 Là vận tốc ô tô; t1 là tg v1 đi hết S=210 km
tương tự với v2;...
t' là thời gian gặp nhau
ta có: v1.t1=v2.t2=S;
v1(t'+9/4)=v2(t'+4) => t'+9/4=t1; t'+4=t2;
t'(v1+v2)=v1(t'+9/4) => v1.9/4=t'.v2; tương tự: v2.4=t'.v1
=> 9=t'^2 nên: t'=3.
=> t2=7;t'=21/4 từ đây chia là ra v1;v2.

Gọi vận tốc xe máy là x (km/h). Điều kiện: x > 0
Gọi vận tốc ô tô là y (km/h). Điều kiện: y > 0
Thời gian xe máy dự định đi từ A đến B là: 210/x giờ
Thời gian ô tô dự định đi từ B đến A là: 210/y giờ
Quãng đường xe máy đi được kể từ khi gặp ô tô cho đến khi đến B là: 4x (km)
Quãng đường ô tô đi được kể từ khi gặp xe máy cho đến khi đến A là: 9/4 (km)
Theo giả thiết ta có hệ phương trình:
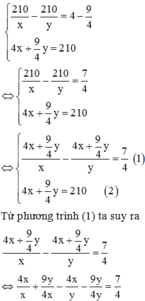

Đáp án B

chọn gốc toạ độ tại A, chiều dương là chiều chuyển động của xe máy
phương trình chuyển động của xe máy là:
\(x_1=x_{O1}+v_1\left(t-t_{O1}\right)=0+40\cdot\left(t-0\right)=40t\left(\operatorname{km};h\right)\)
phương trình chuyển động của ô tô là:
\(x_2=x_{O2}+v_2\cdot\left(t-t_2\right)=0+60\cdot\left(t-\frac12\right)=60t-30\left(\operatorname{km};h\right)\)
vì 2 xe gặp nhau cách gốc toạ độ như nhau nên ta có:
40t = 60t - 30 ⇒ 60t - 40t = 30
⇒ 20t = 30 ⇒ t = \(\frac32\left(h\right)\) = 1 giờ 30 phút
vậy ô tô đuổi kịp xe máy lúc:
8 giờ 00 phút + 1 giờ 30 phút = 9 giờ 30 phút
vị trí gặp cách A là:
40 x 1,5 = 60 (km)
vậy ô tô gặp xe máy lúc 9 giờ 30 phút và vị trí gặp cách A 60km
Trong 30 phút (từ 8h đến 8h30), xe máy đi được:
\(40\times0,5=20\text{km}.\)
→ Xe máy đi trước ô tô 20 km.
Mỗi giờ, ô tô đi nhanh hơn xe máy:
\(60-40=20\text{km}.\)
Nghĩa là cứ 1 giờ, ô tô thu hẹp được 20 km.
Vì khoảng cách ban đầu là 20 km, nên ô tô cần:
\(20:20=1\text{gi}ờ\)
Ô tô xuất phát lúc 8h30, sau 1 giờ thì gặp → lúc 9h30.Trong 1 giờ đó, ô tô đi được:
\(60\times1=60\left(\text{km}.\right)\)
đáp số:.... ( học tốt nha)

Đổi: 1h 6 phút = 1,1 giờ; 2 giờ 30 phút = 2,5 giờ
Gọi vận tốc của xe ô tô đi từ A là x ; vận tốc của xe ô tô đi từ B là y ( >0; km/h)
+) Nếu cùng khởi hành sau hai giờ chúng gặp nhau.
Sau hai giờ ô tô đi từ A đi được quãng đường là: 2x ( km)
Sau hai giờ ô tô đi từ B đi được quãng đường là: 2 y ( km)
=> Có phương trình : 2x + 2y = 220 ( km) (1)
+) Nếu xe đi từ A khởi hành trước xe đi từ B 1, 1 giờ:
Sau 2,5 h xe đi từ A đi được quãng đường là: 2,5.x ( km)
Xe đi từ B đi được quãng đường là: ( 2,5 - 1,1) .y= 1,4y (km)
=> Có phương trình: 2,5x + 1,4y - 220 (km) (2)
Từ (1) và (2) ta có hệ : \(\hept{\begin{cases}2x+2y=220\\2,5x+1,4y=220\end{cases}}\Leftrightarrow\hept{\begin{cases}x=60\\y=50\end{cases}}\) ( thỏa mãn)
Vậy...

Gọi vận tốc xe máy và ô tô là x, y
\(\hept{\begin{cases}\frac{80}{x}=\frac{100}{y}\\\frac{60}{x}=\frac{120-0,9y}{y}\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=40\\y=50\end{cases}}\)

Ta có: 1h30 = 3/2h
Gọi x(km/h) là vận tốc của xe máy ( x > 0)
Vận tốc xe ô tô là: x + 20 (km/h)
Quảng đường xe máy đi phần còn lại trong 2/3h là 2x/3 .
Vậy quảng đường xe ô tô đi từ lúc khởi hành đến lúc gặp nhau là: 2x/3 .
Quảng đường xe máy đi từ lúc khởi hành đến lúc gặp nhau là: 100-2x/3 = (200-3x)/2 .
Thời gian xe ô tô đi từ lúc khởi hành đến lúc gặp nhau là 3x/2 : (x+20) = 3x/(2x+40)
Thời gian xe máy đi từ lúc khởi hành đến lúc gặp nhau là: (200-3x)/2 : x = (200-3x)/2
Ta có pt: 3x/(2x + 40) = (200-3x)/2x
Giải pt x1=40(tm) x2 (loại)
TL: Vận tốc xe máy là: 40 km/h
Vận tốc xe ô tô là: 40 + 20 = 60 (km/h

Tổng 2 vận tốc: 390 : 6 = 65(km/h)
Nếu ô tô khởi hành trước xe máy 3h15p thì ô tô đi từ đầu đến lúc gặp xe máy:
4 giờ + 3 giờ 15 phút = 7 giờ 15 phút
Nếu ô tô khởi hành trước xe máy 3h15p thì xe máy đi được 4 giờ ít hơn đoạn khoảng thời gian 6 giờ một khoảng là 2 tiếng đồng hồ (8/4 giờ)
Nếu ô tô khởi hành trước xe máy 3h15p thì ô tô đi từ đầu đến lúc gặp xe máy nhiều hơn 6 giờ một khoảng là 1 giờ 15 phút (5/4 giờ)
Vậy quãng đường ô tô đi trong 5/4 giờ = quãng đường xe máy đi trong 2 giờ
Vậy: 5/4 x Vận tốc ô tô = 8/4 x vận tốc xe máy
Vậy vận tốc ô tô = 8/5 vận tốc xe máy
Tổng số phần bằng nhau: 5+8=13(phần)
Vận tốc xe ô tô: 65 : 13 x 8 = 40(km/h)
Vận tốc xe máy: 65 - 40 = 25 (km/h)
Đ.số:....
30 phút= 0,5 giờ
Sau 30 phút xe máy đi được: 40.0,5=20(km)
Khi đó xe máy ở điểm C trên quãng đường AB.
Độ dài quãng đường BC là: 110-20=90(km)
Vậy hai xe gặp nhau sau: \(\dfrac{90}{40+50}\)= 1(giờ)
đúng thì mình xin tick nhé