Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có :
\(\dfrac{1}{1.2}-\dfrac{1}{2.3}=\dfrac{3}{1.2.3}-\dfrac{1}{1.2.3}=\dfrac{2}{1.2.3}\)
\(\dfrac{1}{2.3}-\dfrac{1}{3.4}=\dfrac{4}{2.3.4}-\dfrac{2}{2.3.4}=\dfrac{2}{2.3.4}\)
...
Do đó :
\(\dfrac{1}{1.2.3}=\dfrac{1}{2}\left(\dfrac{1}{1.2}-\dfrac{1}{2.3}\right)\)
\(\dfrac{1}{2.3.4}=\dfrac{1}{2}\left(\dfrac{1}{2.3}-\dfrac{1}{3.4}\right)\)
Vậy :
\(M=\dfrac{1}{2}\left(\dfrac{1}{1.2}-\dfrac{1}{2.3}+\dfrac{1}{2.3}-\dfrac{1}{3.4}+\dfrac{1}{3.4}-\dfrac{1}{4.5}+...+\dfrac{1}{10.11}-\dfrac{1}{11.12}\right)\)
\(=\dfrac{1}{2}\left(\dfrac{1}{1.2}-\dfrac{1}{11.12}\right)\)
\(=\dfrac{1}{2}\left(\dfrac{1}{2}-\dfrac{1}{132}\right)\)
\(=\dfrac{1}{2}.\dfrac{65}{132}=\dfrac{65}{264}\)

\(A=\dfrac{3}{4}\cdot\dfrac{8}{9}\cdot\dfrac{15}{16}\cdot...\cdot\dfrac{899}{900}\)
\(A=\dfrac{1\cdot3}{2\cdot2}\cdot\dfrac{2\cdot4}{3\cdot3}\cdot\dfrac{3\cdot5}{4\cdot4}\cdot...\cdot\dfrac{29\cdot31}{30\cdot30}\)
\(A=\dfrac{1\cdot\left(2\cdot3\cdot4\cdot5\cdot...\cdot29\right)^2\cdot30\cdot31}{\left(2\cdot3\cdot4\cdot...\cdot30\right)^2}\)
\(A=\dfrac{1\cdot\left(2\cdot3\cdot4\cdot5\cdot...\cdot29\right)^2\cdot30\cdot31}{\left(2\cdot3\cdot4\cdot5\cdot...\cdot29\right)^2\cdot30\cdot30}\)
\(A=\dfrac{1\cdot31}{30}=\dfrac{31}{30}\)
Ta có : \(\dfrac{1}{101}>\dfrac{1}{300}\)
...
\(\dfrac{1}{299}>\dfrac{1}{300}\)
Do đó :
\(\dfrac{1}{101}+\dfrac{1}{102}+..+\dfrac{1}{300}>\dfrac{1}{300}+\dfrac{1}{300}..+\dfrac{1}{300}\)
\(\Rightarrow\dfrac{1}{101}+\dfrac{1}{102}+..+\dfrac{1}{300}>\dfrac{200}{300}=\dfrac{2}{3}\)
Vậy...

A = 1/7 +1/91 +1/247 + 1/475 + 1/775 + 1/1147
A = 1 / (1,7) + 1 / (7,13) + 1 / (13,19) + ... + 1 / (31 ...
A = (1/6) * (1 - 1/7 + 1/7 - 1/13 + ... + 1 / 31-1 / 37)
A = (1/6) * ( 1-1 / 37)
A = (1/6) * (36/37)
A = 6/37

a) Ta có:
3A= \(1+\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{99}}\left(1\right)\)
A= \(\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{100}}\left(2\right)\)
Lấy (1) - (2) ta được:
1-\(\dfrac{1}{3^{100}}\)
b) Ta xét:
\(\dfrac{1}{1.2}-\dfrac{1}{2.3}=\dfrac{2}{1.2.3},...,\dfrac{1}{37.38}-\dfrac{1}{38.39}=\dfrac{2}{37.38.39}\)
Ta có:
2B=\(\dfrac{2}{1.2.3}+\dfrac{2}{2.3.4}+..+\dfrac{2}{37.38.39}\)
=\(\left(\dfrac{1}{1.2}-\dfrac{1}{2.3}\right)+\left(\dfrac{1}{2.3}-\dfrac{1}{3.4}\right)+..+\left(\dfrac{1}{37.38}-\dfrac{1}{38.39}\right)\)
=\(\dfrac{1}{1.2}-\dfrac{1}{38.39}=\dfrac{740}{38.39}=\dfrac{370}{741}\)
Vậy \(\dfrac{2}{1.2.3}+\dfrac{2}{2.3.4}+\dfrac{2}{3.4.5}+..+\dfrac{2}{37.38.39}\)
=\(\dfrac{370}{741}\)
Nếu bn cảm thấy mk đúng tick cho mk nhé!
![]()

\(\dfrac{1}{1.2.3}+\dfrac{1}{2.3.4}+...+\dfrac{1}{10.11.12}\)
\(=\dfrac{1}{2}\left(\dfrac{2}{1.2.3}+\dfrac{2}{2.3.4}+...+\dfrac{2}{10.11.12}\right)\)
\(=\dfrac{1}{2}.\left(\dfrac{1}{1.2}-\dfrac{1}{2.3}+\dfrac{1}{2.3}-\dfrac{1}{3.4}+...+\dfrac{1}{10.11}-\dfrac{1}{11.12}\right)\)
\(=\dfrac{1}{2}.\left(\dfrac{1}{1.2}-\dfrac{1}{11.12}\right)\)
\(=\dfrac{1}{2}.\left(\dfrac{1}{2}-\dfrac{1}{132}\right)\)
\(=\dfrac{1}{2}.\dfrac{65}{132}\)
\(=\dfrac{65}{264}\)
Vậy...

hôm qua cô giảng cho mình bài này không cần tính đâu
Gọi tổng là A
A=\(\dfrac{1}{1.2.3}+\dfrac{1}{2.3.4}+...+\dfrac{1}{17.18.19}\)
2A=\(\dfrac{2}{1.2.3}+\dfrac{2}{2.3.4}+...+\dfrac{2}{17.18.19}\)
2A=\(\dfrac{1}{1.2}-\dfrac{1}{2.3}+\dfrac{1}{2.3}-\dfrac{1}{3.4}+...+\dfrac{1}{17.18}-\dfrac{1}{18.19}\)
2A=\(\dfrac{1}{2}-\dfrac{1}{18.19}\)
A=\(\dfrac{1}{2}.\left(\dfrac{1}{2}-\dfrac{1}{18.19}\right)\)
A=\(\dfrac{1}{2}.\dfrac{18.19-2}{2.18.19}\) < \(\dfrac{1}{4}\)
A=\(\dfrac{18.19-2}{2.2.18.19}\) < \(\dfrac{18.19}{2.2.18.19}\)
\(\Rightarrow\) A<\(\dfrac{1}{4}\)
\(\dfrac{1}{1.2.3}\)+\(\dfrac{1}{2.3.4}\)+\(\dfrac{1}{3.4.5}\)+...+\(\dfrac{1}{17.18.19}\)<\(\dfrac{1}{4}\)
Đặt A=\(\dfrac{1}{1.2.3}\)+\(\dfrac{1}{2.3.4}\)+\(\dfrac{1}{3.4.5}\)+...+\(\dfrac{1}{17.18.19}\)
2.A=2.(\(\dfrac{1}{1.2.3}\)+\(\dfrac{1}{2.3.4}\)+\(\dfrac{1}{3.4.5}\)+...+\(\dfrac{1}{17.18.19}\))
2. A=\(\dfrac{2}{1.2.3}\)+\(\dfrac{2}{2.3.4}\)+\(\dfrac{2}{3.4.5}\)+...+\(\dfrac{2}{17.18.19}\)
2.A=\(\dfrac{1}{1.2}\)-\(\dfrac{1}{2.3}\)+\(\dfrac{1}{2.3}\)-\(\dfrac{1}{3.4}\)+ ...+\(\dfrac{1}{17.18}\)-\(\dfrac{1}{18.19}\)
2.A=\(\dfrac{1}{1.2}\)-\(\dfrac{1}{18.19}\)=\(\dfrac{85}{171}\)
A=\(\dfrac{85}{171}\):2=\(\dfrac{85}{342}\)
Ta cũng có: \(\dfrac{1}{4}\) = \(\dfrac{171}{684}\); \(\dfrac{85}{342}\) = \(\dfrac{170}{684}\)
Vì 170 < 171 ( \(\dfrac{170}{684}\) < \(\dfrac{171}{684}\) )
Vậy \(\dfrac{1}{1.2.3}+\dfrac{1}{2.3.4}+\dfrac{1}{3.4.5}+...+\dfrac{1}{17.18.19}\) < \(\dfrac{1}{4}\)

A= \(\dfrac{1}{1.2.3}+\dfrac{1}{2.3.4}+\dfrac{1}{4.5.6}+....+\dfrac{1}{37.38.39}\)
A=\(\dfrac{1}{1}-\dfrac{1}{39}\)
A=\(\dfrac{38}{39}\)
còn lại tự làm do mình có việc chút

a, A= 1/2. (2/1.2.3+2/2.3.4+2/3.4.5+...+2/18.19.20) A=1/2. (1/1.2-1/2.3+1/2.3-1/3.4+1/3.4-1/4.5+...+1/18.19-1/19.20) A=1/2. (1/1.2-1/19.20) A=1/2. 189/380 A= 189/760

\(A=\dfrac{1}{1.2.3}+\dfrac{1}{2.3.4}+\dfrac{1}{3.4.5}+...+\dfrac{1}{18.19.20}\)
\(A=\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+...+\dfrac{1}{18.19}+\dfrac{1}{19.20}\)
\(A=\dfrac{1}{1}-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+...+\dfrac{1}{18}-\dfrac{1}{19}+\dfrac{1}{19}-\dfrac{1}{20}\)
\(A=\dfrac{1}{1}-\dfrac{1}{20}\)
\(A=\dfrac{20}{20}-\dfrac{1}{20}\)
\(A=\dfrac{19}{20}\)
A = \(\dfrac{1}{1.2.3}\)+\(\dfrac{1}{2.3.4}\)+\(\dfrac{1}{3.4.5}\)+...+\(\dfrac{1}{18.19.20}\)
A = \(\dfrac{1}{1.2}\)-\(\dfrac{1}{2.3}\)+\(\dfrac{1}{2.3}\)-\(\dfrac{1}{3.4}\)+...+\(\dfrac{1}{18.19}\)-\(\dfrac{1}{19.20}\)
A = \(\dfrac{1}{1.2}\)-\(\dfrac{1}{19.20}\)
A = \(\dfrac{1}{2}\)-\(\dfrac{1}{380}\)
A = \(\dfrac{189}{380}\)
(Mình nghĩ là vậy, có gì sai bạn bỏ qua nha ![]() )
)
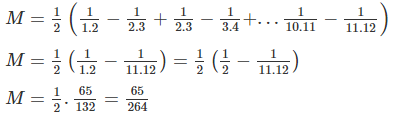
`P = 1/(1.2.3) + 1/(2.3.4) + ... + 1/(10.11.12) `
`2P = 2/(1.2.3) + 2/(2.3.4) + ... + 2/(10.11.12) `
`2P = 1/(1.2) - 1/(2.3) + 1/(2.3) - 1/(3.4) + ... + 1/(10.11) - 1/(11.12) `
`2P = 1/(1.2) - 1/(11.12) `
`2P = 1/2 - 1/132 `
`2P = 65/132`
`P = 65/264`
`Vậy ..
Câu C chắc em ghi sai đề ở số hạng gần cuối, đề là \(\dfrac{1}{775}\) mới đúng