
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 3:
a: Ta có: \(\left(1-4x\right)\left(x-1\right)+\left(2x+1\right)\left(2x+3\right)=38\)
\(\Leftrightarrow x-1-4x^2+4x+4x^2+6x+2x+3=38\)
\(\Leftrightarrow13x=36\)
hay \(x=\dfrac{36}{13}\)
b: Ta có: \(\left(2x+3\right)\left(x+2\right)-\left(x-4\right)\left(2x-1\right)=75\)
\(\Leftrightarrow2x^2+4x+3x+6-2x^2+x+8x-4=75\)
\(\Leftrightarrow15x=73\)
hay \(x=\dfrac{73}{15}\)


Có : x2 + 12 > 0 với mọi x
=> 4x - 1 > 0 , -x + 4 > 0 hoặc 4x - 1 < 0 , -x + 4 < 0
=> x > 1/4 , x < 4 hoặc x < 1/4 , x > 4
=>1/4 < x < 4 (thỏa mãn) hoặc 1/4 > x > 4(không thỏa mãn)
Vậy 1/4 < x < 4


a. Xét tam giác OHP và tam giác OPQ, có:
\(\widehat{H}=\widehat{A}=90^0\)
\(\widehat{P}:chung\)
Vậy tam giác OHP đồng dạng tam giác OPQ ( g.g )
\(\Rightarrow\dfrac{OP}{PQ}=\dfrac{PH}{OP}\)
\(\Leftrightarrow OP^2=PH.PQ\)
b.Xét tam giác OHP và tam giác OHQ, có:
\(\widehat{H}=90^0\)
\(\widehat{HQO}=\widehat{HOP}\) ( cùng phụ với góc P )
Vậy tam giác OHP đồng dạng tam giác OHQ ( g.g )
\(\Rightarrow\dfrac{OH}{PH}=\dfrac{HQ}{OH}\)
\(\Rightarrow OH^2=PH.OH\)
c.Xét tam giác OHQ và tam giác OPQ, có:
\(\widehat{H}=\widehat{A}=90^0\)
\(\widehat{Q}:chung\)
Vậy tam giác OHQ đồng dạng tam giác OPQ ( g.g )
\(\Rightarrow\dfrac{OH}{OP}=\dfrac{OQ}{PQ}\)
\(\Leftrightarrow OH.PQ=OQ.OP\)
a: Xét ΔOPQ vuông tại O có OH là đườg cao
nên \(OP^2=PH\cdot PQ\)(hệ thức lượng)
b: Xét ΔOPQ vuông tại O có OH là đường cao
nên \(OH^2=HP\cdot HQ\)(hệ thức lượng)
c: Xét ΔOPQ vuông tại O có OH là đường cao
nên \(OH\cdot PQ=OP\cdot OQ\)

a: Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
=>ADHE là hình chữ nhật
b: ΔHDB vuông tại D
mà DI là đường trung tuyến
nên IH=ID=IB
=>IH=ID
=>ΔIHD cân tại I
=>\(\widehat{IDH}=\widehat{IHD}\)
mà \(\widehat{IHD}=\widehat{BCA}\)(hai góc đồng vị, HD//AC)
nên \(\widehat{IDH}=\widehat{BCA}\)
Ta có: ADHE là hình chữ nhật
=>\(\widehat{EDH}=\widehat{EAH}=\widehat{HAC}\)
mà \(\widehat{HAC}=\widehat{ABC}\left(=90^0-\widehat{HAB}\right)\)
nên \(\widehat{EDH}=\widehat{ABC}\)
\(\widehat{EDI}=\widehat{EDH}+\widehat{IDH}\)
\(=\widehat{ABC}+\widehat{ACB}\)
\(=90^0\)
=>ED\(\perp\)DI
c: Ta có: ΔCEH vuông tại E
mà EK là đường trung tuyến
nên KE=KH
=>ΔKEH cân tại K
=>\(\widehat{KEH}=\widehat{KHE}\)
mà \(\widehat{KHE}=\widehat{ABC}\)(hai góc đồng vị, EH//AB)
nên \(\widehat{KEH}=\widehat{ABC}\)
Ta có: ADHE là hình chữ nhật
=>\(\widehat{DEH}=\widehat{DAH}\)
mà \(\widehat{DAH}=\widehat{ACB}\left(=90^0-\widehat{ABC}\right)\)
nên \(\widehat{DEH}=\widehat{ACB}\)
\(\widehat{KED}=\widehat{KEH}+\widehat{DEH}\)
\(=\widehat{ABC}+\widehat{ACB}=90^0\)
=>KE\(\perp\)ED
mà DI\(\perp\)DE
nên DI//KE
Xét tứ giác EKID có DI//EK
nên EKID là hình thang
Hình thang EKID có \(\widehat{KED}=90^0\)
nên EKID là hình thang vuông
d: DI=HB/2
=>HB=2*DI=2(cm)
EK=1/2CH
=>\(CH=2\cdot EK=2\cdot4=8\left(cm\right)\)
BC=BH+CH
=2+8
=10(cm)
Xét ΔABC có AH là đường cao
nên \(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC=\dfrac{1}{2}\cdot10\cdot6=30\left(cm^2\right)\)

Bài làm
7x2 - 42x + 63
= 7( x2 - 6x + 9 )
= 7( x - 3 )2
~ Phân tích đa thức thqành nhân tử nhỉ, tích nha.~
# Học tốt #

`c)-x^2+7x-2=-(x^2-7x)-2`
`=-(x^2-7x+49/4-49/4)-2`
`=-(x-7/2)^2+49/4-2`
`=-(x-7/2)^2+41/4<=41/4`
Dấu "=" xảy ra khi `x=7/2`
`d)-4x^2+8x-9=-(4x^2-8x)-9`
`=-(4x^2-8x+4-4)-9`
`=-(2x-2)^2-5<=-5`
Dấu "=" xảy ra khi `x=1`
`e)-3x^2+5x+10`
`=-3(x^2-5/3x)+10`
`=-3(x^2-5/3x+25/36-25/36)+10`
`=-3(x-5/6)^2+25/12+10`
`=-3(x-5/6)^2+145/12<=145/12`
Dấu "=" xảy ra khi`x=5/6`


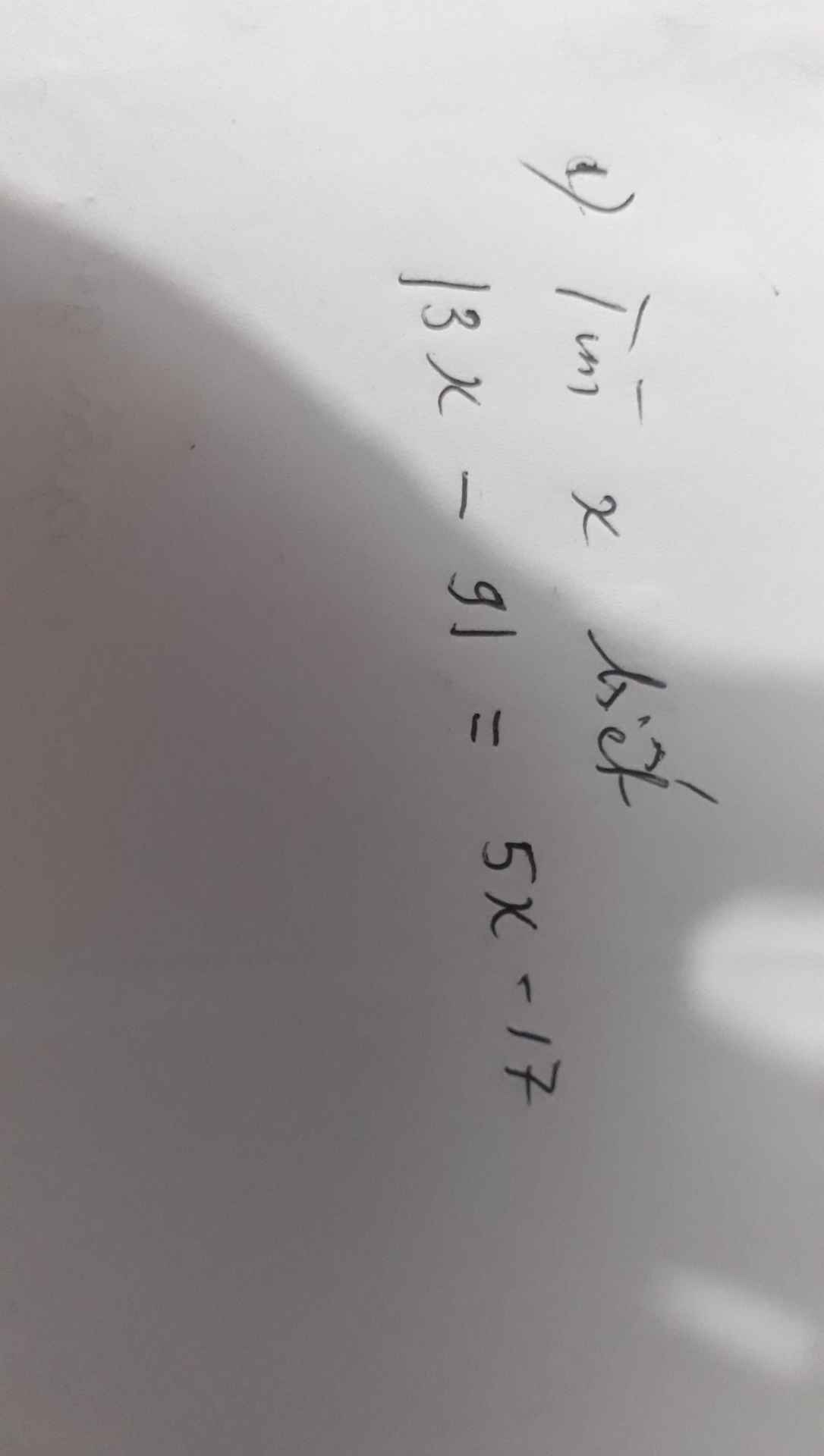

 giải hộ e với em cần gấp ạ
giải hộ e với em cần gấp ạ 
Rút gọn biểu thức sau: (2x – 3) (x + 5) - (2x² - 8)
\(\left(2x-3\right)\left(x+5\right)-\left(2x^2-8\right)\\ =2x^2+7x-15-2x^2+8\\ =\left(2x^2-2x^2\right)+7x+\left(-15+8\right)\\ =7x-7\)