
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



+)\(|\)x\(|\)<4 ma \(|\)x\(|\)\(\ge\)0\(\forall\)x
nên \(|\)x\(|\)\(\in\){0;1;2;3}
\(\Rightarrow\)x\(\in\){0;1;-1;2;-2;3;-3}
+)(x+2)(x-3)>0
nên x+2>0 và x-3>0 thì x>-2 và x>3 \(\Rightarrow\)x>3
hoặc x+2<0 và x-3<0 thì x<-2 và x<3 \(\Rightarrow\)x<-2
Vậy x>3 và x<-2
+)(x+2019)(x-25)=0
\(\Rightarrow\)x+2019=0 hoặc x-25=0
x=-2019 hoặc x=25
Vậy x=-2019;x=25
1 .=>x=4 hoặc x=-4
2. =>x+2>0 và x-3>0 hoặc x+2<0 và x-3 <0
=> x>-2 và x> 3 hoặc x<-2 và x <3
=>x>-2 và x<3
=>-2<x<3
=> x = -1,0,1,2
3. => x+2019 =0 hoặc x-25 =0
=> x = -2019 hoặc x = 25

|-17 - x | = 7
\(\Rightarrow\orbr{\begin{cases}-17-x=7\\-17-x=-7\end{cases}}\Rightarrow\orbr{\begin{cases}x=-24\\x=10\end{cases}}\)


Áp dụng bất đẳng thức \(\left|a\right|+\left|b\right|\ge\left|a+b\right|\) ta có:
\(A\ge\left|x+2+1-x\right|=\left|3\right|=3\)
Dấu " = " khi \(\left\{\begin{matrix}x+2\ge0\\1-x\ge0\end{matrix}\right.\Rightarrow\left\{\begin{matrix}x\ge-2\\x\le1\end{matrix}\right.\Rightarrow-2\le x\le1\)
\(\Rightarrow x\in\left\{-2;-1;0;1\right\}\)
Vậy \(MIN_A=3\) khi \(x\in\left\{-2;-1;0;1\right\}\)

tất cả đều có giá trị lớn nhất bằng 0
a.) tại x=-1
b.) tại x=-5
c.) tại x=-2
d.) tại x=3
a ) Vì |x + 1| ≥ 0 với mọi x
=> - |x + 1| ≤ 0 với mọi x
Dấu "=" xảy ra khi và chỉ khi |x + 1| = 0 => x = - 1
Vậy giá trị lớn nhất của A là 0 tại x = - 1
Các ý khác tương tự

/4-x/=/-7/
/4-x/=7
Xét 2 trường hợp
TH1: 4-x=7
x=-3
TH2: 4-X=-7
x=11
KL: X E {-3;11}
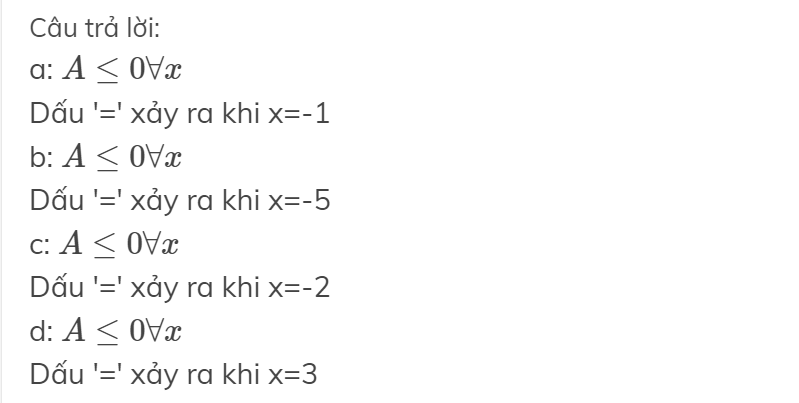
Áp dụng BĐT trị tuyệt đối, ta có:
\(\left|x-9\right|+\left|2-x\right|\ge\left|x-9+2-x\right|=\left|7\right|=7\)
Dấu "=" xảy ra khi: \(\left(x-9\right)\left(2-x\right)\ge0\)
\(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x-9\ge0\\2-x\ge0\end{matrix}\right.\\\left\{{}\begin{matrix}x-9\le0\\2-x\le0\end{matrix}\right.\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x\ge9\\x\le2\end{matrix}\right.\left(\text{vô lí}\right)\\\left\{{}\begin{matrix}x\le9\\x\ge2\end{matrix}\right.\end{matrix}\right.\\ \Rightarrow2\le x\le9\)
\(\left|x-9\right|+\left|2-x\right|=7\)
Ta có : \(\left|x-9\right|+\left|2-x\right|\ge\left|x-9+2-x\right|=7\)
Nên \(x=0\) là nghiệm phương trình đã cho.