Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì Om và On là hai tia nằm giữa hai tia Ox và Oy
=>mOnˆ=xOyˆ−xOmˆ−yOn^
⇔mOnˆ=1800−2yOnˆ
Mà Ot là tia phân giác của góc mOn
⇔tOn^=1/2(1800−2yOn^)
⇔tOnˆ=900−yOnˆ
Vì Ot là tia phân giác của góc mOn
=>tOyˆ=tOnˆ+yOnˆtOy^
⇔zOyˆ=900−yOnˆ
⇔tOyˆ=900
⇔Ot⊥xy

x O y m n z
Bài làm
Ta có: \(\widehat{xOy}=\widehat{xOm}+\widehat{yOn}+\widehat{mOz}+\widehat{zOn}\)
Mà \(\widehat{xOm}=\widehat{yOn}=2\widehat{xOm}\)
Oz là tia phân giác của \(\widehat{mOn}\)
=> \(\widehat{mOz}=\widehat{zOn}=2\widehat{mOz}\)
=> \(\widehat{xOy}=2\widehat{xOm}+2\widehat{mOz}\)
Hay \(180^0=2\widehat{xOm}+2\widehat{mOz}\)
=> \(180^0=2(\widehat{xOm}+\widehat{mOz})\)
=> \(\widehat{xOm}+\widehat{mOz}=180^0:2\)
=> \(\widehat{xOm}+\widehat{mOz}=90^0\)
Hay \(\widehat{xOz}=90^0\)
=> \(Oz\perp xy\)
Vậy \(Oz\perp xy\)( đpcm )
# Học tốt #

a,
\(\widehat{tOz}\) + \(\widehat{xOt}\) + \(\widehat{yOz}\) =1800
⇒\(\widehat{tOz}\) = 1800 - ( \(\widehat{xOt}\) + \(\widehat{yOz}\))
\(\widehat{tOz}\) = 1800 - (300 + 300) = 1200
b, Om là phân giác của góc \(x\)Oy vì:
\(\widehat{mOt}\) = \(\widehat{mOz}\) = \(\dfrac{1}{2}\) \(\widehat{xOz}\) (vì Om là phân giác của góc tOz)
⇒ \(\widehat{mOt}\) = \(\widehat{mOz}\) = 1200 : 2 = 600
\(\widehat{xOm}\) = \(\widehat{xOt}\) + \(mOt\) = 300 + 600 = 900
\(\widehat{mOy}\) = \(\widehat{mOz}\) + \(\widehat{yOz}\) = 300 + 600 = 900
⇒ \(\widehat{xOm}\) = \(\widehat{mOy}\) mà Om nằm giữa hai tia \(Ox\) và Oy
Nên Om là tia phân giác của góc \(x\)Oy

a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
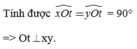
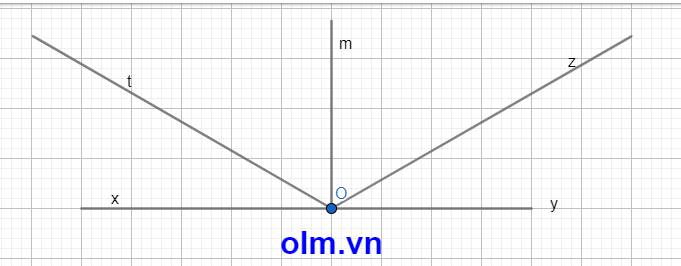
a) Do \(\widehat{xOy}\) là góc bẹt
=> \(\widehat{xOy}=180^o\)
Do On nằm giữa Ox và Oy
=> \(\widehat{xOn}+\widehat{nOy}=\widehat{xOy}\)
=> \(30^o+\widehat{yOn}=180^o\)
=> \(\widehat{yOn}=180^o-30^o\)
=> \(\widehat{yOn}=150^o\)
b) Ot là tia phân giác của \(\widehat{yOn}\)
=> \(\widehat{yOt}=\dfrac{1}{2}\widehat{nOy}=\dfrac{1}{2}.150^o=75^o\)
Do Ot nằm giữa Ox và Oy
=> \(\widehat{xOt}+\widehat{tOy}=\widehat{xOy}\)
=> \(\widehat{xOt}+75^o=180^o\)
=> \(\widehat{xOt}=180^o-75^o\)
=> \(\widehat{xOt}=105^o\)
a: \(\widehat{xOn}+\widehat{yOn}=180^0\)(hai góc kề bù)
=>\(\widehat{yOn}+30^0=180^0\)
=>\(\widehat{yOn}=180^0-30^0=150^0\)
b: Ot là phân giác của góc yOn
=>\(\widehat{yOt}=\dfrac{1}{2}\cdot\widehat{yOn}=\dfrac{1}{2}\cdot150^0=75^0\)
Ta có: \(\widehat{xOt}+\widehat{yOt}=180^0\)
=>\(\widehat{xOt}+75^0=180^0\)
=>\(\widehat{xOt}=105^0\)