Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi vận tốc dự định là x
Thời gian dự định là 90/x
Thời gian thực tế là 30/x+60/x-10
Theo đề ta có: 30/x+60/x-10-90/x=3/10
=>60/x-10-60/x=3/10
=>20/x-10-20/x=1/10
=>\(\dfrac{20x-20x+200}{x\left(x-10\right)}=\dfrac{1}{10}\)
=>x^2-10x-2000=0
=>x=50
Từ giả thiết suy ra AC = 10km; B ^ = 15 0
Xét tam giác ABC vuông tại A có:
Đáp án cần chọn là: A
Ta có: sin β = 10/300 = 1/30
Suy ra: β ≈ 1 ° 55 '
Vậy khi máy bay bắt đầu hạ cánh thì góc nghiêng là 1 ° 55 '
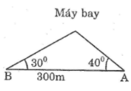
Gọi C là vị trí của máy bay
Gọi CH là độ cao của máy bay so với mặt đất
=>CH\(\perp\)AB tại H
Ta có hình vẽ sau:
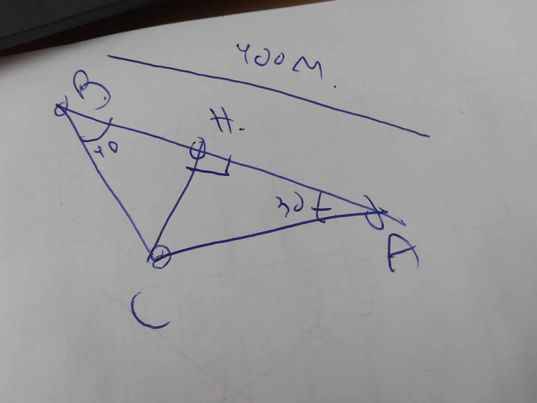
Xét ΔCBA có \(\widehat{CBA}+\widehat{CAB}+\widehat{ACB}=180^0\)
=>\(\widehat{ACB}+30^0+40^0=180^0\)
=>\(\widehat{ACB}=110^0\)
Xét ΔABC có \(\dfrac{BA}{sinACB}=\dfrac{AC}{sinB}=\dfrac{BC}{sinA}\)
=>\(\dfrac{400}{sin110}=\dfrac{AC}{sin40}=\dfrac{BC}{sin30}\)
=>\(AC\simeq273,62\left(m\right);BC\simeq212,84\left(m\right)\)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot CA\cdot CB\cdot sinACB\)
\(=\dfrac{1}{2}\cdot273,62\cdot212,84\cdot sin110\simeq27362,57\left(m^2\right)\)
Xét ΔACB có CH là đường cao
nên \(\dfrac{1}{2}\cdot CH\cdot AB=S_{ABC}\)
=>\(CH\cdot\dfrac{400}{2}=27362,57\)
=>\(CH\simeq136,81\left(m\right)\)
Độ cao của máy bay là CD, độ dài AB = 60m; D A C ^ = 30 0 ; D B C ^ = 50 0
Gọi BC = x => AC = 60 + x
Xét tam giác BDC vuông tại C có:
Xét tam giác ADC vuông tại C có:
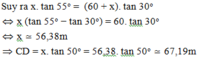
Vậy độ cao của máy bay so với mặt đất là 67,19m
Đáp án cần chọn là: C
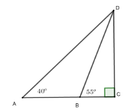
Độ cao của máy bay là CD, độ dài AB = 80m
Gọi BC = x (x > 0) => AC = 80 + x
Xét tam giác BDC vuông tại C có CD = x . tan 55 0
Xét tam giác ADC vuông tại C có CD = (80 + x). tan 44 0
Suy ra x . tan 55 0 = (80 + x). tan 44 0
=> x ≈ 113,96m
=> CD = 113,96. tan 55 0 ≈ 162,75m
Vậy độ cao của máy bay so với mặt đất là 162,75m
Đáp án cần chọn là: A
Gọi C là vị trí của máy bay.
Kẻ CH ⊥ AB
Trong tam giác vuông ACH, ta có:
AH = CH.cotgA (1)
Trong tam giác vuông BCH, ta có:
BH = CH.cotgB (2)
Từ (1) và (2) suy ra: (AH + BH) = CH.cotgA + CH.cotgB
Suy ra: CH =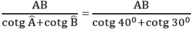 
≈ 102,606 (cm)
Do ngồi trên máy bay nên rõ ràng không thể nhìn qua hai hướng khác nhau nên hai thị trấn là cùng một phía so với chiếc máy bay
Giả sử AB là độ cao máy bay so với mặt đất (A ở đất). BC là khoảng cách máy bay đến thị trấn 1. BD là khoảng cách từ máy bay tới thị trấn 2.
Và: \(\left\{{}\begin{matrix}\widehat{BCA}=55^o\\\widehat{BDA}=28^o\end{matrix}\right.\)
Do tam giác `ABC` vuông tại `A =>` \(AC=\dfrac{AB}{tanBCA}=\dfrac{10}{tan55^o}\approx7\left(km\right)\)
Do tam giác `ABD` vuông tại `A =>` \(AD=\dfrac{AB}{tanBDA}=\dfrac{10}{tan28^o}\approx18,8\left(km\right)\)
`=> CD = 18,8 - 7 = 11,8 (km)`