HP
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
17 tháng 4 2017
a) \(\dfrac{-1}{-4}\)=\(\dfrac{1}{4}>0\)
\(\dfrac{3}{-4}< 0\)
\(\Rightarrow\dfrac{1}{4}>\dfrac{3}{-4}hay\dfrac{-1}{-4}>\dfrac{3}{-4}\)
b) Ta có:
\(\dfrac{15}{17}=1-\dfrac{2}{17}\\ \)
\(\dfrac{25}{27}=1-\dfrac{2}{27}\\ \\ \)
Mà \(\dfrac{2}{17}>\dfrac{2}{27}\left(17< 27\right)\)
\(\Rightarrow1-\dfrac{2}{17}< 1-\dfrac{2}{27}\)hay \(\dfrac{15}{17}< \dfrac{25}{27}\)
18 tháng 9 2017
a/ Ta có :
\(A=\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...........+\dfrac{1}{n^2}\)
Ta thấy :
\(\dfrac{1}{2^2}< \dfrac{1}{1.2}\)
\(\dfrac{1}{3^2}< \dfrac{1}{2.3}\)
.......................
\(\dfrac{1}{n^2}< \dfrac{1}{\left(n-1\right)n}\)
\(\Leftrightarrow A< \dfrac{1}{1.2}+\dfrac{1}{2.3}+...........+\dfrac{1}{\left(n-1\right)n}\)
\(\Leftrightarrow A< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+..........+\dfrac{1}{n-1}-\dfrac{1}{n}\)
\(\Leftrightarrow A< 1-\dfrac{1}{n}< 1\)
\(\Leftrightarrow A< 1\)
b/ Ta có :
\(B=\dfrac{1}{2^2}+\dfrac{1}{4^2}+\dfrac{1}{6^2}+.................+\dfrac{1}{\left(2n\right)^2}\)
\(=\dfrac{1}{4}\left(1+\dfrac{1}{2^2}+\dfrac{1}{4^2}+..........+\dfrac{1}{n^2}\right)\)
Ta thấy :
\(\dfrac{1}{2^2}< \dfrac{1}{1.2}\)
\(\dfrac{1}{3^2}< \dfrac{1}{2.3}\)
..................
\(\dfrac{1}{n^2}< \dfrac{1}{\left(n-1\right)n}\)
\(\Leftrightarrow B< \dfrac{1}{4}\left(1+\dfrac{1}{1.2}+\dfrac{1}{2.3}+.........+\dfrac{1}{\left(n-1\right)n}\right)\)
\(\Leftrightarrow B< \dfrac{1}{4}\left(1+1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+......+\dfrac{1}{n-1}-\dfrac{1}{n}\right)\)
\(\Leftrightarrow B< \dfrac{1}{4}\left(1+1-\dfrac{1}{n}\right)\)
\(\Leftrightarrow B< \dfrac{1}{2}-\dfrac{1}{4n}< \dfrac{1}{2}\)
\(\Leftrightarrow B< \dfrac{1}{2}\)
LN
19 tháng 9 2017
\(\)\(A=\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{n^2}\)
\(A< \dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{\left(n-1\right)n}\)
\(A< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{n-1}-\dfrac{1}{n}\)
\(A< 1-\dfrac{1}{n}< 1\)
\(B=\dfrac{1}{2^2}+\dfrac{1}{4^2}+\dfrac{1}{6^2}+...+\dfrac{1}{2n^2}\)
\(B=\dfrac{1}{2}\left(\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{2n^2}\right)\)
\(B=\dfrac{1}{4}+\dfrac{1}{2}\left(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{2n^2}\right)\)
\(B< \dfrac{1}{4}+\dfrac{1}{2}\left(\dfrac{1}{1.2}+\dfrac{1}{2.3}+.....+\dfrac{1}{\left(n-1\right)n}\right)\)
PH
21 tháng 4 2017
Vì 18/91 < 18/90 =1/5
23/114>23115=1/5
vậy 18/91<1/5<23/114
suy ra 18/91<23/114
PH
21 tháng 4 2017
vì 21/52=210/520
Mà 210/520=1-310/520
213/523=1-310/523
310/520>310/523
vậy 210/520<213/523
suy ra 21/52<213/523
25 tháng 7 2017
\(n\left(n+3\right)=n^2+3n\)
\(\left(n+2\right)\left(n+1\right)=n^2+3n+2\)
Vì \(n^2+3n< n^2+3n+2\Rightarrow\dfrac{n}{n+1}< \dfrac{n+2}{n+3}\left(n\in N\right)\)
b) \(\dfrac{n}{2n+1}=\dfrac{3n}{6n+3}< \dfrac{3n+1}{6n+3}\)
c) \(\dfrac{10^8+2}{10^8-1}=1+\dfrac{1}{10^8-1}\)
\(\dfrac{10^8}{10^8-3}=\left(1+\dfrac{3}{10^8-3}\right)\)
Vì \(\dfrac{1}{10^8-1}>\dfrac{3}{10^8-3}\Rightarrow\dfrac{10^8+2}{10^8-1}< \dfrac{10^8}{10^8-3}\)
PN
25 tháng 7 2017
Làm dần dần và làm từ từ, suy ra được nhiều cách giải.
a) \(\dfrac{n}{n+1}\) và \(\dfrac{n+2}{n+3}\)
+ Cách 1:
\(\dfrac{n}{n+1}=\dfrac{n+1-1}{n+1}=1-\dfrac{1}{n+1}\)
\(\dfrac{n+2}{n+3}=\dfrac{n+3-1}{n+3}=1-\dfrac{1}{n+3}\)
Vì \(\dfrac{1}{n+1}>\dfrac{1}{n+3}\) nên \(1-\dfrac{n}{n+1}< 1-\dfrac{1}{n+3}\)
\(\Rightarrow\dfrac{n}{n+1}< \dfrac{n+2}{n+3}\)
+ Cách 2:
Ta so sánh: \(n\left(n+3\right)\) và \(\left(n+1\right)\left(n+2\right)\)
\(n\left(n+3\right)=nn+3n=n^2+3n\)
\(\left(n+1\right)\left(n+2\right)=\left(n+1\right)n+\left(n+1\right).2=n^2+n+2n+2=n^2+3n+2\)
Vì \(n^2+3n< n^2+3n+2\) nên \(\dfrac{n}{n+1}< \dfrac{n+2}{n+3}\)
b) \(\dfrac{n}{2n+1}\) và \(\dfrac{3n+1}{6n+3}\)
Ta so sánh: \(n\left(6n+3\right)\) và \(\left(2n+1\right)\left(3n+1\right)\)
\(n\left(6n+3\right)=n.6n+3n=6n^2+3n\)
\(\left(2n+1\right)\left(3n+1\right)=\left(2n+1\right)3n+\left(2n+1\right)=6n^2+3n+2n+1=6n^2+5n+1\)
Vì \(6n^2+3n< 6n^2+5n+1\) nên \(\dfrac{n}{2n+1}< \dfrac{3n+1}{6n+3}\)
c) \(\dfrac{10^8+2}{10^8-1}\) và \(\dfrac{10^8}{10^8-3}\)
\(\dfrac{10^8+2}{10^8-1}=\dfrac{10^8-1+3}{10^8-1}=1+\dfrac{3}{10^8-1}\)
\(\dfrac{10^8}{10^8-3}=\dfrac{10^8-3+3}{10^8-3}=1+\dfrac{3}{10^8-3}\)
Vì \(\dfrac{3}{10^8-1}>\dfrac{3}{10^8-3}\) nên \(\dfrac{10^8+2}{10^8-1}>\dfrac{10^8}{10^8-3}\)
d) \(\dfrac{3^{17}+1}{3^{20}+1}\) và \(\dfrac{3^{20}+1}{3^{23}+1}\)
(đang tìm cách làm, và thêm vài cách khác)
6 tháng 3 2017
Ta có: \(\dfrac{1}{n}-\dfrac{1}{n+1}=\dfrac{n+1-n}{n\left(n+1\right)}=\dfrac{1}{n\left(n+1\right)}=\dfrac{1}{n}.\dfrac{1}{n+1}\)
Vậy tích hai phân số bằng hiệu của chúng
5 tháng 5 2017
e, D = 512+1 /513+ 1 < 1 => 512+1/ 513+1 < 512+1+4/ 513+1+4
= 512+5/ 513+5 = 5. (511+1) / 5. (512+1) = 511+1 / 512+1= E
Vậy D < E
18 tháng 3 2017
Bài 1:
a) \(\dfrac{1}{n\left(n+1\right)}=\dfrac{1}{n}-\dfrac{1}{n+1}\)
Quy đồng \(VP\) ta được:
\(VP=\dfrac{1}{n}-\dfrac{1}{n+1}\)
\(\Rightarrow VP=\dfrac{n+1}{n\left(n+1\right)}-\dfrac{n}{n\left(n+1\right)}\)
\(\Rightarrow VP=\dfrac{n+1-n}{n\left(n+1\right)}=\dfrac{1}{n\left(n+1\right)}\)
\(\Rightarrow VP=VT\)
Vậy \(\forall n\in Z,n>0\Rightarrow\dfrac{1}{n\left(n+1\right)}=\dfrac{1}{n}-\dfrac{1}{n+1}\) (Đpcm)
b) \(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{9.10}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{9}-\dfrac{1}{10}\)
\(=1-\dfrac{1}{10}\)
\(=\dfrac{9}{10}\)
18 tháng 3 2017
Bài 3:
a) \(\dfrac{1}{n}-\dfrac{1}{n+1}=\dfrac{1+1}{n\left(n+1\right)}-\dfrac{n}{n\left(n+1\right)}=\dfrac{1}{n\left(n+1\right)}\)
b) A=\(\dfrac{1}{2}.\dfrac{1}{3}+\dfrac{1}{3}.\dfrac{1}{4}+\dfrac{1}{4}.\dfrac{1}{5}+\dfrac{1}{5}.\dfrac{1}{6}+\dfrac{1}{6}.\dfrac{1}{7}+\dfrac{1}{7}.\dfrac{1}{8}+\dfrac{1}{8}.\dfrac{1}{9}\)
\(=\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{9}\)
\(=\dfrac{1}{2}-\dfrac{1}{9}\)
\(=\dfrac{7}{18}\)
B=\(\dfrac{1}{30}+\dfrac{1}{42}+\dfrac{1}{56}+\dfrac{1}{72}+\dfrac{1}{90}+\dfrac{1}{110}+\dfrac{1}{132}\)
\(=\dfrac{1}{5.6}+\dfrac{1}{6.7}+\dfrac{1}{7.8}+\dfrac{1}{8.9}+\dfrac{1}{9.10}+\dfrac{1}{10.11}+\dfrac{1}{11.12}\)
\(=\dfrac{1}{5}-\dfrac{1}{12}\)
\(=\dfrac{7}{60}\)
19 tháng 3 2017
a,Vế trái:
\(1-\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{2013}-\dfrac{1}{2014}\)
\(=1+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{2014}-2\left(\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{6}+...+\dfrac{1}{2014}\right)\)
\(=1+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{2014}-\left(1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{1007}\right)\)
\(=\dfrac{1}{1008}+\dfrac{1}{2009}+...+\dfrac{1}{2014}\)
b,chưa có câu trả lời, sorry nha
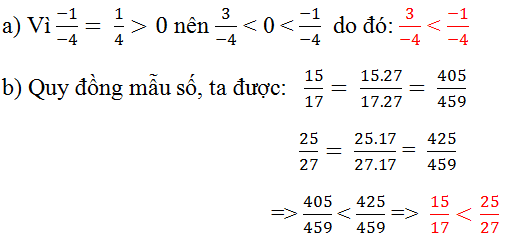
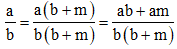
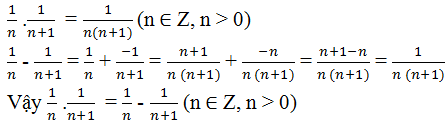
Vì n + 1 nên \(\dfrac{1}{n}>\dfrac{1}{n+1}\)
- Xét n = 0 hoặc n = -1 thì một trong 2 phân số đều không tồn tại
- Trong trường hợp 2 phân số đều có nghĩa thì `n < n+1`
=> \(\dfrac{1}{n}>\dfrac{1}{n+1}\)
------------------------------
Lưu ý: Phân số có cùng tử số thì mẫu phân số nào bé hơn thì giá trị phân số đó lớn hơn