Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
a) \(x=\frac{a+1}{a+9}=\frac{a+9-8}{a+9}=\frac{a+9}{a+9}-\frac{8}{a+9}=1-\frac{8}{a+9}\)
Để \(x\in Z\)thì \(a+9\inƯ\left(8\right)=\left\{-8;-4;-2;-1;1;2;4;8\right\}\)
Vậy \(a\in\left\{-17;-13;-11;-10;-8;-7;-5;-1\right\}\)
b) \(x=\frac{a-1}{a+4}=\frac{a+4-5}{a+4}=\frac{a+4}{a+4}-\frac{5}{a+4}=1-\frac{5}{a+4}\)
Để \(x\in Z\)thì \(a+4\inƯ\left(5\right)=\left\{-5;-1;1;5\right\}\)
Vậy \(a\in\left\{-9;-5;-3;1\right\}\)
Bài 2:
a) \(t=\frac{3x-8}{x-5}=\frac{3x-15}{x-5}+\frac{7}{x-5}=\frac{3\left(x-5\right)}{x-5}+\frac{7}{x-5}=3+\frac{7}{x-5}\)
Để \(t\in Z\)thì \(x-5\inƯ\left(7\right)=\left\{-7;-1;1;7\right\}\)
Vậy \(x\in\left\{-2;4;6;12\right\}\)
b)\(q=\frac{2x+1}{x-3}=\frac{2x-6}{x-3}+\frac{7}{x-3}=\frac{2\left(x-3\right)}{x-3}+\frac{7}{\left(x-3\right)}=2+\frac{7}{x-3}\)
Để \(q\in Z\)thì \(x-3\inƯ\left(7\right)=\left\{-7;-1;1;7\right\}\)
Vậy \(x\in\left\{-4;2;4;10\right\}\)
c)\(p=\frac{3x-2}{x+3}=\frac{3x+9}{x+3}-\frac{11}{x+3}=\frac{3\left(x+3\right)}{x+3}-\frac{11}{x+3}=3-\frac{11}{x+3}\)
Để \(p\in Z\)thì \(x+3\inƯ\left(11\right)=\left\{-11;-1;1;11\right\}\)
Vậy \(x\in\left\{-14;-4;-2;8\right\}\)
Bài 3:
Gọi \(d\inƯC\left(2m+9;14m+62\right)\)
\(\Rightarrow\hept{\begin{cases}\left(2m+9\right)⋮d\\\left(14m+62\right)⋮d\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}7\left(2m+9\right)⋮d\\\left(14m+62\right)⋮d\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}\left(14m+63\right)⋮d\\\left(14m+62\right)⋮d\end{cases}}\)
\(\Rightarrow\left[\left(14m+63\right)-\left(14m+62\right)\right]⋮d\)
\(\Rightarrow1⋮d\)
\(\Rightarrow d=1\)
\(\RightarrowƯC\left(2m+9;14m+62\right)=1\)
Vậy \(x=\frac{2m+9}{14m+62}\)là p/s tối giản

a) \(4^{x+2}.3^x=16.12^5\)
\(\Leftrightarrow4^{x+2}.3^x=4^2.4^5.3^5\)
\(\Leftrightarrow4^{x-5}.3^{x-5}=1\)
\(\Leftrightarrow12^{x-5}=1\)
\(\Leftrightarrow x-5=0\Leftrightarrow x=5\)
\(a)4^{x+2}.3^x=4^2.\left(4.3\right)^5\)
\(4^{x+2}.3^x=4^7.3^5\)
\(\Rightarrow4^{x+2}=4^7;3^x=3^5\)
\(\Rightarrow x=5\)
Vậy \(x=5\)

a)\(1,5:2,16=15:216=5:72\)
b)\(4\dfrac{2}{7}:\dfrac{3}{5}=\dfrac{30}{7}:\dfrac{3}{5}=\dfrac{30}{7}.\dfrac{5}{3}=\dfrac{50}{7}=50:7\)
c)\(\dfrac{\dfrac{2}{9}}{0,31}=\dfrac{2}{9}:\dfrac{31}{100}=\dfrac{2}{9}.\dfrac{100}{31}=\dfrac{31}{450}=31:450\)

\(a,\frac{x-7}{x-11}=\frac{\left(x-11\right)+4}{x-11}=1+\frac{4}{x-11}\)
Để phân số trên là số hữu tỉ âm\(\Rightarrow\frac{4}{x-11}< 0\)
\(\Rightarrow x-11< 0\)
\(\Rightarrow x< 11\)
\(2,\frac{x+2}{x-6}=\frac{x-6+8}{x-6}=1+\frac{8}{x-6}\)
Để phân số trên là số hữu tỉ âm \(\frac{\Rightarrow8}{x-6}< 1\Rightarrow x-6>8\Rightarrow x>14\)
\(3,\frac{x-3}{x+7}=\frac{x+7-10}{x+7}=1-\frac{10}{x+7}\)
Để phân số trên là số hữu tỉ âm\(\Rightarrow\frac{10}{x+7}< 1\Rightarrow x+7>10\Rightarrow x>3\)
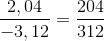
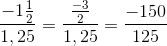
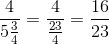
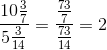
a) Để \(\dfrac{5}{x-3}\) là số hữu tỉ thì: \(x-3\ne0\Leftrightarrow x\ne3\)
=> \(x\in Z,x\ne3\)
b) Để \(\dfrac{-4}{5x+10}\) là số hữu tỉ thì: \(5x+10\ne0\Leftrightarrow5x\ne-10\Leftrightarrow x\ne-2\)
=> \(x\in Z,x\ne-2\)
Hình như đề bài sai rồi á bạn, mình nghĩ là tìm x nguyên để các số đó là số nguyên chứ.