Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

toán gì vậy,văn à?????????????????????????????????????????????????

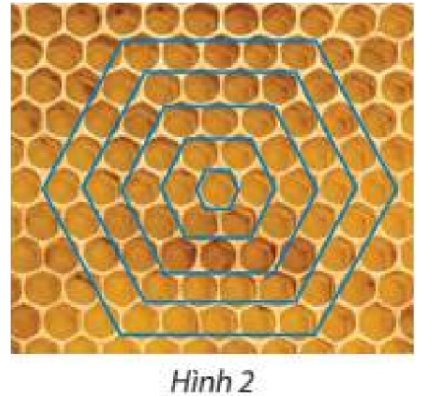
Dãy số chỉ số ô trên vòng là: \(u_1=6;u_2=12;u_3=18;...\)
Ta thấy: \(u_{n+1}=u_n+6\)
Vậy ô trên các vòng theo thứ tự tạo thành cấp số cộng có công sai d = 6.


Đáp án C
Trong 5 cạch còn lại (không kể cạnh AB) chỉ có 3 cạnh AD, DB, AC khi quay quanh trục AB tạo ra các hình nón. Do đó có 3 hình nón được tạo thành (như hình vẽ).
Chú ý: Do CB ⊥ (ADB) => CB ⊥ AB, do đó CB quay quanh AB chỉ tạo ra hình tròn mà không phải là hình nón.

Đáp án là C
Số cách chọn 2 số chẵn trong tập hợp 2 ; 4 ; 6 ; 8 là: C 4 2 cách.
Số cách chọn 2 số lẻ trong tập hợp 1 ; 3 ; 5 ; 7 ; 9 là: C 5 2 cách.
Số cách hoán vị 4 chữ số đã chọn lập thành 1 số tự nhiên là: 4! cách.
Vậy có 4 ! . C 4 2 . C 5 2 số tự nhiên thỏa mãn yêu cầu bài toán.

tham khảo:

Mô hình hoá cái hầm bằng cụt chóp tứ giác đều \(ABCD.A'B'C'D'\) với \(O,O'\) là tâm của hai đáy. Vậy \(AB = 14,A'B' = 10\).
Gọi \(M,M'\) lần lượt là trung điểm của \(CD,C'D'\).
\(A'B'C'{\rm{D}}'\) là hình vuông \( \Rightarrow O'M' \bot C'{\rm{D}}'\)
\(CDD'C'\) là hình thang cân \( \Rightarrow MM' \bot C'D'\)
Vậy \(\widehat {MM'O'}\) là góc nhị diện giữa mặt bên và đáy nhỏ.
\( \Rightarrow \widehat {MM'O'} = {135^ \circ } \Rightarrow \widehat {M'MO} = {180^ \circ } - \widehat {MM'O'} = {45^ \circ }\)
Kẻ \(M'H \bot OM\left( {H \in OM} \right)\)
\(OMM'O'\) là hình chữ nhật
\( \Rightarrow OH = O'M' = 5,MH = OM - OH = 2,M'H = OO' = MH.\tan {45^ \circ } = 2\)
Diện tích đáy lớn là: \(S = A{B^2} = {14^2} = 196\left( {{m^2}} \right)\)
Diện tích đáy bé là: \(S' = A'B{'^2} = {10^2} = 100\left( {{m^2}} \right)\)
Số mét khối đất cần phải di chuyển ra khỏi hầm là:
\(V = \frac{1}{3}h\left( {S + \sqrt {SS'} + S'} \right) = \frac{1}{3}.2\left( {196 + \sqrt {196.100} + 100} \right) = \frac{{872}}{3} \approx 290,67\left( {{m^3}} \right)\)

Xếp 30 quyển truyện khác nhau có số cách là 30!
Xếp 4 quyển 1, 3, 5, 7 cạnh nhau:
+) Hoán vị 1, 3, 5, 7 ta được 4! Cách.
+) Khi đã xếp 1, 3, 5, 7 cạnh nhau thì còn 26 vị trí, ứng với 26 vị trí này thì có 26! cách xếp.
Do đó xếp 4 quyển 1, 3, 5, 7 cạnh nhau có số cách là 4!.26!
Tóm lại có 30! – 4!26! cách xếp thỏa mãn.
Chọn B.

Chọn C
20 viên bi khác nhau được đánh số từ 1 đến 20, chia làm ba phần:
Phần 1 gồm các viên bi mang số chia hết cho 3, có 6viên.
Phần 2 gồm các viên bi mang số chia cho 3 dư 1, có 7 viên.
Phần 3 gồm các viên bi mang số chia cho 3 dư 2, có 7 viên.
Lấy ba viên bi từ hộp trên rồi cộng số ghi trên đó lại, được một số chia hết cho 3 có các trường hợp sau:
Trường hợp 1: lấy được 3 viên bi ở phần 1, có C 6 3 cách.
Trường hợp 2: lấy được 3 viên bi ở phần 2, có C 7 3 cách.
Trường hợp 3: lấy được 3 viên bi ở phần 3, có C 7 3 cách.
Trường hợp 4: lấy được 1 viên bi ở phần 1, 1 viên bi ở phần 2 và 1 viên bi ở phần 3, có C 6 1 . C 7 1 . C 7 1 cách.
Vậy có ![]() cách lấy được ba viên bi thỏa mãn yêu cầu bài toán.
cách lấy được ba viên bi thỏa mãn yêu cầu bài toán.

Đáp án A.
Hình đa diện đều có tất cả các mặt là ngũ giác có 30 cạnh.


Số kiểu chậu khác nhau là \(\dfrac{A^5_{20}}{5}=372096\) (chọn 5 số có kể thứ tự từ 20 số và chia cho số hoán vị vòng quanh của mỗi hoán vị phân biệt)