Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gợi ý: Sử dụng tính chất phân phối của phép nhân đối với phép cộng để nhóm thừa số chung ra ngoài.

\(A=11\dfrac{3}{13}-\left(2\dfrac{4}{7}+5\dfrac{3}{13}\right)\)
\(A=11\dfrac{3}{13}-5\dfrac{3}{13}-2\dfrac{4}{7}\)
\(A=6-2\dfrac{4}{7}\)
\(A=5\dfrac{7}{7}-2\dfrac{4}{7}\)
\(A=3\dfrac{3}{7}\)
\(B=\left(6\dfrac{4}{9}+3\dfrac{7}{11}\right)-4\dfrac{4}{9}\)
\(B=\left(6\dfrac{4}{9}-4\dfrac{4}{9}\right)+3\dfrac{7}{11}\)
\(B=2+3\dfrac{7}{11}\)
\(B=5\dfrac{7}{11}\)
\(C=\dfrac{-5}{7}.\dfrac{2}{11}+\dfrac{-5}{7}-\dfrac{9}{11}+1\dfrac{5}{7}\)
\(C=\dfrac{-5}{7}.\left(\dfrac{2}{11}+1\right)-\dfrac{9}{11}+1\dfrac{5}{7}\)
\(C=\dfrac{-5}{7}.\dfrac{13}{11}-\dfrac{9}{11}+1\dfrac{5}{7}\)
\(C=\dfrac{-65}{77}-\dfrac{9}{11}+1\dfrac{5}{7}\)
\(C=\dfrac{4}{11}+1\dfrac{5}{7}\)
\(C=\dfrac{160}{11}\)
\(D=0,7.2\dfrac{2}{3}.20.0,375.\dfrac{5}{28}\)
\(D=\dfrac{7}{10}.\dfrac{8}{3}.20.\dfrac{375}{1000}.\dfrac{5}{28}\)
\(D=\dfrac{7}{28}=\dfrac{5}{2}\)
\(E=\left(-6,17+3\dfrac{5}{9}-2\dfrac{36}{97}\right)\left(\dfrac{1}{3}-0,25-\dfrac{1}{12}\right)\)
\(E=\left(-6,17+3\dfrac{5}{9}-2\dfrac{36}{97}\right)\left(\dfrac{1}{3}-\dfrac{1}{4}-\dfrac{1}{12}\right)\)
\(E=\left(-6,17+3\dfrac{5}{9}-2\dfrac{36}{97}\right)\left(\dfrac{1}{12}-\dfrac{1}{12}\right)\)
\(E=\left(-6,17+3\dfrac{5}{9}-2\dfrac{36}{97}\right).0\)
\(\Rightarrow E=0\)

a) \(\dfrac{1}{6};\dfrac{1}{3};\dfrac{1}{2};...\)
\(\Rightarrow\dfrac{1}{6};\dfrac{2}{6};\dfrac{3}{6};...\)
Dãy có quy luật tăng dần lên 1 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{4}{6}\)
b) \(\dfrac{1}{8};\dfrac{5}{24};\dfrac{7}{24};...\)
\(\Rightarrow\dfrac{3}{24};\dfrac{5}{24};\dfrac{7}{24};...\)
Dãy có quy luật tăng dần lên 2 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{9}{24}\)
c) \(\dfrac{1}{5};\dfrac{1}{4};\dfrac{1}{3};...\)
\(\dfrac{4}{20};\dfrac{5}{20};\dfrac{6}{20};...\)
Dãy có quy luật tăng dần lên 1 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{7}{20}\)
d) \(\dfrac{4}{15};\dfrac{3}{10};\dfrac{1}{3};...\)
\(\Rightarrow\dfrac{8}{30};\dfrac{9}{30};\dfrac{11}{30};...\)
Dãy có quy luật tăng dần lên 1 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{12}{30}\)

\(A=\dfrac{6}{7}+\dfrac{1}{7}.\dfrac{2}{7}+\dfrac{1}{7}.\dfrac{5}{7}.\)
\(A=\dfrac{6}{7}+\dfrac{1}{7}\left(\dfrac{2}{7}+\dfrac{5}{7}\right).\)
\(A=\dfrac{6}{7}+\dfrac{1}{7}.1.\)
\(A=\dfrac{6}{7}+\dfrac{1}{7}=1.\)
Vậy \(A=1.\)
\(B=\dfrac{40}{9}.\dfrac{13}{3}-\dfrac{4}{3}.\dfrac{40}{9}.\)
\(B=\dfrac{4}{9}.\dfrac{13}{3}-\dfrac{4}{9}.\dfrac{40}{3}.\)
\(B=\dfrac{4}{9}\left(\dfrac{13}{3}-\dfrac{40}{3}\right).\)
\(B=\dfrac{4}{9}.\left(-9\right).\)
\(B=-4.\)
Vậy \(B=-4.\)

ính giá trị của các biểu thức sau:
A=827−(349+427)A=827−(349+427)
B=(1029+235)−629B=(1029+235)−629
Giải:
A=827−(349+427)A=827−(349+427)
=587−(319+307)=58−307−319=4−319=587−(319+307)=58−307−319=4−319
= 36−319=5936−319=59
B=(1029+235)−629B=(1029+235)−629
=1029−629+235=4+235=635
ính giá trị của các biểu thức sau:
A
=
8
2
7
−
(
3
4
9
+
4
2
7
)
A=827−(349+427)
B
=
(
10
2
9
+
2
3
5
)
−
6
2
9
B=(1029+235)−629
Giải:
A
=
8
2
7
−
(
3
4
9
+
4
2
7
)
A=827−(349+427)
=
58
7
−
(
31
9
+
30
7
)
=
58
−
30
7
−
31
9
=
4
−
31
9
=587−(319+307)=58−307−319=4−319
=
36
−
31
9
=
5
9
36−319=59
B
=
(
10
2
9
+
2
3
5
)
−
6
2
9
B=(1029+235)−629
=
10
2
9
−
6
2
9
+
2
3
5
=
4
+
2
3
5
=
6
3
5
Xem thêm tại: http://loigiaihay.com/bai-100-trang-47-sgk-toan-6-tap-2-c41a24737.html#ixzz4eUGN0ooE

b: \(C=\left(\dfrac{12}{199}+\dfrac{23}{200}-\dfrac{34}{201}\right)\cdot\dfrac{3-2-1}{6}=0\)

a)
b) Mẫu số chung là BCNN (5, 6) = 30. Do đó:
c) Mẫu số chung là BCNN (7, 15) = 105. Do đó:
a) −55,87−55,87
Rút gọn: −55=−1−55=−1
MC: 7
Quy đồng ta được:
−1=−77−1=−77 và 8787
b) 3,−35,−563,−35,−56
MC: 30
Thừa số phụ thứ nhất là: 30: 1 = 30
Thừa số phụ thứ hai là: 30 : 5 = 6
Thừa số phụ thứ ba là: 30 : 6 = 5
Quy đồng ta được:
3=31=3.303=903−35=(−3).65.6=−1830−56=(−5).56.5=−25303=31=3.303=903−35=(−3).65.6=−1830−56=(−5).56.5=−2530
c) −97,−1915,−1−97,−1915,−1
MC: 15. 7 = 105
Thừa số phụ thứ nhất là: 105 : 7 = 15
Thừa số phụ thứ hai là: 105 : 15 = 7
Thừa số phụ thứ ba là: 105 : 1 = 105
Quy đồng ta được:
−97=(−9).157.15=−135105−1915=(−19).715.7=−133105−1=−11=(−1).1051.105=−105105−97=(−9).157.15=−135105−1915=(−19).715.7=−133105−1=−11=(−1).1051.105=−105105

Áp dụng tính chất phân phối, rồi tính giá trị biểu thức.
Chẳng hạn,
Với , thì
ĐS. ; C = 0.
Xem thêm tại: http://loigiaihay.com/bai-77-trang-39-phan-so-hoc-sgk-toan-6-tap-2-c41a5943.html#ixzz4eU1fQCGw
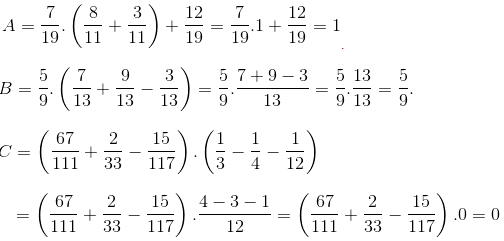
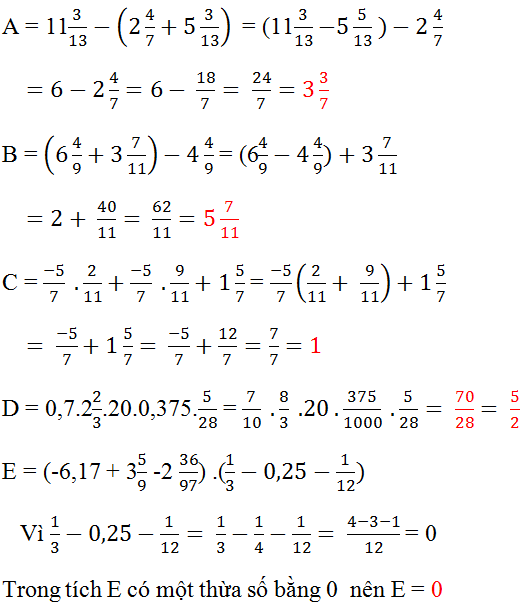


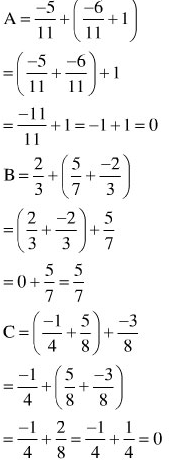
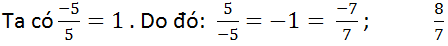
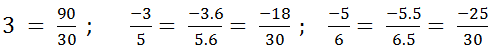
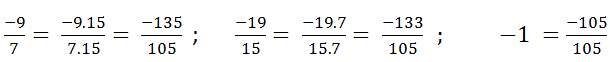
bằng 6,486242254 nha
cách trình bày đâu bạn ???