Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Hệ số biến dạng theo mỗi trục đo O'x', O'y', O'z' lần lượt là:
p=O'A'OA=22=1�=�'�'��=22=1;
q=O'B'OB=13�=�'�'��=13;
r=O'C'OC=46=23�=�'�'��=46=23.
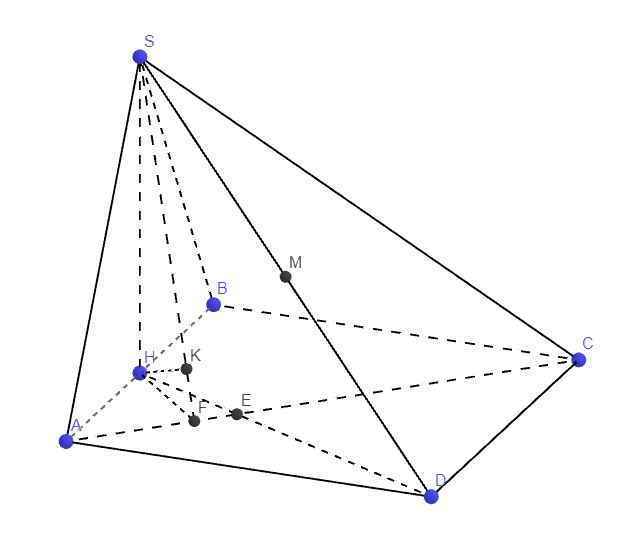
Gọi H là trung điểm AB, có lẽ từ 2 câu trên ta đã phải chứng minh được \(SH\perp\left(ABCD\right)\)
Do \(\left\{{}\begin{matrix}DM\cap\left(SAC\right)=S\\MS=\dfrac{1}{2}DS\end{matrix}\right.\) \(\Rightarrow d\left(M;\left(SAC\right)\right)=\dfrac{1}{2}d\left(D;\left(SAC\right)\right)\)
Gọi E là giao điểm AC và DH
Talet: \(\dfrac{HE}{DE}=\dfrac{AH}{DC}=\dfrac{1}{2}\Rightarrow HE=\dfrac{1}{2}DE\)
\(\left\{{}\begin{matrix}DH\cap\left(SAC\right)=E\\HE=\dfrac{1}{2}DE\end{matrix}\right.\) \(\Rightarrow D\left(H;\left(SAC\right)\right)=\dfrac{1}{2}d\left(D;\left(SAC\right)\right)=d\left(M;\left(SAC\right)\right)\)
Từ H kẻ HF vuông góc AC (F thuộc AC), từ H kẻ \(HK\perp SF\)
\(\Rightarrow HK\perp\left(SAC\right)\Rightarrow HK=d\left(H;\left(SAC\right)\right)\)
ABCD là hình vuông \(\Rightarrow\widehat{HAF}=45^0\Rightarrow HF=AH.sin45^0=\dfrac{a\sqrt{2}}{4}\)
\(SH=\dfrac{a\sqrt{3}}{2}\), hệ thức lượng:
\(HK=\dfrac{SH.HF}{\sqrt{SH^2+HF^2}}=\dfrac{a\sqrt{21}}{14}\)
\(\Rightarrow d\left(M;\left(SAC\right)\right)=\dfrac{a\sqrt{21}}{14}\)
giúp mình với ạ
ta có chu kỳ của hàm số bằng \(\frac{\pi}{3}\)
mà ta có :\(tan3x\text{ có chu kỳ là }\frac{2\pi}{3}\), \(cotmx\text{ có chu kỳ là }\frac{2\pi}{m}\)
vậy \(\frac{\pi}{3}\text{ là UCLN của }\left(\frac{2\pi}{3},\frac{2\pi}{m}\right)\Rightarrow m=6\)
thay lại thấy thỏa mãn, vậy m=6
@Nguyễn Minh Quang Cảm ơn b đã trả lời, nhưng hình như chu kỳ của tan3x là pi/3 đúng không ạ?
đây là phương trình tổ hợp ,mọi người giúp mình với, mình phải kiểm tra gấp 
Câu 13:
Ta có công thức lãi kép: \(C=A\left(1+r\right)^N\) với C là số tiền thu được (cả vốn lẫn lãi); A là số tiền gửi; r là lãi suất mỗi kì, N là số kì.
a) Sau 2 năm số tiền cả vốn lẫn lãi ở quyển 1 là \(100\left(1+6,8\%\right)^2=114,0624\approx114\) (triệu đồng)
\(\Rightarrow\) Khẳng định đúng
b) Sau 2 năm số tiền cả vốn lẫn lãi ở quyển 2 là \(100\left(1+6\%\right)^2=112,36\) (tr đồng)
Suy ra số tiền ở cả 2 quyển là \(114,0624+112,36=226,4224\) (tr đồng)
\(\Rightarrow\) Khẳng định đúng.
c) Số tiền gửi sau \(N\) năm (kì) là:
\(C=100\left(1+6,8\%\right)^N+100\left(1+6\%\right)^N\)
Thế \(N\ge8\), ta có \(C\ge100\left[\left(1+6.8\%\right)^8+\left(1+6\%\right)^8\right]\approx328,65>300\)
\(\Rightarrow\) Khẳng định đúng.
d) Ta nhắc lại rằng nếu theo ban đầu, sau 2 năm thì số tiền thu được sẽ là \(226,4224\) tr đồng.
Theo tình huống mới, số tiền sau năm đầu ở quyển 1, 2 lần lượt là \(114,0624\) tr đồng và \(112,36\) tr đồng. Sau khi lấy 1 nửa số tiền từ đây chuyển sang quyển 2 thì lúc này quyển 1 còn \(57,0312\) tr đồng và quyển 2 có \(169,3912\) tr đồng. Sau năm thứ 2, quyển 1 có \(57,0312\left(1+6,8\%\right)=60,9093216\) (tr đồng), quyển 2 có \(169,3912\left(1+6\%\right)=179,554672\) (tr đồng). Do vậy cả 2 quyển có \(179,554672+60,9093216=240,4639936\) (tr đồng)
\(\Rightarrow\) Khẳng định đúng.
Câu 14:
a) \(\lim\limits_{x\rightarrow1}f\left(x\right)=\lim\limits_{x\rightarrow1}\dfrac{2-\sqrt{2-x}}{x+2}=\dfrac{2-\sqrt{2-1}}{1+2}=f\left(1\right)\) => Khẳng định đúng.
b) \(\lim\limits_{x\rightarrow-\infty}f\left(x\right)=\lim\limits_{x\rightarrow-\infty}\left(x^2+ax+2\right)=+\infty\) => Khẳng định sai.
c) \(\lim\limits_{x\rightarrow-2^+}f\left(x\right)=\lim\limits_{x\rightarrow-2^+}\dfrac{2-\sqrt{2-x}}{x+2}\) \(=\lim\limits_{x\rightarrow-2^+}\dfrac{4-\left(2-x\right)}{\left(x+2\right)\left(2+\sqrt{2-x}\right)}\)
\(=\lim\limits_{x\rightarrow-2^+}\dfrac{1}{2+\sqrt{2-x}}\) \(=\dfrac{1}{2+\sqrt{2-\left(-2\right)}}=\dfrac{1}{4}\)
=> Khẳng định đúng.
d) Ta có \(\lim\limits_{x\rightarrow-2^+}f\left(x\right)=\dfrac{1}{4}\) và \(\lim\limits_{x\rightarrow-2^-}f\left(x\right)=\lim\limits_{x\rightarrow-2^-}\left(x^2+ax+2\right)=4-2a+2\)
Để tồn tại \(\lim\limits_{x\rightarrow-2}f\left(x\right)\) thì \(4-2a+2=\dfrac{1}{4}\) \(\Leftrightarrow a=\dfrac{23}{8}\)
Có \(\lim\limits_{x\rightarrow2^-}f\left(x\right)=\lim\limits_{x\rightarrow2^-}\dfrac{2-\sqrt{2-x}}{x+2}=\dfrac{1}{2}\)
\(\lim\limits_{x\rightarrow2^+}f\left(x\right)=\lim\limits_{x\rightarrow2^+}\left(x+a-b\right)=2+a-b\)
Để tồn tại \(\lim\limits_{x\rightarrow2}f\left(x\right)\) thì \(2+a-b=\dfrac{1}{2}\) \(\Leftrightarrow b=a+\dfrac{3}{2}=\dfrac{35}{8}\)
Khi đó \(4\left(a+b\right)=4\left(\dfrac{23}{8}+\dfrac{35}{8}\right)=29\)
=> Khẳng định đúng