OLM ưu đãi đặc biệt gói SVIP 18 THÁNG dành cho nhà trường, đăng kí ngay!

Tham gia ngay Cuộc thi "Đi tìm Đại sứ OLM" giải thưởng tới 10 triệu đồng

K
Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
TC
Thầy Cao Đô
Giáo viên VIP
8 tháng 12 2023 - olm

Bài 2. Trong nội dung thi điền kinh, bơi lội và đua xe đạp phối hợp được diễn ra tại một hồ bơi có chiều rộng $70$ m và chiều dài $250$ m. Một vận động viên cần chạy phối hợp với bơi (bắt buộc cả hai) khi phải thực hiện lộ trình xuất phát từ $A$ đến $C$ và đua xe đạp tới $D$ như hình vẽ.

loading...

Lập hàm số biểu thị thời gian hoàn thành nội dung bài thi của vận động viên. Biết rằng vận tốc của vận động viên khi chạy trên bờ, khi bơi và khi đua xe lần lượt là $5$ m/s, $1,5$ m/s và $10$ m/s.
#Toán lớp 10
2
NT
Nguyễn Thiên Hương
11 tháng 12 2023

loading... 

Đúng(0)
NM
Nguyễn Mai Trang
14 tháng 12 2023

loading... 

Đúng(0)
NP
NGÔ PHÚ HƯNG
28 tháng 10 2021 - olm
Từ hai điểm A và B trên một đường thẳng, có hai xe cùng chuyển động. Xe máy xuất phát từ A, chuyển động nhanh dần đều với gia tốc 0,1m/s2 để đến B. Cùng lúc xe máy xuất phát từ A, một xe đạp chuyển động thẳng đều từ B với tốc độ 14,4km/h ngược chiều chuyển động của xe máy. Cho AB = 400m. Chọn gốc tọa độ tại A, chiều dương từ A đến B, mốc thời gian lúc xe máy xuất phát từ...
Đọc tiếp

Từ hai điểm A và B trên một đường thẳng, có hai xe cùng chuyển động. Xe máy xuất phát từ A, chuyển động nhanh dần đều với gia tốc 0,1m/s2 để đến B. Cùng lúc xe máy xuất phát từ A, một xe đạp chuyển động thẳng đều từ B với tốc độ 14,4km/h ngược chiều chuyển động của xe máy. Cho AB = 400m. Chọn gốc tọa độ tại A, chiều dương từ A đến B, mốc thời gian lúc xe máy xuất phát từ A. 
a. Lập phương trình chuyển động của hai xe? 
b. Tìm thời điểm và vị trí hai xe gặp nhau? khi đó vận tốc xe máy bằng bao nhiêu?
c. Khi xe máy đến B thì xe đạp còn cách điểm B bao nhiêu? 

 
#Toán lớp 10
0
QT
Quoc Tran Anh Le
Giáo viên
24 tháng 9 2023

Một vận động viên chạy xe đạp trong 1 giờ 30 phút đầu với vận tốc trung bình là 42km/h. Sau đó người này nghỉ tại chỗ 15 phút và tiếp tục đạp xe 2 giờ liền với vận tốc 30 km/h.

a) Hãy biểu thị quãng đường s (tính bằng kilômét) mà người này đi được sau t phút bằng một hàm số.

b) Vẽ đồ thị biểu diễn hàm số s theo t.
#Toán lớp 10
1
KS
Kiều Sơn Tùng
24 tháng 9 2023

Tham khảo:

a) Đổi: 1 giờ 30 phút = 1,5 giờ; 15 phút = 0,25 giờ; t phút = \(\frac{t}{{60}}\) giờ

Nếu \(t \le 90\)(phút) thì quãng đường s mà người đó đi được là: \(42.\frac{t}{{60}} = 0,7t\)(km)

Nếu \(90 < t \le 90 + 15 = 105\)(phút) thì quãng đường s mà người đó đi được là: \(42.1,5 = 63\)(km)

Nếu \(105 < t \le 105 + 120 = 225\)(phút) thì quãng đường s mà người đó đi được là: \(42.1,5 + (\frac{t}{{60}} - 1,5 - 0,25).30 = 0,5t + 10,5.\)(km)

Như vậy hàm số tính quãng đường s (km) sau t phút là:

\(s = \left\{ \begin{array}{l}0,7t\quad \quad \quad \quad (0 \le t \le 90)\\63\quad \quad \quad \quad \;\;\;(90 < t \le 105)\\0,5t + 10,5\quad \;\;(105 < t \le 225)\end{array} \right.\)

b)

Với \(0 \le t \le 90\) thì \(s = 0,7t\)

Trên đoạn [0;90] ta vẽ đường thẳng \(s = 0,7t\)

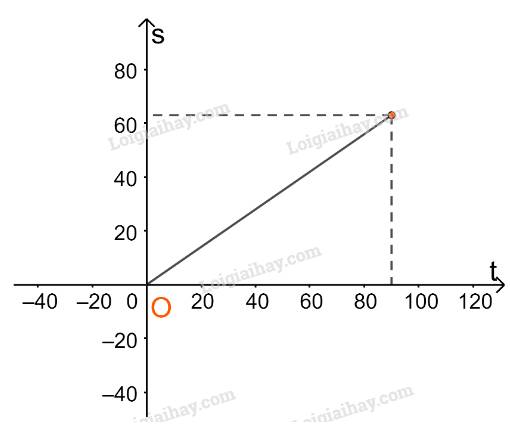
Với \(90 < t \le 105\) thì \(s = 63(km)\)

Trên nửa khoảng (90;105] ta vẽ đường thẳng \(s = 63\)

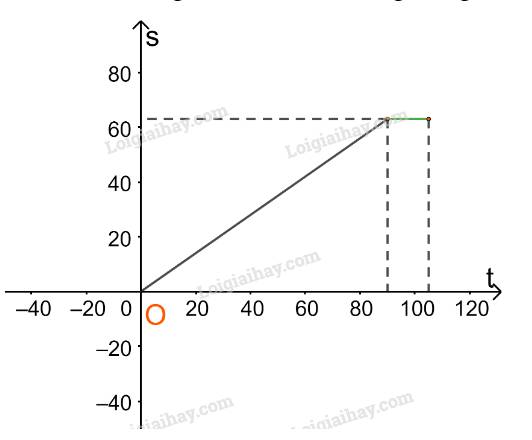
Với \(105 < t \le 225\)(phút) thì \(s = 0,5t + 10,5.\)(km)

Trên nửa khoảng (105;225] ta vẽ đường thẳng \(s = 0,5t + 10,5.\)

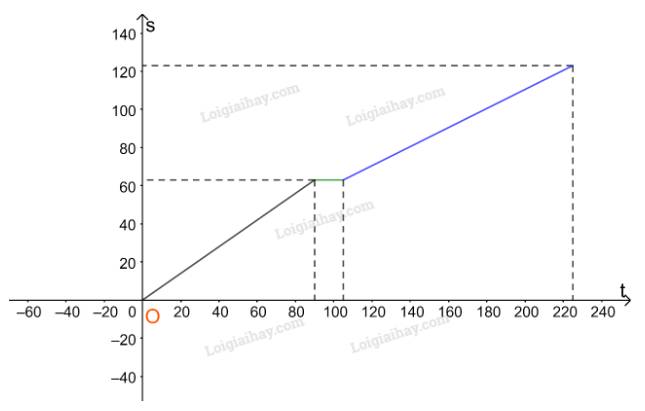
Như vậy ta được đồ thị biểu diễn hàm số s theo t như hình trên.

Đúng(0)
QT
Quoc Tran Anh Le
Giáo viên
26 tháng 9 2023
Một trò chơi đua xe ô tô vượt da mặt trên máy tính là xác định trước một hệ trục tọa độ Oxy. Cho biết một ô tô chuyển động thẳng đều từ điểm \(M(1;1)\) với Vectơ vận tốc\(\overrightarrow v  = (40;30)\)a) Viết phương trình tham số của đường thẳng d biểu diễn đường đi của ô tôb) Tìm tọa độ của xe tương ứng với t = 2; t =...
Đọc tiếp

Một trò chơi đua xe ô tô vượt da mặt trên máy tính là xác định trước một hệ trục tọa độ Oxy. Cho biết một ô tô chuyển động thẳng đều từ điểm \(M(1;1)\) với Vectơ vận tốc\(\overrightarrow v  = (40;30)\)

a) Viết phương trình tham số của đường thẳng d biểu diễn đường đi của ô tô

b) Tìm tọa độ của xe tương ứng với t = 2; t = 4
#Toán lớp 10
1
HQ
Hà Quang Minh
Giáo viên
26 tháng 9 2023

a) Phương trình tham số của đường thẳng \(d:\left\{ \begin{array}{l}x = 1 + 40t\\y = 1 + 30t\end{array} \right.\)

b) Thay \(t = 2\) vào phương trình\(d:\left\{ \begin{array}{l}x = 1 + 40t\\y = 1 + 30t\end{array} \right.\)  ta được \(\left\{ \begin{array}{l}x = 1 + 40.2 = 81\\y = 1 + 30.2 = 61\end{array} \right.\)

Vậy khi \(t = 2\) thì tọa độ của ô tô là \(\left( {81;61} \right)\)

Thay \(t = 4\) vào phương trình\(d:\left\{ \begin{array}{l}x = 1 + 40t\\y = 1 + 30t\end{array} \right.\)  ta được \(\left\{ \begin{array}{l}x = 1 + 40.4 = 161\\y = 1 + 30.4 = 121\end{array} \right.\)

Vậy khi \(t = 4\) thì tọa độ của ô tô là \(\left( {161;121} \right)\)

Đúng(0)
TQ
tao quen roi
27 tháng 6 2016
.Cùng một thời điểm, một chiếc ô tô XA xuất phát từ thành phố A về hướng thành phố B và một chiếc khác XB xuất phát từ thành phố B về hướng thành phố A. Chúng chuyển động với vận tốc riêng không đổi và gặp nhau lần đầu tại một điểm cách A là 20 km. Cả hai chiếc xe sau khi đến B và A tương ứng, lập tức quay trở lại và chúng gặp nhau lần thứ hai tại một điểm C. Biết thời...
Đọc tiếp

.Cùng một thời điểm, một chiếc ô tô XA xuất phát từ thành phố A về hướng thành phố B và một chiếc khác XB xuất phát từ thành phố B về hướng thành phố A. Chúng chuyển động với vận tốc riêng không đổi và gặp nhau lần đầu tại một điểm cách A là 20 km. Cả hai chiếc xe sau khi đến B và A tương ứng, lập tức quay trở lại và chúng gặp nhau lần thứ hai tại một điểm C. Biết thời gian xe XB đi từ C đến B là 10 phút và thời gian giữa hai lần gặp nhau là 1 giờ. Hãy tính vận tốc của từng chiếc ô tô
#Toán lớp 10
2
CW
Cold Wind
24 tháng 4 2017

không hiểu nổi tại sao lại là 2 lần đường.

XA XB A B C : Lần gặp 1 c: lần gặp 2 xe XA còn qua đoạn CA nữa mới đủ 2 lần xe XB còn qua đoạn CB nữa mới đủ 2 lần tính đến lúc gặp nhau lần 2

Xin lỗi, vì khi cái này đăng lên, câu hỏi trên sẽ bị loại khỏi danh sách "chưa trả lời"

Đúng(0)
TQ
tao quen roi
25 tháng 4 2017

?

Đúng(0)
QT
Quoc Tran Anh Le
Giáo viên
29 tháng 9 2023
Trong thực tiễn, có những tình huống đòi hỏi chúng ta phải xác định vị trí tương đối của hai đường thẳng, giao điểm của hai đường thẳng, … Chẳng hạn: Ở môn thể thao nội dung 10 m súng trường hơi di động, mục tiêu di động trên một đường thẳng b song song với mặt đất 1,4 m; viên đạn di động trên một đường thẳng a (Hình 39). Để bắn trúng mục tiêu, vận động viên phải ước...
Đọc tiếp

Trong thực tiễn, có những tình huống đòi hỏi chúng ta phải xác định vị trí tương đối của hai đường thẳng, giao điểm của hai đường thẳng, … Chẳng hạn: Ở môn thể thao nội dung 10 m súng trường hơi di động, mục tiêu di động trên một đường thẳng b song song với mặt đất 1,4 m; viên đạn di động trên một đường thẳng a (Hình 39). Để bắn trúng mục tiêu, vận động viên phải ước lượng được giao điểm M của a và b sao cho thời gian chuyển động đến điểm M của viên đạn và của mục tiêu là bằng nhau.

Làm thế nào để xác định giao điểm M của hai đường thẳng a và b?
#Toán lớp 10
1
HQ
Hà Quang Minh
Giáo viên
29 tháng 9 2023

Để xác định điểm M ta cần giải hệ phương trình gồm hai phương trình đường thẳng của hai đường thẳng a và b

Đúng(0)
TC
Thầy Cao Đô
Giáo viên VIP
10 tháng 2 2022 - olm
Cho hai tập khác rỗng $A = (m - 2; \, 6]$ và $B = (-2 ; \, 2m + 2)$ với $m \in \mathbb{R}$. Xác định $m$ để:  $A \cap B \ne \varnothing$;  $A \subset B$;  $B \subset A$;  $(A \cap B) \subset (-1 ; \,...
Đọc tiếp

Cho hai tập khác rỗng $A = (m - 2; \, 6]$ và $B = (-2 ; \, 2m + 2)$ với $m \in \mathbb{R}$. Xác định $m$ để:

loading... $A \cap B \ne \varnothing$;

loading... $A \subset B$;

loading... $B \subset A$;

loading... $(A \cap B) \subset (-1 ; \, 3)$.
#Toán lớp 10
2
NN
Nguyễn Nam Dương
10 tháng 2 2022

\(A=\left(m-2;6\right),B=\left(-2;2m+2\right).\)

Để \(A,B\ne\varnothing\)

\(\Rightarrow\orbr{\begin{cases}m-2\ge-2\\2m+2>6\end{cases}}\Rightarrow\orbr{\begin{cases}m\ge0\\m>2\end{cases}}\)

Kết hợp ĐK \(2< m< 8\)

\(\Rightarrow m\in\left(2;8\right)\)

Đúng(1)
DD
Đoàn Duy Nhật
10 tháng 2 2022
m€{2;8} nha HT @@@@@@@@@@
Đúng(0)
PT
Phạm Thị Mỹ Tình
8 tháng 8 2016
Hai bố con chạy tập thể dục trên một đường tròn của sân vận động. (xem hình vẽ). Bố chạy từ A. còn Con chạy từ B và ngược chiều nhau. A và B là hai điểm đối xứng qua tâm đường tròn. Nếu họ xuất phát cùng một lúc, gặp nhau lần đầu tiên sau khi Con đã đi được 100m và gặp nhau lần thứ 2 khi Bố còn 60m nữa thì hoàn tất 1 vòng. Hỏi chu vi vòng chạy là bao nhiêu?ai giải dc bài...
Đọc tiếp

Hai bố con chạy tập thể dục trên một đường tròn của sân vận động. (xem hình vẽ). Bố chạy từ A. còn Con chạy từ B và ngược chiều nhau. A và B là hai điểm đối xứng qua tâm đường tròn. Nếu họ xuất phát cùng một lúc, gặp nhau lần đầu tiên sau khi Con đã đi được 100m và gặp nhau lần thứ 2 khi Bố còn 60m nữa thì hoàn tất 1 vòng. Hỏi chu vi vòng chạy là bao nhiêu?

ai giải dc bài toán này là người giỏi nhất quả đất

giúp mk nhé mk tick cho
#Toán lớp 10
2
AI
Akita Izuki
8 tháng 8 2016

_ Khi gặp nhau lần thứ nhất thì hai bố con đã chạy được \(\frac{1}{2}\) vòng đua .

_ Khi gặp lần 2 thì 2 bố con đã chạy thêm được 1 vòng nữa .

_ Tổng số hai bố con đã chạy được : 1,5 vòng .

_Chỗ hai bố con gặp nhau con đã chạy quá nửa vòng là 60 mét .

Nửa chu vi đường chạy là :

        100 x ( 1,5 : 0,5 ) - 60 = 240 ( m )

Chu vi vòng chạy là : 

        240 x 2 = 480 ( m )

                    Đáp số : 480 m .

 
Đúng(0)
NT
Nguyễn Thị Khánh Linh
12 tháng 8 2016

Gọi nửa vòng tròn sân vận động là S, ta có lần gặp nhau đâu tiền hai bố con đã đi được quãng đường là S. Kể từ lần gặp đầu đến lần gặp thứ hai, cả hai bố con đi thêm được chu vi của đường tròn (tức là 2xS). Vậy lần gặp nhau thứ hai thì hai bố con đã đi được quãng đường là 3xS và thời gian gặp lần sau gấp 3 lần thời gian gặp lần đầu, Vậy suy ra lần gặp nhau thứ hai người con đã đi được quãng đường gấp 3 lần quãng đường lần gặp thứ nhất. 

Vậy quãng đường người con đã đi lần gặp thứ hai là:

S + 60 = 100 x 3

S + 60 = 300 (m)

S = 300 - 60

S = 240 (m)

Vậy chu vi vòng tròn là:

S x 2 = 240 x 2 

S x 2 = 480 (m)

Đáp số: 480m

tick nha Phạm Thị Mỹ Tình Phạm Thị Mỹ Tình

Đúng(0)
TQ
tao quen roi
19 tháng 5 2017
2 xe chuyển động ngược chiều hướng về nhau , vận tốc ban đầu của 2 xe là V1,V2(V1/V2=3/2) thời gian của từng xe lần lượt là T1 ,T2 (với T1,T2 là thời gian của V1,V2 ) với (T1,T2):(V1,V2) : khi V1 giảm 5/9 thì quang đường 2 xe đi được bằng nhau cũng trong lần gặp đầu tiên xe 1 hoàn thành 9/13 của quãng đường 260 _____________________________________________________ xét 2 xe đi chuyển trên khung đường...
Đọc tiếp

2 xe chuyển động ngược chiều hướng về nhau , vận tốc ban đầu của 2 xe là V1,V2(V1/V2=3/2)

thời gian của từng xe lần lượt là T1 ,T2 (với T1,T2 là thời gian của V1,V2 )

với (T1,T2):(V1,V2) : khi V1 giảm 5/9 thì quang đường 2 xe đi được bằng nhau

cũng trong lần gặp đầu tiên xe 1 hoàn thành 9/13 của quãng đường 260

_____________________________________________________

xét 2 xe đi chuyển trên khung đường hình chữ nhật

sau lần gặp thứ (1);(2);(3) vận tốc của mỗi xe sẽ tự tăng thêm 1/3 ( sau lần gặp (1) xe sẽ thay đổi vận tốc, sau lần gặp (2) xe sẽ thay đổi vận tốc , sau lần gặp (3)................(4)(ở lần này xe thay đổi vận tốc không như những lần (1);(2);(3)) .........)

sau lần gặp nhau thứ (4) xe sẽ giảm 29/50 vận tốc

tương tự : lần gặp nhau (5);(6);(7) giống như (1);(2);(3)>>>>>>>>>>>lần (8) =(4) (như một chu kì)

khung đường có dài =90 ,rộng =40

___________________________________________________________________________

với :trước khi vận tốc của xe 2 <5(**)

tính số lần 2 xe gặp nhau

tính tổng thời gian hai xe đi dược

tính quãng đường mỗi xe đi được

tính khoảng cách từ điểm xuất phát đến lần gặp nhau cuối xét ở trường hợp(**)
#Toán lớp 10
1
TQ
tao quen roi
20 tháng 5 2017

BS: với (T1,T2)(V1,V2) thì hai xe hoàn thành tổng quãng đường là 260

Đúng(0)
QT
Quoc Tran Anh Le
Giáo viên
1 tháng 10 2023

Trong một cuộc thi điền kinh gồm 6 vận động viên chạy trên 6 đường chạy. Hỏi có bao nhiêu cách xếp các vận động viên vào các đường chạy đó?
#Toán lớp 10
1
HQ
Hà Quang Minh
Giáo viên
1 tháng 10 2023

Số cách sắp xếp 6 vận động viên vào 6 đường chạy là số hoán vị của 6 phần tử.

=> Số cách xếp các vận động viên vào các đường chạy đó là:

  6! = 720 cách

Đúng(0)
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP