Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
\(y=x^4+2(m-4)x^2+m+5\)
\(\Rightarrow y'=4x^3+4(m-4)x\)
\(y'=0\Leftrightarrow x(x^2+m-4)=0\Leftrightarrow \left[\begin{matrix} x=0\\ x^2=4-m\end{matrix}\right.\)
Để đths có 3 điểm cực trị thì \(y'=0\) phải có ít nhất 3 nghiệm pb. Khi đó \(4-m>0\Rightarrow m< 4\)
Khi đó, các điểm cực trị là:
\((0; m+5)\)
\((\sqrt{4-m}, -m^2+9m-11)\)
\((-\sqrt{4-m}, -m^2+9m-11)\)
Nếu $O$ là trọng tâm:
\(\left\{\begin{matrix} \frac{0+\sqrt{4-m}-\sqrt{4-m}}{3}=x_O=0\\ \frac{m+5+2(-m^2+9m-11)}{3}=y_O=0\end{matrix}\right.\)
\(\Leftrightarrow -2m^2+19m-17=0\Rightarrow \left[\begin{matrix} m=\frac{17}{2}\\ m=1\end{matrix}\right.\)
Vì $m< 4$ nên $m=1$
Bài 2:
\(y'=4x^3-4mx=0\Leftrightarrow \left[\begin{matrix}
x=0\\
x^2=m\end{matrix}\right.\)
Để hàm bậc 4 có 3 cực trị thì $y'=0$ phải có 3 nghiệm pb, suy ra $m>0$
Khi đó: \(y'=0\Leftrightarrow \left[\begin{matrix} x=0\\ x=\sqrt{m}\\ x=-\sqrt{m}\end{matrix}\right.\)
Ba điểm cực trị:
\(A(0; m-1)\)
\(B(\sqrt{m}; -m^2+m-1)\)
\(C(-\sqrt{m}; -m^2+m-1)\)
Suy ra:
\(\overrightarrow{BC}=(-2\sqrt{m};0)\); \(\overrightarrow{AB}=(\sqrt{m}; -m^2)\)
\(\overrightarrow{OA}=(0;m-1)\); \(\overrightarrow{OC}=(-\sqrt{m}; -m^2+m-1)\)
Vì $O$ là trực tâm nên : \(\left\{\begin{matrix} \overrightarrow{BC}.\overrightarrow{OA}=0\\ \overrightarrow{AB}.\overrightarrow{OC}=0\end{matrix}\right.\)
\(\Rightarrow \left\{\begin{matrix} -2\sqrt{m}.0+0.(m-1)=0\\ -m+m^2(m^2-m+1)=0\end{matrix}\right.\)
\(\Rightarrow m(m^3-m^2+m-1)=0\)
\(\Leftrightarrow m(m^2+1)(m-1)=0\Rightarrow m=1\) vì \(m>0\)
Vậy.......

a) Xét hàm số \(y=ax^4+bx^2+c\)
Ta có \(y'=4ax^3+2bx=2x\left(2ax^2+b\right)\)
\(y'=0\Leftrightarrow x=0\) hoặc \(2ax^2+b=0\left(1\right)\)
Đồ thị hàm số có 3 cực trị phân biệt khi và chỉ khi \(y'=0\) có 3 nghiệm phân biệt hay phương trình (1) có 2 nghiệm phân biệt khác 0 \(\Leftrightarrow ab< 0\) (*)
Với điều kiện (*) thì đồ thị có 3 điểm cực trị là :
\(A\left(0;c\right);B\left(-\sqrt{-\frac{b}{2a},}c-\frac{b^2}{4a}\right);C\left(\sqrt{-\frac{b}{2a},}c-\frac{b^2}{4a}\right)\)
Ta có \(AB=AC=\sqrt{\frac{b^2-8ab}{16a^2}};BC=\sqrt{-\frac{2b}{a}}\) nên tam giác ABC vuông khi và chỉ khi vuông tại A.
Khi đó \(BC^2=2AB^2\Leftrightarrow b^3+8a=0\)
Do đó yêu cầu bài toán\(\Leftrightarrow\begin{cases}ab< 0\\b^3+8a=0\end{cases}\)\(\Leftrightarrow\begin{cases}-2\left(m+1\right)< 0\\-8\left(m+1\right)^3+8=0\end{cases}\)\(\Leftrightarrow m=0\)
b) Ta có yêu cầu bài toán \(\Leftrightarrow\begin{cases}ab< 0\\OA=BC\end{cases}\)\(\Leftrightarrow\begin{cases}-2\left(m+1\right)< 0\\m^2-4\left(m+1\right)=0\end{cases}\)
\(\Leftrightarrow m=2\pm2\sqrt{2}\)

Chọn D
Phương trình hoành độ giao điểm :
![]()
Theo yêu cầu bài toán : ![]() phải có hai nghiệm phân biệt khác
phải có hai nghiệm phân biệt khác ![]()
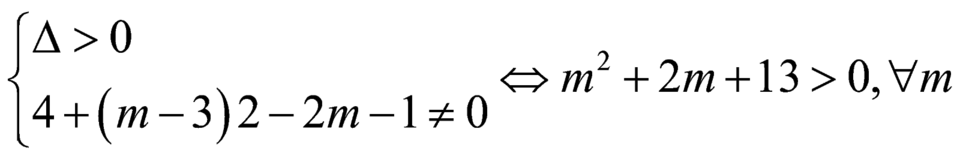
Gọi ![]() ,
,![]() suy ra
suy ra ![]() là trọng tâm của tam giác
là trọng tâm của tam giác ![]() :
:
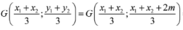
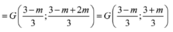
Theo yêu cầu bài toán :
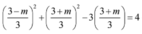
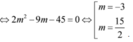 .
.

Phương trình hoành độ giao điểm \(3x^2+2mx+3m-4=0\left(1\right)\) với x. Đường thẳng d cắt đồ thị (C) tại hai điểm phân biệt khi và chỉ khi phương trình (1) có 2 nghiệm phân biệt khác -1
\(\Leftrightarrow\begin{cases}9m^2-36m+48>0\\0.m-1\ne0\end{cases}\) (đúng với mọi m)
Gọi \(x_1;x_2\) là các nghiệm của phương trình (1), ta có : \(\begin{cases}x_1+x_2=-m\\x_1x_2=\frac{3m-4}{3}\end{cases}\) (*)
Giả sử \(A\left(x_1;x_1+m\right);B\left(x_2;x_2+m\right)\)
Khi đó ta có \(OA=\sqrt{x^2_1+\left(x_1+m\right)^2};OA=\sqrt{x^2_2+\left(x_2+m\right)^2}\)
Kết hợp (*) ta được \(OA=OB=\sqrt{x_1^2+x_2^2}\)
Suy ra tam giác OAB cân tại O
Ta có \(AB=\sqrt{2\left(x_1-x_2\right)^2}\). Tam giác OAB đều \(\Leftrightarrow OA^2=AB^2\Leftrightarrow x_1^2+x_2^2=2\left(x_1-x_2\right)^2\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-6x_1x_2=0\)
\(\Leftrightarrow m^2-6m+8=0\Leftrightarrow m=2\) hoặc m=4

Câu 1:
Để dễ nhìn hơn, ta đặt \(log_2m=a\) phương trình trở thành:
\(3^{3a}-3^{-3a}+3^{a^2+2}-3^{-a^2-2}=0\)
\(\Leftrightarrow3^{3a}-3^{-3a}=3^{-a^2-2}-3^{-\left(-a^2-2\right)}\) (1)
Xét hàm \(f\left(t\right)=3^t-3^{-t}\Rightarrow f'\left(t\right)=3^t.ln3+3^{-t}.ln3>0\)
\(\Rightarrow f\left(t\right)\) đồng biến \(\Rightarrow\left(1\right)\) xảy ra khi và chỉ khi \(3a=-a^2-2\)
\(\Leftrightarrow a^2+3a+2=0\Leftrightarrow\left[{}\begin{matrix}a=-1\\a=-2\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}log_2m=-1\\log_2m=-2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}m=\frac{1}{2}\\m=\frac{1}{4}\end{matrix}\right.\) \(\Rightarrow T=\frac{1}{8}\)
Câu 2:
\(x_M=1\Rightarrow y_M=-3m^2+2m+6\)
\(y'=-3x^2+4\left(m+1\right)x-3m^2+3\)
\(\Rightarrow y'\left(1\right)=-3m^2+4m+4\)
Phương trình tiếp tuyến tại M:
\(y=\left(-3m^2+4m+4\right)\left(x-1\right)-3m^2+2m+6\)
\(\Leftrightarrow y=\left(-3m^2+4m+4\right)x-2m+2\)
Để tiếp tuyến song song với d: \(\left\{{}\begin{matrix}-3m^2+4m+4=-3\\-2m+2\ne4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3m^2-4m-7=0\\m\ne-1\end{matrix}\right.\) \(\Rightarrow m=\frac{7}{3}\Rightarrow\) có đúng 1 giá trị m thỏa mãn
Câu 3:
Áp dụng điều kiện của nghiệm của pt lượng giác bậc nhất:
\(1^2+\left(m-1\right)^2\ge\left(2m-1\right)^2\)
\(\Leftrightarrow m^2-2m+2\ge4m^2-4m+1\)
\(\Leftrightarrow3m^2-2m-1\le0\)
\(\Rightarrow\frac{-1}{3}\le m\le1\Rightarrow m=\left\{0;1\right\}\) có 2 giá trị nguyên
Câu 4:
Sao lại là \(\left|1z-2-i\right|\), sự xuất hiện số 1 bất thường làm mình nghĩ bạn gõ nhầm chỗ nào đó, nhưng thực ra chỉ cần phương pháp giải, còn số liệu thì chỉ việc thay đổi thôi
Với dữ kiện để bài, ta thấy ngay tập hợp \(z\) là các điểm \(M\left(x;y\right)\) nằm trên đường tròn \(\left(x-2\right)^2+\left(y-1\right)^2=9\)
Gọi \(A\left(4;1\right)\) và \(B\left(-5;-8\right)\)
\(\Rightarrow P=\left|z-4-i\right|+\left|z+5+8i\right|=MA+MB\)
Bài toán quy về tìm điểm M thuộc đường tròn cố định và 2 điểm A, B cố định sao cho \(MA+MB\) đạt max
Gọi H là trung điểm AB \(\Rightarrow H\left(-\frac{1}{2};-\frac{7}{2}\right)\)
Áp dụng BĐT Bunhiacôpxki ta có:
\(P=MA+MB\le\sqrt{2\left(MA^2+MB^2\right)}\)
Theo công thức trung tuyến trong tam giác MAB ta có:
\(MA^2+MB^2=2MH^2+\frac{AB^2}{2}\)
\(\Rightarrow P\le\sqrt{2\left(MH^2+\frac{AB^2}{2}\right)}\) (1)
AB cố định \(\Rightarrow P_{max}\) khi \(MH_{max}\Rightarrow M\) là giao điểm nằm khác phía H so với I của đường thẳng IH và đường tròn (C)
\(\overrightarrow{BA}=\left(9;9\right)=9\left(1;1\right)\Rightarrow\)phương trình đường thẳng IH:
\(x+\frac{1}{2}+y+\frac{7}{2}=0\Leftrightarrow x+y+4=0\)
Tọa độ M: \(\left\{{}\begin{matrix}\left(x-2\right)^2+\left(y-1\right)^2=9\\x+y+4=0\end{matrix}\right.\)
Số xấu, nghĩa là linh cảm đúng, pt ban đầu bạn viết nhầm :(
Đến đây chỉ việc giải ra tọa độ M, sau đó thay vào công thức (1) là xong

Chọn C
![]() .
.
Vì ![]() nên phương trình
nên phương trình ![]() có 2 nghiệm phân biệt.
có 2 nghiệm phân biệt.
Do đó hàm số có hai điểm cực trị ![]() .
.
Giả sử hàm số có hai điểm cực trị lần lượt là ![]() và
và ![]() , với
, với ![]() ,
, ![]() là nghiệm của phương trình
là nghiệm của phương trình ![]() .
.
Thực hiện phép chia ![]() cho
cho ![]() ta được :
ta được : ![]() .
.
Khi đó ta có: 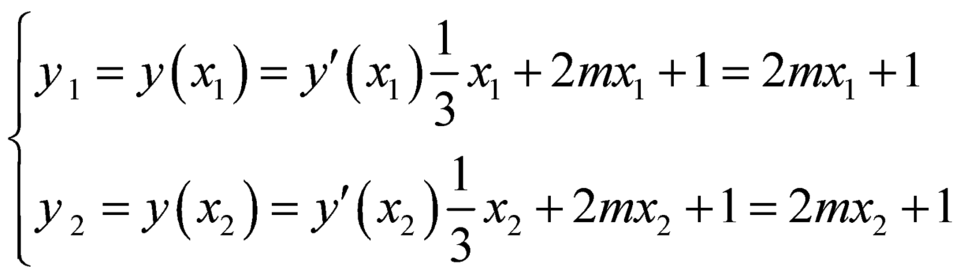 .
.
Ta thấy, toạ độ hai điểm ![]() và
và ![]() thoả mãn phương trình
thoả mãn phương trình ![]() .
.
Do đó, phương trình đường thẳng qua hai điểm cực trị là ![]() .
.
Ta thấy ![]() luôn qua
luôn qua ![]() .
.
Đặt ![]()
![]() .
.
![]() .
.
Xét hàm số ![]() ,
, ![]() .
.
![]() ,
, ![]() .
.
Suy ra hàm số ![]() liên tục và đồng biến trên
liên tục và đồng biến trên ![]() .
.
Do đó ![]() .
.
Vậy ![]() đạt giá trị lớn nhất
đạt giá trị lớn nhất ![]()
![]() .
.


Đầu tiên, ta cần tìm điểm cực trị của hàm số f(x) = x^3 - 3x^2 + m. Điều kiện cần và đủ để x_0 là điểm cực trị của hàm số y = f(x) là f’(x_0) = 0 và f’'(x_0) ≠ 0.
Ta có f’(x) = 3x^2 - 6x và f’'(x) = 6x - 6.
Giải phương trình f’(x) = 0, ta được x_1 = 0 và x_2 = 2. Kiểm tra điều kiện thứ hai, ta thấy f’‘(0) = -6 ≠ 0 và f’'(2) = 6 ≠ 0 nên x_1 = 0 và x_2 = 2 là hai điểm cực trị của hàm số.
Vậy, A = (0, f(0)) = (0, m) và B = (2, f(2)) = (2, 4 - m).
Trọng tâm G của tam giác OAB có tọa độ (x_G, y_G) = (1/3 * (x_A + x_B + x_O), 1/3 * (y_A + y_B + y_O)) = (2/3, 1/3 * (m + 4)).
Để G thuộc đường thẳng 3x + 3y - 8 = 0, ta cần có 3 * (2/3) + 3 * (1/3 * (m + 4)) - 8 = 0. Giải phương trình này, ta được m = 2.
Vậy, đáp án là B. m = 2.