K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
ND
3
TA
2 tháng 8 2021
\(\left\{{}\begin{matrix}16-x^2\ge0\\2x+1>0\\x^2-8x+14\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-4\le x\le4\\x>-\dfrac{1}{2}\\\left[{}\begin{matrix}x\ge4+\sqrt{2}\\x\le4-\sqrt{2}\end{matrix}\right.\end{matrix}\right.\Leftrightarrow-\dfrac{1}{2}< x\le4-\sqrt{2}\)
2 tháng 8 2021
xác định \(< =>\left\{{}\begin{matrix}\sqrt{16-x^2}\ge0\\\sqrt{2x+1}>0\\\sqrt{x^2-8x+14}\ge0\end{matrix}\right.\)
\(< =>\left\{{}\begin{matrix}-4\le x\le4\\x>-\dfrac{1}{2}\\\left[{}\begin{matrix}x\le4-\sqrt{2}\\x\ge4_{ }+\sqrt{2}\end{matrix}\right.\\\end{matrix}\right.\)\(< =>-\dfrac{1}{2}< x\le4-\sqrt{2}\)
KV
29 tháng 10 2023
ĐKXĐ:
1 - x² ≥ 0 và x - 1 ≥ 0
⇔ x² ≤ 1 và x ≥ 1
⇔ -1 ≤ x ≤ 1 và x ≥ 1
⇔ x = 1
NK
1
KK
13 tháng 9 2021
a. không có ĐK, vì muốn a đc xác định cần \(\sqrt{x-9}\) và \(\sqrt{6-x}\) \(\ge0\)
mà điều kiện để \(\sqrt{x-9}\) và \(\sqrt{6-x}\ge0\) là \(9\le x\le6\)
Dễ thấy không có số nào tương thích với x
TP
21 tháng 6 2019
\(B=\frac{9-x}{\sqrt{x}+3}-\frac{x-6\sqrt{x}+9}{\sqrt{x}-3}-6\)(đk: x ≥ 0 và x ≠ 9)
\(B=\frac{\left(3-\sqrt{x}\right)\left(3+\sqrt{x}\right)}{\sqrt{x}+3}-\frac{\left(\sqrt{x}-3\right)^2}{\sqrt{x}-3}-6\)
\(B=\left(3-\sqrt{x}\right)-\left(\sqrt{x}-3\right)-6\)
\(B=3-\sqrt{x}-\sqrt{x}+3-6\)
\(B=-2\sqrt{x}\)
TP
21 tháng 6 2019
\(A=\frac{\sqrt{x}}{\sqrt{x}-6}-\frac{3}{\sqrt{x}+6}+\frac{x}{36-x}\)(đk: x ≥ 0 và x ≠ 36)
\(=\frac{\sqrt{x}}{\sqrt{x}-6}-\frac{3}{\sqrt{x}+6}-\frac{x}{x-36}\)
\(=\frac{\sqrt{x}}{\sqrt{x}-6}-\frac{3}{\sqrt{x}+6}-\frac{x}{x-36}\)
\(=\frac{\sqrt{x}\left(\sqrt{x}+6\right)-3\left(\sqrt{x-6}\right)-x}{(\sqrt{x}-6)\left(\sqrt{x}+6\right)}\)
\(=\frac{x+6\sqrt{x}-3\sqrt{x}+18-x}{(\sqrt{x}-6)\left(\sqrt{x}+6\right)}\)
\(=\frac{3\sqrt{x}+18}{(\sqrt{x}-6)\left(\sqrt{x}+6\right)}\)
\(=\frac{3(\sqrt{x}+6)}{(\sqrt{x}-6)\left(\sqrt{x}+6\right)}\)
\(=\frac{3}{\sqrt{x}-6}\)
6 tháng 9 2017
\(\frac{\sqrt{x}}{\sqrt{x}-1}-\frac{2\sqrt{x}-1}{\sqrt{x}\left(\sqrt{x}-1\right)}=\frac{x-2\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}=\frac{\sqrt{x}-1}{\sqrt{x}}\)
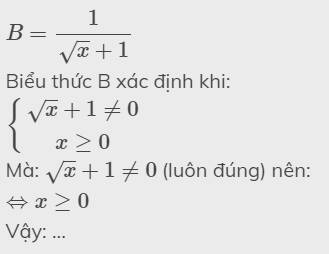
\(DK:\left\{{}\begin{matrix}x\ge0\\\sqrt{x}+1\ne0\end{matrix}\right.\)
\(< =>\left\{{}\begin{matrix}x\ge0\\\sqrt{x}\ne-1\end{matrix}\right.\)
\(< =>x\ge0\) ( Vì : \(\forall x\ge0=>\sqrt{x}\ge0\) )
\(B=\dfrac{1}{\sqrt{x}+1}\)
Biểu thức B xác định khi:
\(\left\{{}\begin{matrix}\sqrt{x}+1\ne0\\x\ge0\end{matrix}\right.\)
Mà: \(\sqrt{x}+1\ne0\) (luôn đúng) nên:
\(\Leftrightarrow x\ge0\)
Vậy: ...