K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
BC
1
L
18 tháng 2 2016
a) \(6x-35+5x-21=17x-20\)
\(\Rightarrow6x-25+5x-21+20=17x\)
\(\left(6x+5x\right)+\left(20-25-21\right)=17x\)
\(11x+\left(-36\right)=17x\)
\(17x-11x=-36\)
\(6x=-36\)
\(x=\frac{-36}{6}=-6\)
Vậy \(x=-6\)
b) \(5x+35-4x-27=14x+34\)
\(\Rightarrow5x+35-4x-27-34=14x\)
\(\left(5x-4x\right)+\left(35-27-34\right)=14x\)
\(x+\left(-26\right)=14x\)
\(14x-x=-26\)
\(13x=-26\)
\(x=-\frac{26}{13}=-2\)
Vậy \(x=-2\)
21 tháng 7 2016
16 = 13 + 3^1
22 = 16 + 6^1
26 = 22 + 2^2
62 = 26 + 6^2
=> 62 + 2^6 = 126
22 tháng 4 2016
6./x-7/-26=-7
6./x-7/ =-7+26
6./x-7/ =19
/x-7/ =19:6
/x-7/ =19/6
x-7=19/6 hoặc x-7=-19/6
=>x=61/6 hoặc x=23/6
18 tháng 4 2016
Đường thẳng d qua điểm M(1 ; 2 ; 0) và có vec tơ chỉ phương (-1 ; 2 ; 3).
Đường thẳng d' qua điểm M'(1 ; 3 ;1) và có vectơ chỉ phương (1 ; -2 ; 0).
Cách 1. Xét
= (2 ; 1 ;-5).
= (0 ; 1 ; 1).
Ta có : = 2.0 + 1.1 + (-5).1 = -4 ≠ 0.
Do đó d và d' chéo nhau.
Cách 2: Vì và
không cùng phương nên d và d' chỉ có thể là chéo nhau hoặc cắt nhau.
Ta xét giao điểm của d và d':
=>
hệ vô nghiệm.
Do đó d và d' không thể cắt nhau. Vì vậy d và d' chéo nhau.
18 tháng 4 2016
a) Thay các tọa độ x ; y ; z trong phương trình tham số của d vào phương trình (α) ta có:
3(12 + 4t) +5(9 + 3t) - (1 + t) = 0
⇔ 26t + 78 = 0 ⇔ t = -3.
Tức là d ∩ (α) = M(0 ; 0 ; -2).
Trong trường hợp này d cắt (α) tại điểm M.
b) Thay các tọa độ x ; y ; z trong phương trình tham số của d vào phương trình (α) ta có:
(1 + t) + 3.(2 - t) + (1 + 2t) + 1 = 0
⇔ 0.t + t = 9, phương trình vô nghiệm.
Chứng tỏ d và (α) không cắt nhau., ta có d // (α).
c) Thay các tọa độ x ; y ; z trong phương trình tham số của d vào phương trình (α) ta có:
(1 + 1) + (1+ 2t) + (2 - 3t) - 4 = 0
⇔ 0t + 0 = 0,phương trình này có vô số nghiệm, chứng tỏ d ⊂ (α) .
19 tháng 3 2016
a) Thay các tọa độ x ; y ; z trong phương trình tham số của d vào phương trình (α) ta có:
3(12 + 4t) +5(9 + 3t) - (1 + t) = 0
⇔ 26t + 78 = 0 ⇔ t = -3.
Tức là d ∩ (α) = M(0 ; 0 ; -2).
Trong trường hợp này d cắt (α) tại điểm M.
b) Thay các tọa độ x ; y ; z trong phương trình tham số của d vào phương trình (α) ta có:
(1 + t) + 3.(2 - t) + (1 + 2t) + 1 = 0
⇔ 0.t + t = 9, phương trình vô nghiệm.
Chứng tỏ d và (α) không cắt nhau., ta có d // (α).
c) Thay các tọa độ x ; y ; z trong phương trình tham số của d vào phương trình (α) ta có:
(1 + 1) + (1+ 2t) + (2 - 3t) - 4 = 0
⇔ 0t + 0 = 0,phương trình này có vô số nghiệm, chứng tỏ d ⊂ (α) .
19 tháng 3 2016
Xét hệ
Hai đường thẳng d và d' cắt nhau khi và chỉ khi hệ có nghiệm duy nhất.
Nhân hai về của phương trình (3) với 2 rồi cộng vế với vế vào phương trình (2), ta có t = 2;
s = 0. Thay vào phương trình (1) ta có 1 + 2a = 1 => a =0.
Vậy a = 0 thì d và d' cắt nhau.
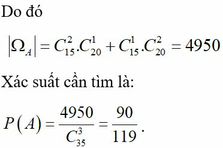
61
61