Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Doanh thu khi bán Q sản phẩm là 170Q nghìn đồng.
Lợi nhuận khi bán Q sản phẩm là \(170Q - \left( {{Q^2} + 30Q + 3300} \right)\)\( = - {Q^2} + 140Q - 3300\)(nghìn đồng)
Để không bị lỗ thì \( - {Q^2} + 140Q - 3300 \ge 0\left( 1 \right)\)
\(a = - 1 < 0;\Delta ' = 1600\)
\( - {Q^2} + 140Q - 3300 = 0\) có 2 nghiệm phân biệt \({x_1} = 30,{x_2} = 110\)
(1)\( \Leftrightarrow \)\(30 \le x \le 110\)
Vậy để không bị lỗ thì số sản phẩm được sản suất phải nằm trong khoảng từ 30 đến 110 sản phẩm.

Gọi x là số đơn vị sản phẩm loại I, y là số đơn vị sản phẩm loại II sản xuất ra.
Như vậy tiền lãi có được là L = 3x + 5y (nghìn đồng).
Theo đề bài: Nhóm A cần 2x + 2y máy;
Nhóm B cần 0x + 2y máy;
Nhóm C cần 2x + 4y máy;
Vì số máy tối đa ở nhóm A là 10 máy, nhóm B là 4 máy, nhóm C là 12 máy nên x, y phải thỏa mãn hệ bất phương trình: 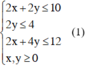
Khi đó bài toán trở thành: trong các nghiệm của hệ bất phương trình (1) thì nghiệm (x = xo; y = yo) nào cho L = 3x + 5y lớn nhất.
Miền nghiệm của hệ bất phương trình (1) là ngũ giác ABCDE kể cả miền trong.
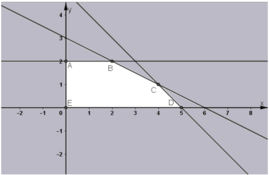
Ta có: L đạt giá trị lớn nhất tại một trong các đỉnh của ngũ giác ABCDE.
Tính giá trị của biểu thức L = 3x + 5y tại các đỉnh ta được:
Tại đỉnh A(0;2), L = 10
Tại đỉnh B(2; 2), L = 16
Tại đỉnh C(4; 1), L = 17
Tại đỉnh D(5; 0), L = 15
Tại đỉnh E(0; 0), L = 0.
Do đó, L = 3x + 5y lớn nhất là 17 (nghìn đồng) khi: x = 4; y = 1
Vậy để có tiền lãi cao nhất, cần sản xuất 4 đơn vị sản phẩm loại I và 1 đơn vị sản phẩm loại II.

Gọi x là số đơn vị sản phẩm loại I, y là số đơn vị sản phẩm loại II được nhà máy lập kế hoạch sản xuất. Khi đó số lãi nhà máy nhân được là P = 3x + 5y (nghìn đồng).
Các đại lượng x, y phải thỏa mãn các điều kiện sau:
(I)
(II)
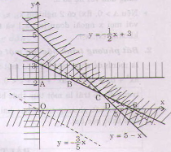
Miền nghiệm của hệ bất phương trình (II) là đa giác OABCD (kể cả biên).
Biểu thức F = 3x + 5y đạt giá trị lớn nhất khi (x; y) là tọa độ đỉnh C.
(Từ 3x + 5y = 0 => y = Các đường thẳng qua các đỉnh của OABCD và song song với đường y =
cát Oy tại điểm có tung độ lớn nhất là đường thẳng qua đỉnh C).
Phương trình hoành độ điểm C: 5 - x = <=> x = 4.
Suy ra tung độ điểm C là yc = 5 - 4 = 1. Tọa độ C(4; 1). Vậy trong các điều kiện cho phép của nhà máy, nếu sản xuất 4 đơn vị sản phẩm loại I và 1 đơn vị sản phẩm đơn vị loại II thì tổng số tiền lãi lớn nhất bằng:
Fc = 3.4 + 5.1 = 17 nghìn đồng.

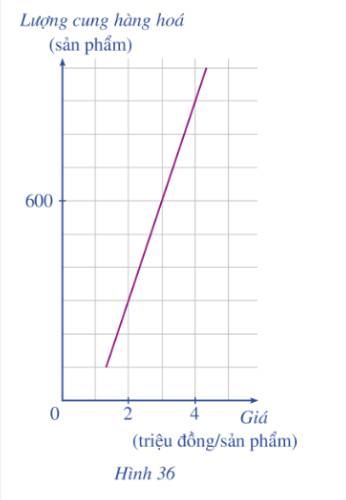
a) Từ đồ thị ta thấy khi giá bán là 2 triệu đồng/sản phẩm thì lượng cung hàng hóa là: 300 sản phẩm, khi giá bán là 4 triệu đồng/sản phẩm thì lượng cung hàng hóa là 900 sản phẩm.
b) Khi nhu cầu thị trường là 600 sản phẩm, để cân bằng thị trường thì lượng cung bằng lượng cầu. Khi đó lượng cung hàng hóa cũng là 600 sản phẩm.
Từ đồ thị ta thấy khi lượng cung hàng hóa là 600 sản phẩm thì giá bán là 3 triệu đồng/sản phẩm.

a) Doanh thu khi bán hết Q sản phẩm là 1200Q (nghìn đồng)
Lợi nhuận bán hết Q sản phẩm là:
\(\begin{array}{l}1200Q - \left( {{Q^2} + 180Q + 140000} \right)\\ = - {Q^2} + 1020Q - 140000\end{array}\)
b)
Để xí nghiệp hòa vốn thì: Lợi nhuận bằng 0.
\(\begin{array}{l} \Leftrightarrow - {Q^2} + 1020Q - 140000 = 0\\ \Leftrightarrow \left[ \begin{array}{l}Q \approx 857\\Q \approx 163\end{array} \right.\end{array}\)
Vậy xí nghiệp sản xuất 163 sản phẩm hoặc 857 sản phẩm thì hòa vốn.
c) Để không bị lỗ thì lợi nhuận lớn hơn hoặc bằng 0.
Khi đó:
\(\begin{array}{l} - {Q^2} + 1020Q - 140000 \ge 0\\ \Leftrightarrow 163,45 \le Q \le 857,55\\ \Rightarrow 164 \le Q \le 857\end{array}\)
Vậy để không bị lỗ thì xí nghiệp cần sản xuất số sản phẩm nằm trong khoảng 164 đến 857.

a) Thay x=100 ta được:
\(y = - {200.100^2} + 92000.100 - 8400000\)
\( = - 1200000\)
Thay x=200 ta được:
\(\begin{array}{l}y = - {200.200^2} + 92000.200 - 8400000\\ = 2000000\end{array}\)
Vậy với \(x = 100\) thì \(y = - 1200000\)
Với \(x = 200\) thì \(y = 2000000\)
b) Với mỗi giá trị của x có 1 giá trị tương ứng của y.

Tham khảo:
Gọi x, y lần lượt là số tấn sản phẩm X, Y mà xưởng cần sản xuất mỗi ngày.
Ta có các điều kiện ràng buộc đối với x, y như sau:
- Hiển nhiên \(x \ge 0,y \ge 0\)
- Máy A làm việc không quá 12 giờ một ngày nên \(6x + 2y \le 12\)
- Máy B làm việc không quá 8 giờ một ngày nên \(2x + 2y \le 8\)
Từ đó ta có hệ bất phương trình:
\(\left\{ \begin{array}{l}6x + 2y \le 12\\2x + 2y \le 8\\x \ge 0\\y \ge 0\end{array} \right.\)
Biểu diễn từng miền nghiệm của mỗi bất phương trình trên hệ trục tọa độ Oxy.
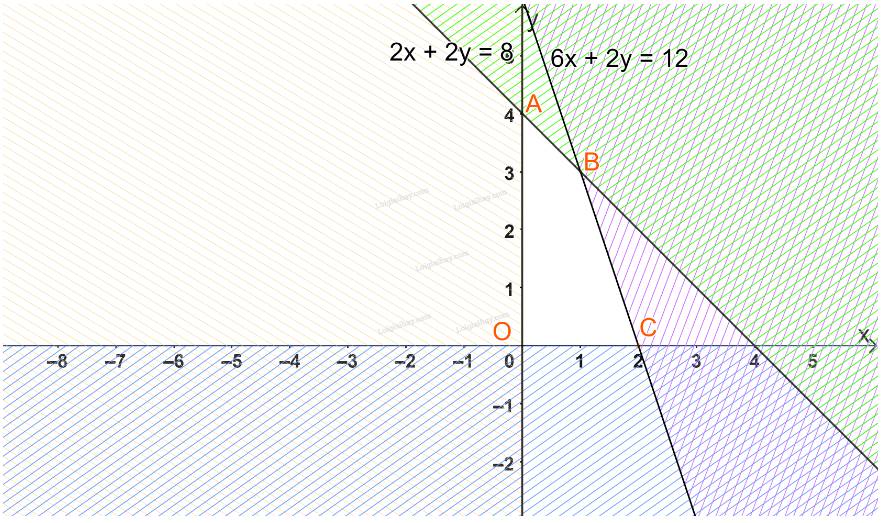
Miền không gạch chéo (miền tứ giác OABC, bao gồm cả các cạnh) trong hình trên là phần giao của các miền nghiệm và cũng là phần biểu diễn nghiệm của hệ bất phương trình đã cho.
Với các đỉnh \(O(0;0),A(0;4),\)\(B(1;3),\)\(C(2;0).\)
Gọi F là số tiền lãi (đơn vị: triệu đồng) thu về, ta có: \(F = 10x + 8y\)
Tính giá trị của F tại các đỉnh của tứ giác:
Tại \(O(0;0),\)\(F = 10.0 + 8.0 = 0\)
Tại \(A(0;4):\)\(F = 10.0 + 8.4 = 32\)
Tại \(B(1;3),\)\(F = 10.1 + 8.3 = 34\)
Tại \(C(2;0).\)\(F = 10.2 + 8.0 = 20\)
F đạt giá trị lớn nhất bằng \(34\) tại \(B(1;3).\)
Vậy xưởng đó nên sản xuất 1 tấn sản phầm loại X và 3 tấn sản phầm loại Y để tổng số tiền lãi là lớn nhất.

Theo đề bài, giá bán \(x\) sản phẩm là \(170x\) (nghìn đồng)
Để nhà sản xuất không bị lỗ thì \(P\left(x\right)\le170x\) \(\Leftrightarrow x^2+30x+3300\le170x\) \(\Leftrightarrow x^2-140x+3300\le0\) \(\Leftrightarrow\left(x-110\right)\left(x-30\right)\le0\)
Đặt \(f\left(x\right)=\left(x-110\right)\left(x-30\right)\). Ta lập bảng xét dấu:
Vậy \(f\left(x\right)\le0\Leftrightarrow x\in\left[30;110\right]\). Do đó, để nhà sản xuất không bị lỗ thì số sản phẩm được sản xuất trong đoạn \(\left[30;110\right]\).
Khi bán hết �x sản phẩm thì số tiền thu được là: 170�170x (nghìn đồng).
Điều kiện để nhà sản xuất không bị lỗ là 170�≥�2+30�+3300⇔�2−140�+3300≤0170x≥x2+30x+3300⇔x2−140x+3300≤0.
Xét �2−140�+3300=0⇒�=30x2−140x+3300=0⇒x=30 hoặc �=110x=110.
Bảng xét dấu �(�)=�2−140�+3300f(x)=x2−140x+3300:
∞!aaaaa + ∞ − + ∞ − xf(x)00 + 30110
Ta có: �2−140�+3300≤0⇔�∈[30;110]x2−140x+3300≤0⇔x∈[30;110].
Vậy nếu nhà sản xuất làm ra từ 3030 đến 110110 sản phẩm thì họ sẽ không bị lỗ.