Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

3, Áp dụng BĐT Cauchy Schwarz dạng cộng mẫu thức ta có :
\(x^2+y^2\ge\frac{\left(x+y\right)^2}{2}=2\)
Đẳng thức xảy ra khi và chỉ khi \(x=y=1\)
Vậy ta có điều phải chứng minh
2 b
\(bđt< =>a^2c^2+b^2d^2+2abcd\le a^2c^2+a^2d^2+b^2c^2+b^2d^2\)
\(< =>2abcd\le a^2d^2+b^2c^2\)
\(< =>a^2b^2+b^2c^2-2abcd\ge0\)
\(< =>\left(ab-cd\right)^2\ge0\)*đúng*
Dấu "=" xảy ra khi và chỉ khi \(\frac{a}{b}=\frac{c}{d}\)
Vậy ta đã hoàn tất chứng minh

\(\Delta=\left(2m-1\right)^2+4m=4m^2+1>0,\forall m\)
=> Phương trình có 2 nghiệm phân biệt
Áp dụng định lí viet ta có: \(x_1+x_2=-\left(2m-1\right);x_1.x_2=-m\)
Ta có: \(A=x_1^2+x_2^2-x_1x_2=\left(x_1+x_2\right)^2-3x_1x_2\)
\(=\left(2m-1\right)^2+3m=4m^2-m+1\)
\(=\left(2m\right)^2-2.2m.\frac{1}{4}+\frac{1}{16}-\frac{1}{16}+1\)
\(=\left(2m-\frac{1}{4}\right)^2+\frac{15}{16}\ge\frac{15}{16}\)
Dấu "=" xảy ra <=> m = 1/8
Vậy min A = 15/16 khi m = 1/8
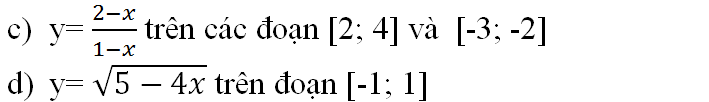
a)
\(x=-2\) là nghiệm của phương trình
\(\Rightarrow\left(-2\right)^2-\left(-2\right).\left(m-1\right).\left(-2\right)-3=0\)
\(\Leftrightarrow4+4\left(m-1\right)-3=0\)
\(\Leftrightarrow4\left(m-1\right)=-1\)
\(\Leftrightarrow m-1=-\dfrac{1}{4}\)
\(\Leftrightarrow m=\dfrac{3}{4}\)
\(x^2-2\left(m-1\right)x-3=0\)
\(\Leftrightarrow x^2+\dfrac{1}{2}x-3=0\)
\(\Leftrightarrow2x^2+x-6=0\)
\(\Leftrightarrow\left(x+2\right)\left(2x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+2=0\\2x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=\dfrac{3}{2}\end{matrix}\right.\)
b)
\(\Delta'=\left(m-1\right)^2+12x>0\forall m\)
\(\Rightarrow\) Phương trình luôn có 2 nghiệm phân biệt
Theo Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1x_2=-3\end{matrix}\right.\)
Có:
\(Q=x_1^3x_2+x_1x_2^3-5x_1x_2\)
\(=x_1x_2.\left[\left(x_1+x_2\right)^2-2x_1x_2\right]-5x_1x_2\)
\(=-3\left[4\left(m-1\right)^2+6\right]+15\)
\(=-12\left(m-1\right)^2-3\)
Mà \(-12\left(m-1\right)^2\le0\)
\(\Rightarrow-12\left(m-1\right)^2-3\le-3\)
\(Max_Q=-3\Leftrightarrow m-1=0\Leftrightarrow m=1\).
`a)` Thay `x=-2` vào ptr có:
`(-2)^2-2(m-1).(-2)-3=0<=>m=3/4`
Thay `m=3/4` vào ptr có: `x^2-2(3/4-1)x-3=0<=>x^2+1/2x-3=0`
`<=>2x^2+x-6=0<=>(x+2)(2x-3)=0<=>[(x=-2),(x=3/2):}`
`b)` Ptr có nghiệm `<=>\Delta' >= 0`
`<=>[-(m-1)]^2+3 >= 0<=>(m-1)^2+3 >= 0` (LĐ `AA m`)
`=>` Áp dụng Viét có: `{(x_1+x_2=[-b]/a=2m-2),(x_1 .x_2=c/a=-3):}`
Có:`Q=x_1 ^3 x_2+x_1 x_2 ^3 -5x_1 x_2`
`<=>Q=x_1 x_2(x_1 ^2+x_2 ^2)-5x_1 x_2`
`<=>Q=x_1 x_2[(x_1+x_2)^2-2x_1 x_2]-5x_1 x_2`
`<=>Q=-3[(2m-2)^2-2.(-3)]-5.(-3)`
`<=>Q=-3(2m-2)^2-18+15`
`<=>Q=-3(2m-2)^2-3`
Vì `-3(2m-2)^2 <= 0<=>-3(2m-2)^2-3 <= -3 AA m`
`=>Q <= -3 AA m`
Dấu "`=`" xảy ra `<=>2m-2=0<=>m=1`
Vậy GTLN của `Q` là `-3` khi `m=1`