Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

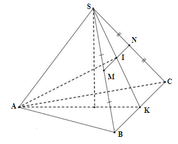
Ta có: S A ⊥ A B ; S A ⊥ A C ; B C ⊥ A B ; B C ⊥ S A
Suy ra, B C ⊥ S A B nên: B C ⊥ S B
Do đó, tứ diện S.ABC có 4 mặt đều là các tam giác vuông.
Ta có: AB là hình chiếu của SB lên (ABC) nên S B A ^ = 60 o
tan S B A ^ = S A A B ⇒ A B = S A tan S B O ^ = a 3 3 = a = B C A C = A B 2 + B C 2 = a 2 + a 2 = a 2 S B = S A 2 + A B 2 = a 3 3 + a 2 = 2 a
Do đó ta có
S t p = S S A B + S S B C + S S A C + S A B C = 1 2 S A . A B + S B . B C + S A . A C + A B . B C = 1 2 a 3 . a + 2 a . a + a 3 . a 2 + a . a = 3 + 3 + 6 2 a 2
Vậy S t p = 3 + 3 + 6 2 a 2
Đáp án A

Đáp án A

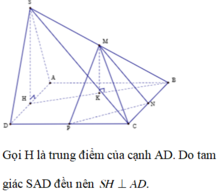
+ Do các cạnh bên cùng tạo với đáy một góc bằng nhau nên hình chiếu vuông góc của S trên mặt đáy trùng với tâm đường tròn ngoại tiếp tam giác ABC.
+ Mà tam giác ABC vuông tại B nên trung điểm H của AC chính là hình chiếu vuông góc của S trên mặt đáy ⇒ SH ⊥ ABC .
Góc giữa SA và mặt đáy chính là góc giữa SA và AC hay SAC ⏜ = 60 °
⇒ ΔSAC đều => Trọng tâm G chính là tâm đường tròn ngoại tiếp tam giác SAC và G ∈ SH .


Đáp án D
Gọi độ dài một cạnh góc vuông của tam giác vuông là 
Khi đó độ dài cạnh huyền là a−x.
Độ dài cạnh góc vuông còn lại của tam giác vuông là ![]()
Ta có diện tích tam giác vuông ![]()

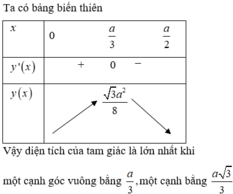
Ta có bảng biến thiên
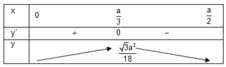
Vậy diện tích của tam giác là lớn nhất khi một cạnh góc vuông bằng
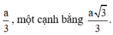

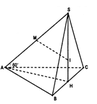

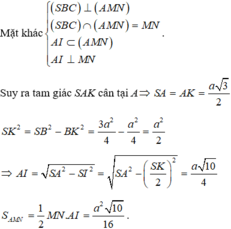







Lời giải:
Diện tích tam giác là: $9\times 6:2=27$ (cm2)
_ _ --- p